Epi - Lecture 4 - Critical appraisal 1 - 16/01

critical appraisal

• assessment of scientific evidence by reviewing its value, relevance, validity and results to specific situations/contexts

  • balanced assessment of strengths and weaknesses of any study

  • ensure studies of peers are valid and credible.

• it is not → negative critique and dismissal of research, based entirely on the assessment of statistical analyses and results.

explain distribution, determinants and application in epidemiological studies

• distribution → compare frequencies, incidence, prevalence

• determinants → assess relationship/association between exposure and outcome

• application → to generate reliable and valid evidence for use in specific populations.

What is validity

• Validity refers to how well a test, measurement, or study accurately represents what it is supposed to measure

different kinds of validity in critical appraisal

• Internal validity = assesses whether a study accurately establishes a cause and effect relationship between variables.

• External validity = extent to which results from a study can be applied (generalized) to other situations, groups or events

• Content validity = evaluates whether a test covers al relevant aspects of the concept being assessed.

• Construct validity = does the test measure the concept it intended to measure

• Cross-cultural validity = determines whether a study applies equally across different cultures and societies.

validity versus reliability

• validity is about whether you measure what you want to measure, reliability is about getting consistent outcomes

• BUT, sometimes you get the wrong results multiple times, while it is still not valid → therefore, cannot only focus on reliability.

reliability assessment

• Cronbach alpha (α) = assesses internal consistency / reliability of a study

• → gives a value of 0 to 1 → when α > 0.7 it is reliable.

type 1 versus type 2 error

• type I error (α) = reject the H0 , while in reality it is true

  • you’re pregnant → said to 80 year old man

• type 2 error = maintain the H0 , while in reality it is false

  • you’re are not pregnant → said to obvious pregnant lady

• type 2 error is worse!

• p value < 0.05 → less than a 5% probability that H0 is correct

statistical power

• statistical power → the probability of not making a type II error → the ‘power’ to detect an existing difference in the population

• 1 – α = maintaining H0 , because it is true

• 1 – β = rejecting H0 , because it is false.

what is probability sampling

• selection of sample using randomization

4 different probability sampling types

• Simple random sample → select samples from a given population and everyone has an equal chance of being selected.

• Stratified random sample → stratify into subpopulation or subgroups based on gender, age or other factors, then randomly select samples.

• Cluster sample → random sampling of clusters/subpopulations → cities, districts, towns, villages.

• stage / multistage sample → researchers select samples in multiple stages (large, geographical populations). population is divided in groups / clusters. Then random selection from these groups.

3 different non-probability sampling types

• Purposive → select sample purposely based on expertise or reliable judgment.

• Convenience → select the most easily accessible sample.

• Snowball → hard to access population, recruit participants via other participants.

descriptive statistics

• Summarize the data of the sample, identify patterns and generate a hypothesis → types of data descriptive statistics:

  • categorical (gender, age group, marital status) →

    • measures of frequency (= number of instances in a group).

  • continuous/numerical (age, blood pressure values).

    • measures of central tendency; mean, median, mode

    • measures of dispersion; range, inter-quartile range, and median from lower half - variance (σ²) (average of squared deviations of individual scores from the mean) - standard deviation (σ) (square root of the variance, tells you how dispersed data is in relation to mean -> the lower the SD, the better your data).

inferential statistics

• draw conclusions about the population, distinguish true differences from random variation → hypothesis testing

• important to look into distribution

  • normal distribution = some data approximates a normal/bell curve

difference between parametric and non-parametric tests

• Parametric tests: assumes the data are normally distributed → have to do normality tests; Kolmogorov-Smirnov test (sample size > 50), Shapiro-Wilk test (sample size < 50), normality plots (histogram).

• Non-Parametric tests: does not need normally distributed data (when parametric tests don’t work) → distribution-free → Wilcoxon-signed rank/Mann-whitney U test.

when to use which test

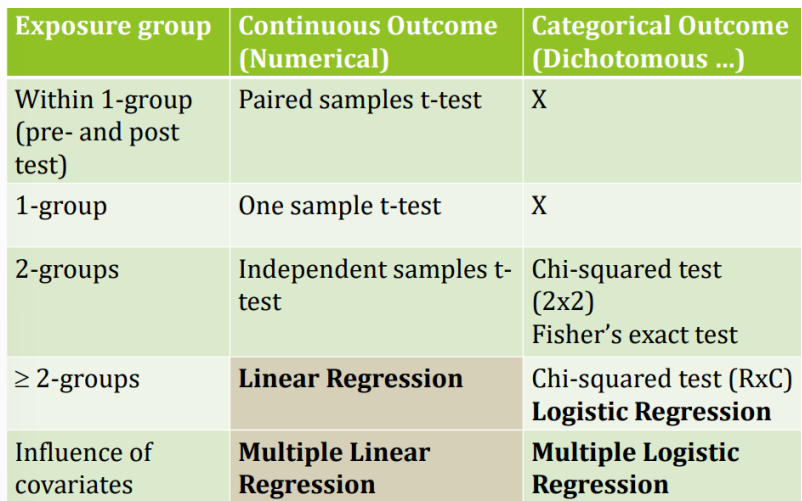
effect size

• used a lot more these days that P values

• shows how strong the relationship is and in which direction, positive or negative (P value only shows IF there is a relationship)

common effect sizes - Cohen’s d

• Cohen's d = indicates the difference between two means →

  • formula: (mean of experimental group - mean of control group) / standard deviation

  • → a value <0.2 indicates a small effect

common effect sizes - correlation coefficient

• Correlation coefficient (r) = measures the strength of a linear association between two continuous variables → the closeness with which points lie along the regression line → r lies between -1 and +1 → if r = 1 or -1, there is perfect positive (1) or negative (-1) linear relationship → if r = 0, there is no linear relationship between the two variables

common effect sizes - beta coefficient

• Beta coefficient (b or β) = (linear regression) degree of change in the outcome variable for every 1-unit of change in the exposure variable → can be positive or negative → regression models also provide an R 2 = percent of variance in the outcome variable that is explained by the set of independent variables → better to go for (significant) standardised than unstandardised beta coefficients.

  • if b is positive: for every 1-unit increase in the exposure variable, the outcome variable will increase by the beta coefficient value.

  • If b is negative: for every 1-unit increase in the exposure variable, the outcome variable will decrease by the beta coefficient value.

common effect sizes - odds ratio and risk ratio

• Odds ratio and risk ratio = odds or risks of an outcome in exposed vs. non-exposed.

common effect sizes - 95% confidence interval

• 95% confidence interval = being 95% confident that the population mean falls within this range

  • if the value of (1) null is seen within the 95% CI (especially in case of OR and RR), then we know that the association is not statistically significant

  • an odds ratio of 5.2 with a CI of 3.2-7.2 suggests there is a 95% probability that the true odds ratio would be likely to lie in the range 3.2-7.2 → has to lie above 1 (the null value).