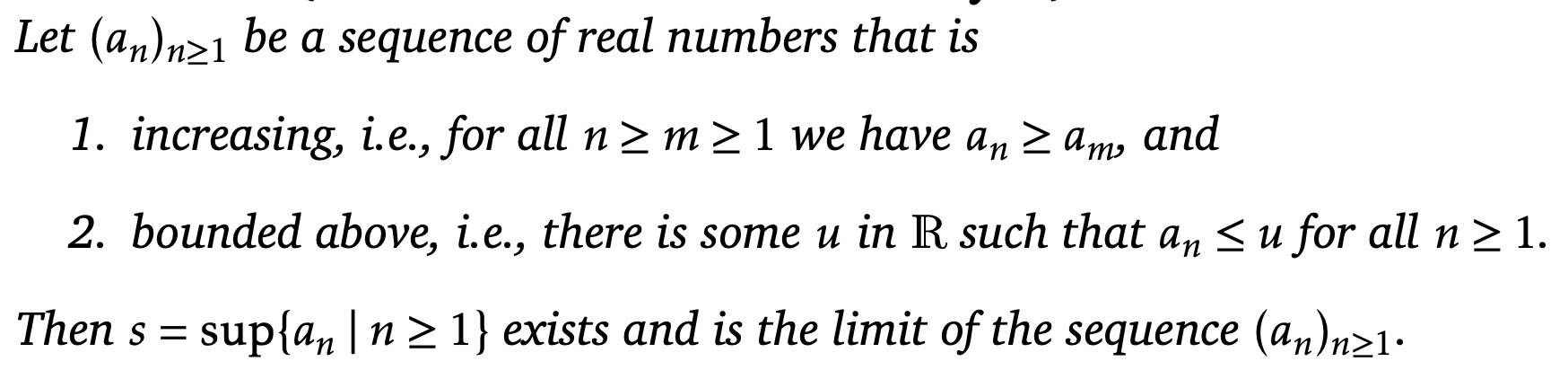Calculus: 5 - Sequences

define a binary relation over sets A and B

a subset of the Cartesian product A × B; that is, it is a set of ordered pairs (a,b) consisting of elements a in A and b in B

define n-ary relation over sets A1,...,An

a subset of the Cartesian product A1×...×An

what are examples of side effects of programmable functions

output text to the console, write a record to a database, send data over the network, etc.

define sequence

A sequence is a function f : N → R that maps natural numbers to real numbers. Often it is convenient to define a sequence as a function f : N+ → R that maps positive natural numbers to real numbers, which is the terminology we adopt.

define terms of sequences

outputs of f(n)

sequence notation

(an)n≥1, where an = f (n)

define arithmetic sequence

sum of an arithmetic sequence

Sn = n/2 ( a1 + an ) .

define geometric sequence

sum of a geometric sequence

Sn = a(1−r^n)/(1−r) if r /= 1

define Fibonacci sequence

definition of an increasing sequence

A sequence (an)n≥1 is increasing if an+1 ≥ an for all n ≥ 1

definition of a decreasing sequence

it is decreasing if an+1 ≤ an for all n ≥ 1.

define monotonic sequence

either increasing or decreasing

define sequence convergence to a limit

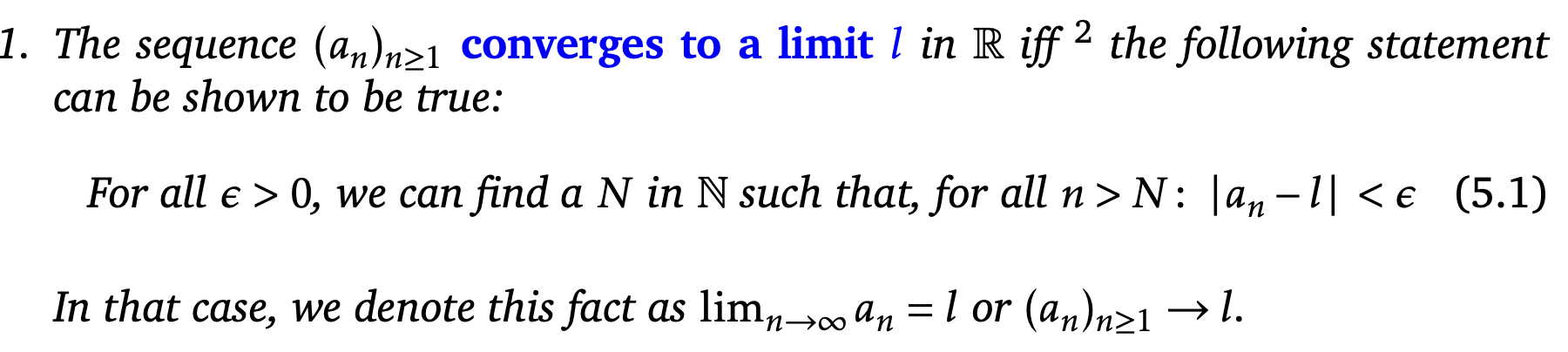
define sequence convergence to infinity

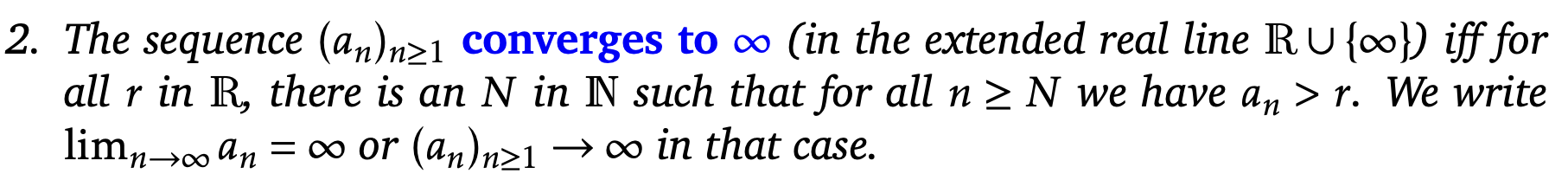
define sequence convergence to -infinity

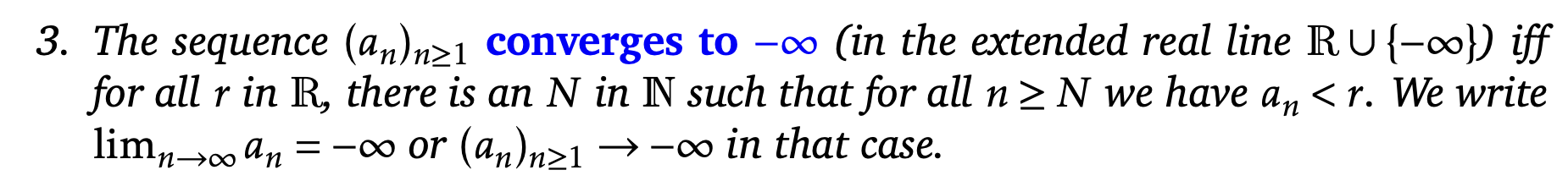
define sequence convergence

The sequence (an)n≥1 converges if it converges either to a real number or to ∞ or to −∞.

define sequence divergence

The sequence (an)n≥1 diverges if it does not converge

define the limit inequality

|an − l| < ε is called the limit inequality and says that the distance from the nth term in the sequence to the limit should be less than ε.

common convergent sequences

combinations of sequences

Given sequences (an)n≥1 and (bn)n≥1 which converge to limits a ∈ R and b ∈ R respectively, and a real constant λ, we have

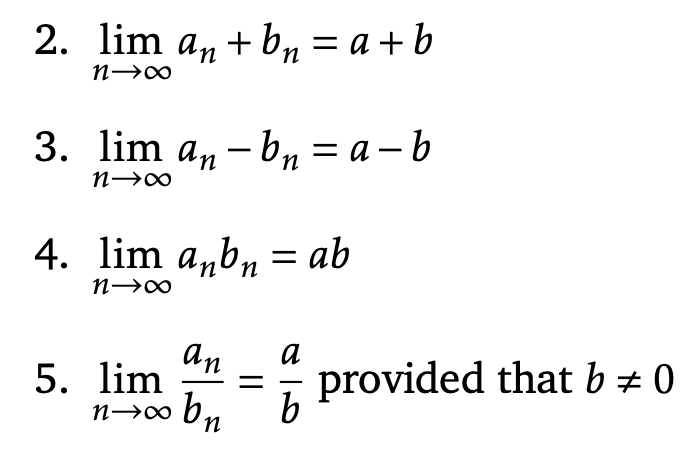
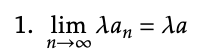
triangle inequality definition

|a+b|≤|a|+|b|

prove by squaring |a+b| and using algebraic manipulation

If (an)n≥1 converges to a ∈ R, is it bounded?

it is bounded

is limit of a sequence unique?

a sequence (an)n≥1 can only have one limit

define Cauchy sequence

A sequence (an)n≥1 is a Cauchy sequence iff for all ε > 0, there is some N in N such that for all n, m > N we have |an−am| < ε

A subset A ⊂ R is said to be complete if

any Cauchy sequence in A converges to a limit in A

define the sandwich theorem

Define the ratio test for sequences

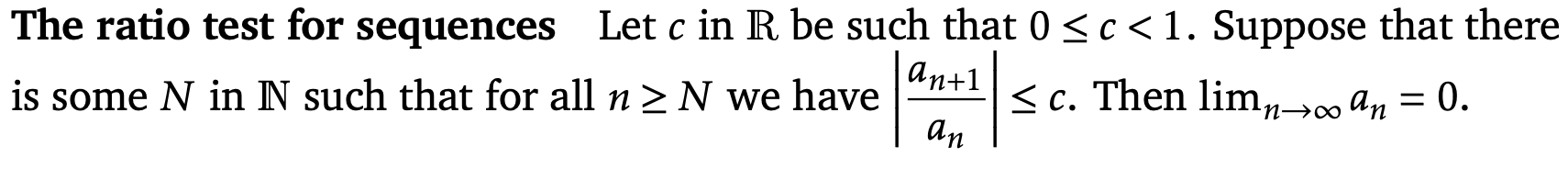
Define the limit ratio test

Define subsequence

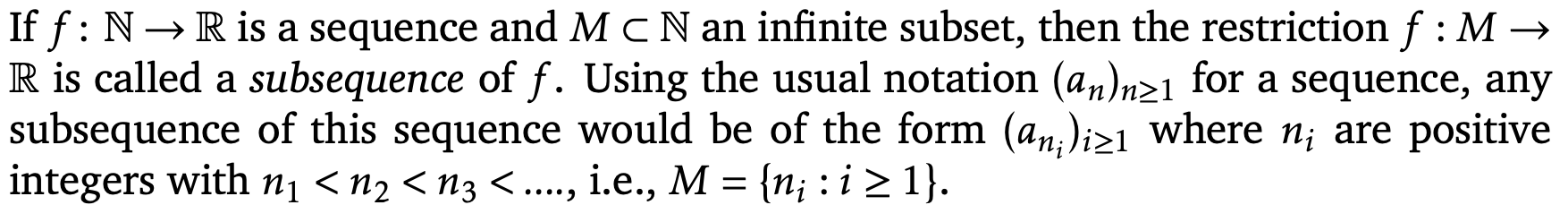
Any subsequence of a convergent sequence converges to…

…the limit of the sequence

define a peak of a sequence

Consider a sequence (an)n≥1. For any m ≥ 1, we say that am is a peak of (an)n≥1 if am ≥ an for all n ≥ m

useful techniques for manipulating absolute values

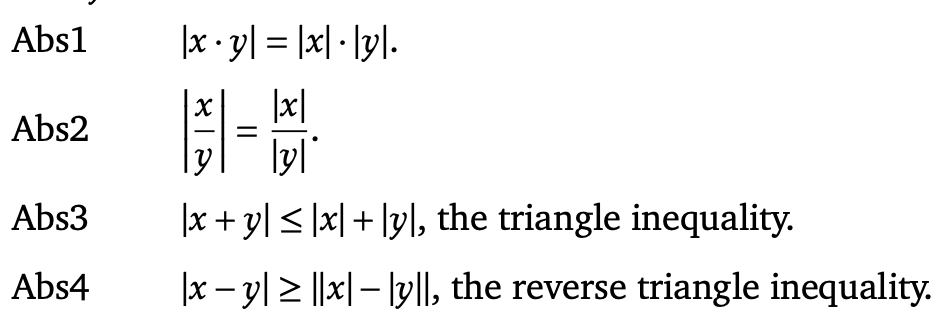
define upper bound

u is an upper bound of X if x ≤ u for all x ∈X

define lower bound

l is a lower bound of X if l ≤ x for all x ∈ X

define supremum/least upper bound

a least upper bound (supremum, sup(X)) of X is an upper bound s of X such that s ≤ u for all upper bounds u of X

define infimum/greatest lower bound

a greatest lower bound (infimum, inf(X)) of X is a lower bound i of X such that l ≤ i for all lower bounds l of X

a set X is bounded above if

if X has an upper bound

a set X is bounded below if

if X has a lower bound

Axiom of Dedekind-completeness for real numbers

Every nonempty subset X of the real numbers R that is bounded above has a least upper bound

Fundamental theorem of analysis