Legal Reasoning Quiz 1

Soundness

An argument is sound if its valid and it has true premises

Cogent

An Argument is cogent if it is strong and has true premises

Premise

A premise is made up of propositions ( a statement that can either be true or false)

Validity

An argument is valid when the conclusion folows typically from the premises

Strenth

The More Support there is for the conclusion (More evidence, more cases, more explanations) ; The stronger an inductive argument will be

Deductive Argument

• An Attempt to prove a conclusion with 100% certainty

• If Premises = True; conclusion must be true.

Inductive argument

• Is ampliative reasoning from cases:

• The premises do not 100% guaruntee the truth of the conclusion.

What defines an Argument

an Argument = an attempt to prove/convince others of something
An argument always has conclusion + Premises

What defines a set of facts

A set of facts merely provides Info

Premise indicator words

• Since

• Because

• As

• For

• Given that

• Assuming That

• The reason that

• the view of the fact that

Conclusion Indicator words

• Therefore

• Thus

• So

• As a Result

• consequently

• it follows that

• hence

• which means that

• Which implies that

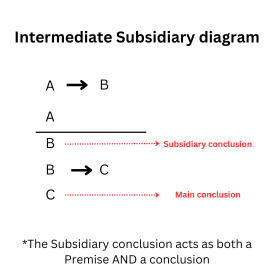
Intermediate subsidiary conclusion

They are premises that both have premises that support them and in turn provide support for the main conclusion of the argument.

Background Information

• Adds context to an argument, but is not itself a part of that argument

• Not shown on any diagram.

• Its not supported by any premises

• It does not provide support for any conclusions

A conditional statement

a basic logical relationship between two propositions telling us that if the one condition is met, then another condition must be met.

How to find the contrapositive

You reverse the order of the sufficient and necessary conditions, and then you negate both sides.

A→ B then becomes [ ~B→~A]

The rule of “IF”

IF always introduces the sufficient condition

The rule of “ONLY IF/ONLY WHEN/ONLY WHERE”

ONLY IF introduces the necessary condition.

The Rule of “UNLESS/EXCEPT WHEN”

UNLESS introduces the necessary condition but you need to negate the other side (sufficient condition)

The Rule of “ALL”

All refers to the sufficient condition, the other part of the proposition is the necessary condition

The rule of “NO/NOWHERE”

NO introduces the sufficient conditon, but you need to NEGATE the other side.

Contrapositive AND/OR rule

When doing the contrapositive for a conditional statement you need to replace and with or and vice-versa

Define “SOME”

Some is defined as minimum of at least one member of a group, but it could refer to as many as all members of the group ( 1 or more members of a group?)

what’s an example of a SOME statement?

“ Some x’s are Y’s

How would you diagram a SOME statement?

X Some Y (with a biconditional arrow on top)

What does it mean when it says that a SOME statement can commute?

Some statements COMMUTE, meaning you can swap the position of X and Y: If some X’s are Y’s, then we also know that some Y’s are X’s.

The rule of “FEW SEVERAL MANY”

• Few and several are defined as 3 or more; Many is a “large number”

• But they all give us very little information! Who knows how much of a group they make up.

• So, we translate all of them as SOME statements.

Define MOST

MOST is defined as greater than 50% of a given group

How to diagram the MOST statement

We will diagram “Most P’s are Q’s” as:
PMost^→ Q (arrow above the word Most)

Do most statements commute (meaning biconditional)?

NO!

Can you make a valid inference from two SOME statements?

No you cant, its invalid.

Can you make a valid inference from a SOME and a MOST statement?

No you cant, it’s invalid.

Can you make a valid inference from two MOST statements?

Yes, but only in one case: when the two statements both tell you about most of the same group

The ‘MOST’ form of valid inference

• Most A’s are B’s

• Most A’s are C’s

• So it follows that SOME B’s are C’s

Can you make a valid argument with a SOME/MOST statement and a regular conditional statement?

YES SOMETIMES… if that conditional statement is talking about entire groups (all/no/only if/unless, etc)

To Draw an inference in such a case, the term linking the two statements must be a sufficient condition in the unqualified conditional statement or it’s contrapositive.

Does deductive deal with soundness or cogency?

Soundness

Does Inductive deal with soundness or cogency?

Cogency

What makes a good deductive Argument?

A good deductive argument is both Valid and Sound.

What makes a good inductive argument?

A good inductive argument is both strong and cogent.