BIPN 100 Lecture #2 Terms - Nervous System Physiology II: Passive Membrane Properties

Semipermiable

ions must cross membrane via ion channels

Ions

molecules w/ a net electrical charge

Ion Channels

membrane proteins w/ selective permeability for particular ions

Leak Channels

pores that remain open

Voltage-gated ion channels

open/close in response to changes in membrane potential

Ligand-gated ion channels

open in response to chemical signals binding

Membrane Potential (Vm)

difference in electrical charge between inside and outside of cell

voltage measured as relative differences between in/outside

Electrophysiology

method to measure membrane potential

Vm = V inside - V outside

• a recording electrode is inserted into neuron

Resting Membrane Potential (RMP, V rest)

Vm when a cell is at rest, not firing an action potential

• steady state: no net movement of charge

• Around -50 to -70 mV

Sodium-potassium pump

3 Na+ out, 2 K+ in

builds up Na+ in ECF, K+ in ICF

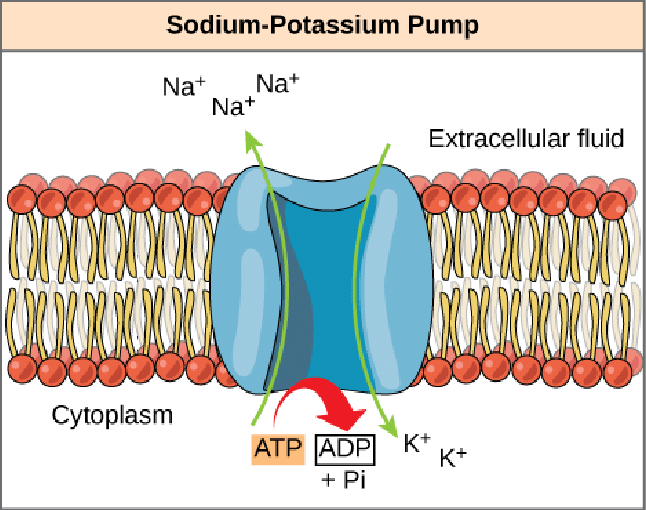
Antiport

carrier protein that moves substances in opposite directions

Active Transport

Na+-K+-ATPase hydrolyzes ATP to move ions against concentration gradient

What are 2 factors that determine Vm

1. Electrochemical Gradient

2. Differences in membrane permeability— ability for ions to pass through membrane

Electrochemical Gradient

uneven distribution of ions across cell membrane

Electrical Driving Force

Attraction and repulsion between charged particles

Chemical Driving Force

diffusion, drives ions from region of high to low

At rest, what is the membrane more permeable to and why?

The membrane is more permeable to K+ because #K+ leak channels > #Na leak channels

Equilibrium Potential (E ion)

membrane potential that exactly opposes concentration gradient

• electrical & chemical forces are equal and opposite

• no net movement of ions

Nernst Equation

Calculates equilibrium potential for a membrane permeable to one ion

• z = ion charge

• [ion] out = concentration of ion in ECF

• [ion] in = concentration of ion in ICF

Calculating F ion

Driving forces on an ion are dependent on the difference between Vm and E ion

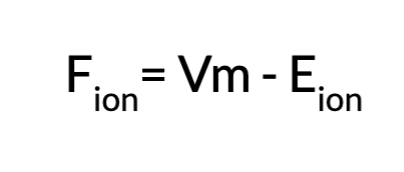
Goldman-Hodgkin-Katz (GHK) Equation

calculates membrane potential resulting from contribution of E ions of all ions as a function of permeability

• permeability = ion contribution to membrane potential

Electrical Current (I)

flow of electrical charge carried by an ion

1. measured in amperes (amps)

2. ion movement produces electrical signals

3. I dependent on F ion and permeability

Conductance (G)

ease with which ions flow across membrane

• units: siemens

• conductance determined by # open ion channels

• stimuli alter permeability —> ions flow w/ electrochemical forces

Resistance (R)

force that opposes flow

• inverse of conductance (1/G)

• Units: Ohms (omega)

• in neurons:

  • membrane resistance (Rm)

  • cytoplasm resistance (Ri)

Ohm’s Law

states that current flow is directly proportional to electrical potential difference between 2 points and conductance

• small changes in [ion] —> big changes to membrane potential

Depolarization

increase in Vm

• membrane becomes more permeable to Na+

• inward I Na+ w/ electrochemical gradient

• Vm above RMP

Hyperpolarization

decrease in Vm

• membrane becomes more permeable to K+

• outward I K+ w/ electrochemical gradient or inward I Cl-

• Vm below RMP