Multiphase Systems Equations and meaning

These flash cards will represent all equations I must learn + ones that are given but I must know the content around them and what they mean.

What gas law equation can we use to relate density to pressure and temperature? Manipulate it to make density the subject.

Ideal gas law pV =nRT, manipulated to 𝜌 = P/RT (To manipulate it must know moles = mass/molar mass and that density (𝜌) is mass/volume.

What is sonic velocity and what is the equation for it? Can you define Mach number and write the equation for it.

Sonic velocity is the maximum speed a pressure change can propagate through a compressible fluid which is given by u_s= ( 𝛾𝑅𝑇 )^0.5 where 𝛾 is the specific heat ratio, R is the specific gas constant, and T is the absolute temperature. 𝛾 = C_p / C_v . Mach number is the ratio of the speed of a fluid and the sonic velocity of the same fluid, M = u/u_s where u is the velocity of the fluid and u_s is the sonic velocity.

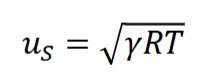
What does stagnation pressure / temperature mean? Where does it come from and what are the equations?

Stagnation properties are the value of the property if the fluid has brought to rest. It is the sum of the static and the dynamic values. Pressure for example is derived from Bernoulli equation : P + 𝜌u²/2 𝜌gz = constant Where P is the static pressure and 𝜌u²/2 is the dynamic pressure. The equations are given in the images below. P_o is the stagnation pressure. M is Mach number. 𝛾 is specific heat ratio.

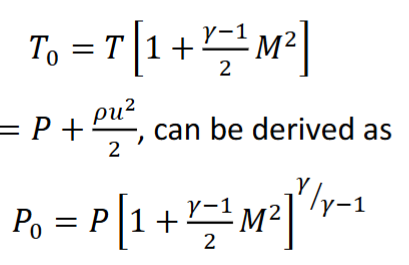
What is choked flow? When is the maximum mass flow rate and why? What are the equations for the choked mass flow rate and the critical pressure ratio and why is the critical pressure ratio significant?

Choked flow is when the flow rate through a restriction (nozzle) is at it’s maximum. This occurs when the Mach number is 1 which is when the fluid is traveling at sonic velocity. The critical pressure ratio is significant because it shows when a flow will be choked. It is the ratio of the Pressure at the restriction / the Pressure just before the restriction.

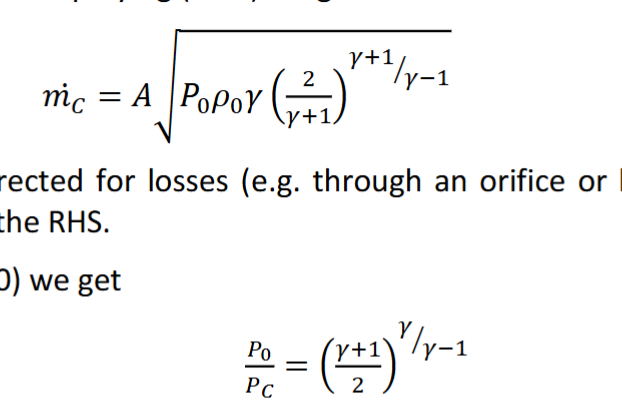
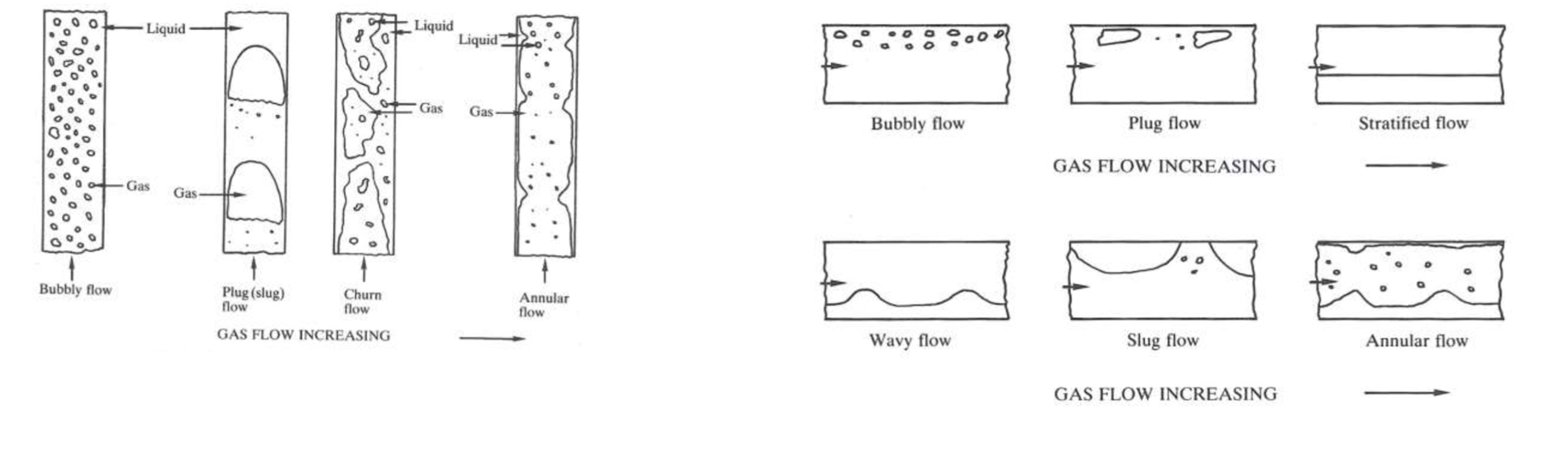
What are the different types of two phase flow patterns for horizontal and vertical flow respectively?

Horizontal flows are different as gravity is acting perpendicular to the flow of fluids.

Basic definitions: Show the equations for Mass flux

mass is mass and flux is per m squared, donation for mass flux is G

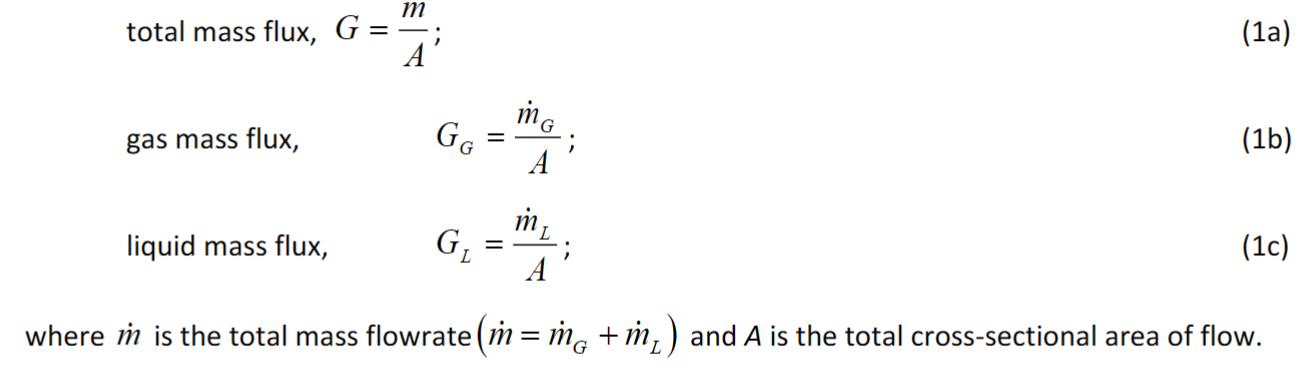
Basic definitions: Show the equations for Quality and dryness

Quality is how much the flow is gas (as a mass flow) because it originates from steam power plants and we want the gas and not the shitty water.

Basic definitions: Show the equations for Void fraction and superficial phase velocities and explain what they are. From this what are the actual phase velocities?

Using the void fraction and the superficial phase velocities, it can be shown that the actual phase velocities are: U_g = U_gs/a , U_L = U_Ls/a

What are flow pattern maps?

Flow pattern maps are graphs that show regions for correspond to each type of flow. The Hewitt and Roberts (1969) map applies to vertical upflow in a tube. The Taitel and Dukler (1976) map applies to horizontal flow in a tube. Image shows equations for Taitel and Dukler.

What is the generalised equation for pressure drop in a pipe? From this derivation, derive the frictional pressure gradient in terms of friction factor.

As shown in image. friction factor f = 𝜏/(0.5*𝜌*u²) sub into frictional pressure gradient to get -(dp/dz)_f = 4f𝜌u²/2d = 4fG²/2𝜌d. For turbulent flow f = 0.079 Re^-0.25 , Re = 𝜌ud/𝜇. For laminar flow, f = 64/Re.

Write the equations for mixture density homogeneous density, void fraction (in terms of densities and quality), homogeneous void fraction, homogenous density and homogeneous viscosity. (HINT: one you have the homogeneous void fraction equation you can sub it into the homogeneous density equation to get the homogeneous density in terms of quality and the homogenous viscosity is the same as the homogeneous density just all density terms replaced with viscosity.

What is the homogeneous frictional pressure drop and the homogeneous gravitational pressure drop. Show the Homogeneous Reynolds number.

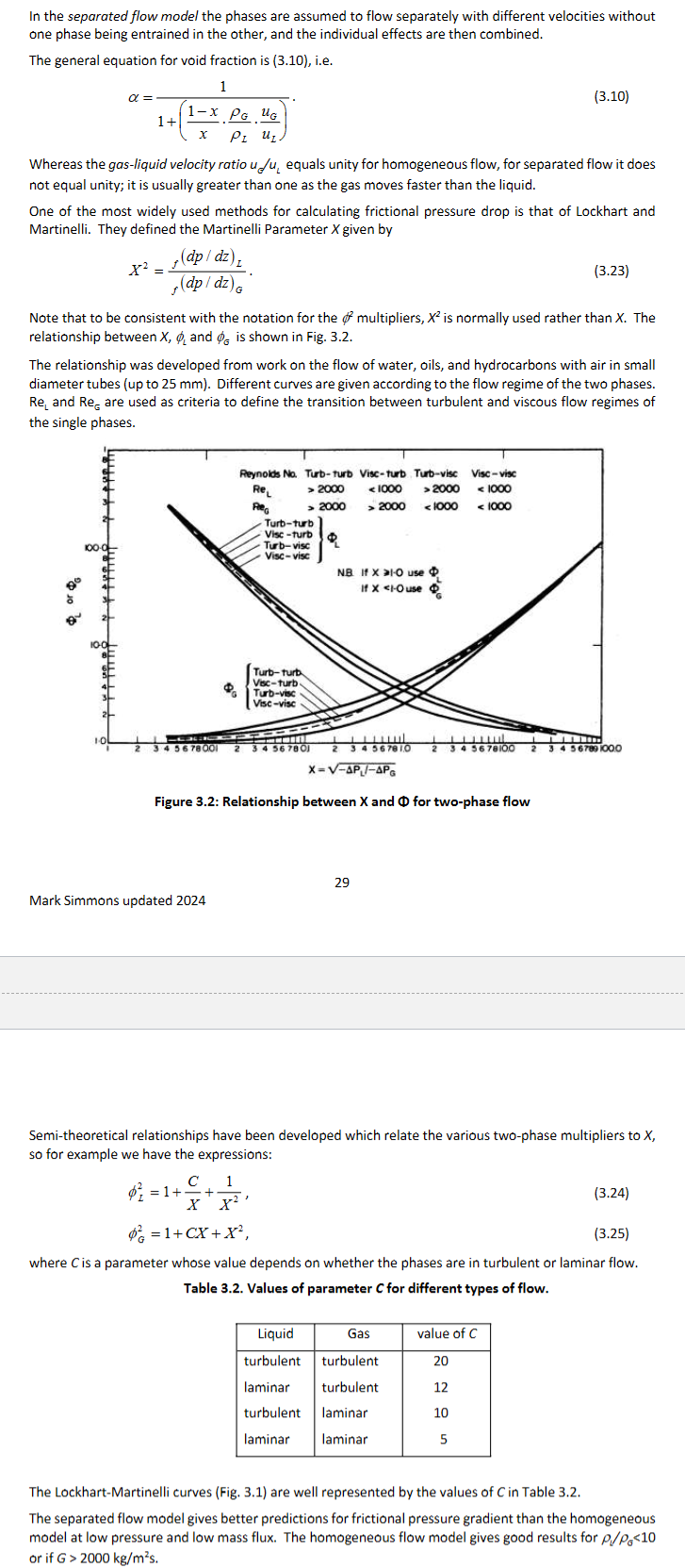
Explain what a Two-Phase multiplier is. Show the equations for the 4 main types of two phase multipliers and explain what each are. Why are 2 of them more useful than the others? (HINT : check boundary conditions when x = 0 and x = 1 and what they depend on).

Explain the difference between the separated flow model and the homogeneous flow model, how it related to 2 of the two phase multipliers and how you would use it to solve the frictional pressure drop. When would you use the homogeneous flow model?

What are the 3 boiling types (mechanisms) and what are the two main conditions that these can occur in? Show Newton’s law of cooling with regards to the saturation temperature. What is latent heat?

Latent heat is the energy required to change the state of a material.

What is the Nusselt number, the Prandtl number and the Reynolds number? What is the full form of the correlation? What are the common values of n and m? What is C_sf

The Nusselt number is a dimensionless number representing the ratio of convective to conductive heat transfer. The full form of the correlation is Nu = f(Re, Pr), indicating that the Nusselt number is a function of the Reynolds and Prandtl numbers. Nu = hL/k ,

h is the convective heat transfer coefficient. 

L is a characteristic length scale (e.g., diameter of a pipe, length of a flat plate). 

k is the thermal conductivity of the fluid. 

Pr = (ν/α) = (μ * cp) / k where:

• ν (or η) is the kinematic viscosity (momentum diffusivity). 

• α is the thermal diffusivity. 

• μ is the dynamic viscosity. 

• cp is the specific heat capacity at constant pressure. 

• k is the thermal conductivity. 

n = 0.33 and m = 0.7

C_sf is the surface fluid constant which depends on the surface and the fluid.

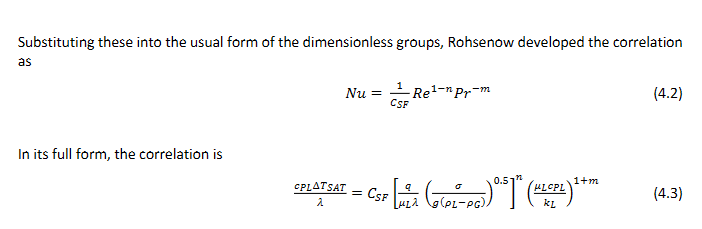
What is critical heat flux? What two steps become unstable causing CHF to be reached? Please show as a diagram. What is the final equation for CHF for a plate geometry?

Critical heat flux (CHF) is the maximum heat flux at which a coolant can remove heat from a surface before a significant reduction in heat transfer occurs, often leading to boiling crisis. The two steps that become unstable are the formation of vapor bubbles and the transition from stable to unstable liquid flow, which can cause the coolant to fail to contact the heated surface.

For pool boiling what are the equations for the CHF on cylinders and what are the heat transfer coefficients for film boiling in this scenario? What difference to the heat flux is made if the fluid is flowing?

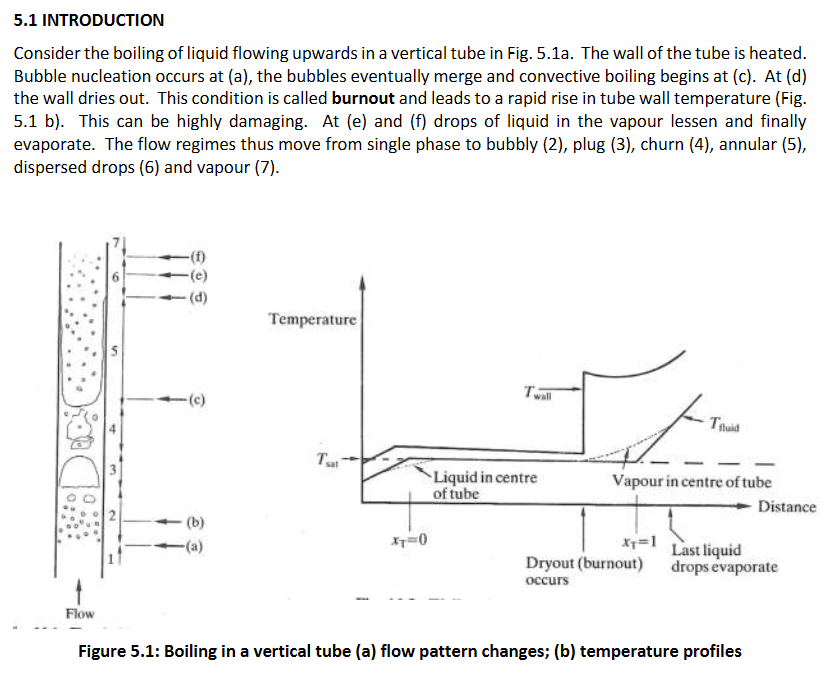
Water is flowing up a vertical pipe with heated walls, draw a visual diagram and a graph showing the temperature vs distance in pipe. When is burnout and what is burnout? What happens to the wall temp during burnout and why?

With respect to flow boiling, what is the equation for the thermodynamic quality of the mixture and can you draw a graph showing the heat transfer coefficient vs quality for different heat fluxes to show the points at which burnout will occur. What does this graph tell us?

The graph tells us that if the heat transfer coefficient is too high, burnout will occur before any vapour is formed. This is because the wall temperature is too high. Film boiling occurs as soon as the fluid enters the pipe causing the heat transfer coefficient to drop drastically causing the wall temperature to rise rapidly and damaging the boiler.

When does the onset of nucleate boiling occur and derive the equation?

What are the two mechanisms of boiling in flow boiling (not film because that would be burn out)? Explain the Chen method for finding the overall boiling heat transfer coefficient.

There are assumed to be two mechanisms at play in flow boiling
(a) Nucleate boiling, where bubbles form on the solid surface. If the liquid is subcooled these bubbles
collapse in the bulk and transfer their latent heat to heat up the liquid to its saturation temperature
(b) Convective boiling, where heat is transferred by conduction and convection through the liquid film on
the wall and evaporation happens at the liquid-vapour interface. Depending on the flow pattern, the
interface topology may be simple or complex. In annular flow, the process is further complicated by
transfer of heat and momentum between the liquid film, gas core and droplets in the gas core.
Burnout is generally to be avoided, as the rise in wall temperature can weaken or buckle the boiler tubes.
If the boiler happens to be a nuclear reactor, then the whole world will have a bad day.

Chen Method:

The overall heat transfer coefficient is the sum of the nucleate and convective heat transfer components. h_B = h_NB + h_FC where h_NB = S h_FZ and h_FC = F h_L .

h_FZ is found from the Forster-Zuber equation which is a very big correlation. ΔΔP_𝑆𝐴𝑇 is the difference in saturation pressure corresponding to Δ𝑇_𝑆𝐴𝑇. Find one and work out the other by relating using a thermodynamic gas law like pV =nRT.

h_L is the liquid heat transfer coefficient and is found using the Nusselt number formula and the Dittus-Boelter equation. Respectively Nu = (h * D) / k , Nu = 0.023 Re ^ 0.8 Pr ^ 0.4.

F is calculated from the Martinelli Parameter (X).

Then the liquid Reynolds number is calculated, 𝑅𝑒_𝐿 = 𝐺(1−𝑥)𝑑/𝜇_𝐿 and then used to calculate Re_TP = Re_LF^1.25 then, Re_TPR = 10^-4Re_TP.

Finally, the critical heat flux can be calculated to check that the flowing fluid will not achieve burnout using a final equation 𝑞_𝐶 = 𝑋𝐺(𝜆 + 𝐾Δℎ_𝑆), Where X and K are functions of three dimensionless groups, G is mass flux, λ is latent heat and Δℎ_𝑆 is the
inlet subcooling (J kg-1)

This card is to let you know that you are actively ignoring the Brownian motion derivation. But can you explain what it is in terms of a colloidal system? But what equation is important to remember? (the relationship between root mean squared displacement and diffusivity)

(𝑥̄ ²)^1/2 = (2𝐷𝑡)^1/2

What are intermolecular forces? Short range ____ forces and long range _____ forces (long range is van der Waals). What are the 3 van der Waals forces? How can this be written as a total energy potential? Then convert it to a force with respect to distance

Repulsive, attractive

Keesom (orientation) interactions which arise between polar molecules (permanent dipoles)
Debye (induction) interactions between a non-polar and polar molecule (induced dipole)
London (dispersion forces) occur in all atoms and molecules. They are much larger in magnitude
than the Keesom and Debye interactions for most colloid particles.

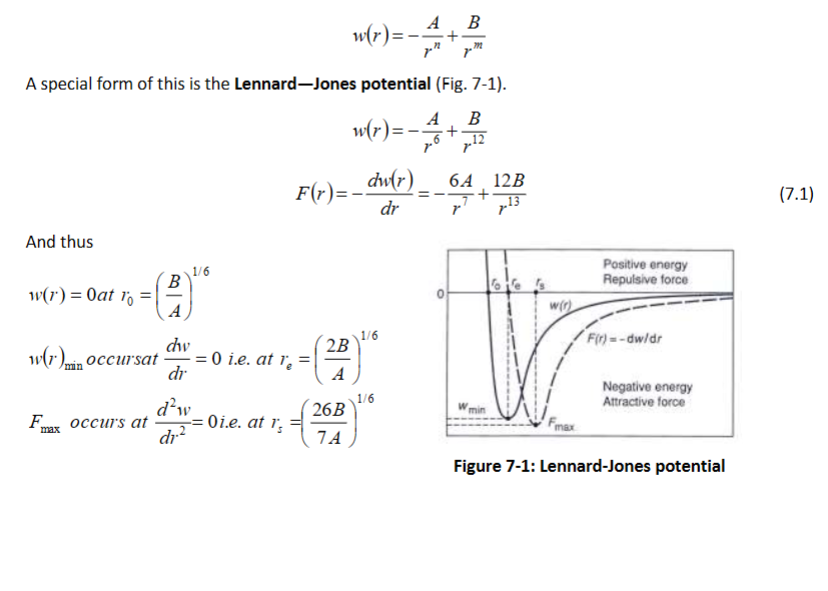
Explain Van Der Waals forces between 2 particles and derive the force from the energy of interaction. What is the Hamaker constant? What is the equation for the Hamaker constant? What would be the Hamaker constant for two identical particles (1) in a liquid (3)? Finally, for charged particles what is the Law convening the forces between them and what is the equation?

7.4 SURFACE CHARGING - ELECTRICAL DOUBLE-LAYER

7.5 ZETA POTENTIAL

I cba to make this flash card look through the notes chum