Gas Laws AP Chem

Gases:

uniformly fill any container

mix completely with any other gas

exert pressure on its surroundings

Standard conditions, 1 mol:

22.4 L at 0°C, and 1 atm

Pressure =

force / area

-molecules stricking an area on the wall

SI units

Newton/meter² = 1 Pascal (Pa)

1 standard atmosphere = 101,325 Pa

NOTE: difference between Pa and kPa

1 standard atmosphere = 1 atm = 760 mmHg = 760 torr

NOTE: these are on reference sheet (the important ones)

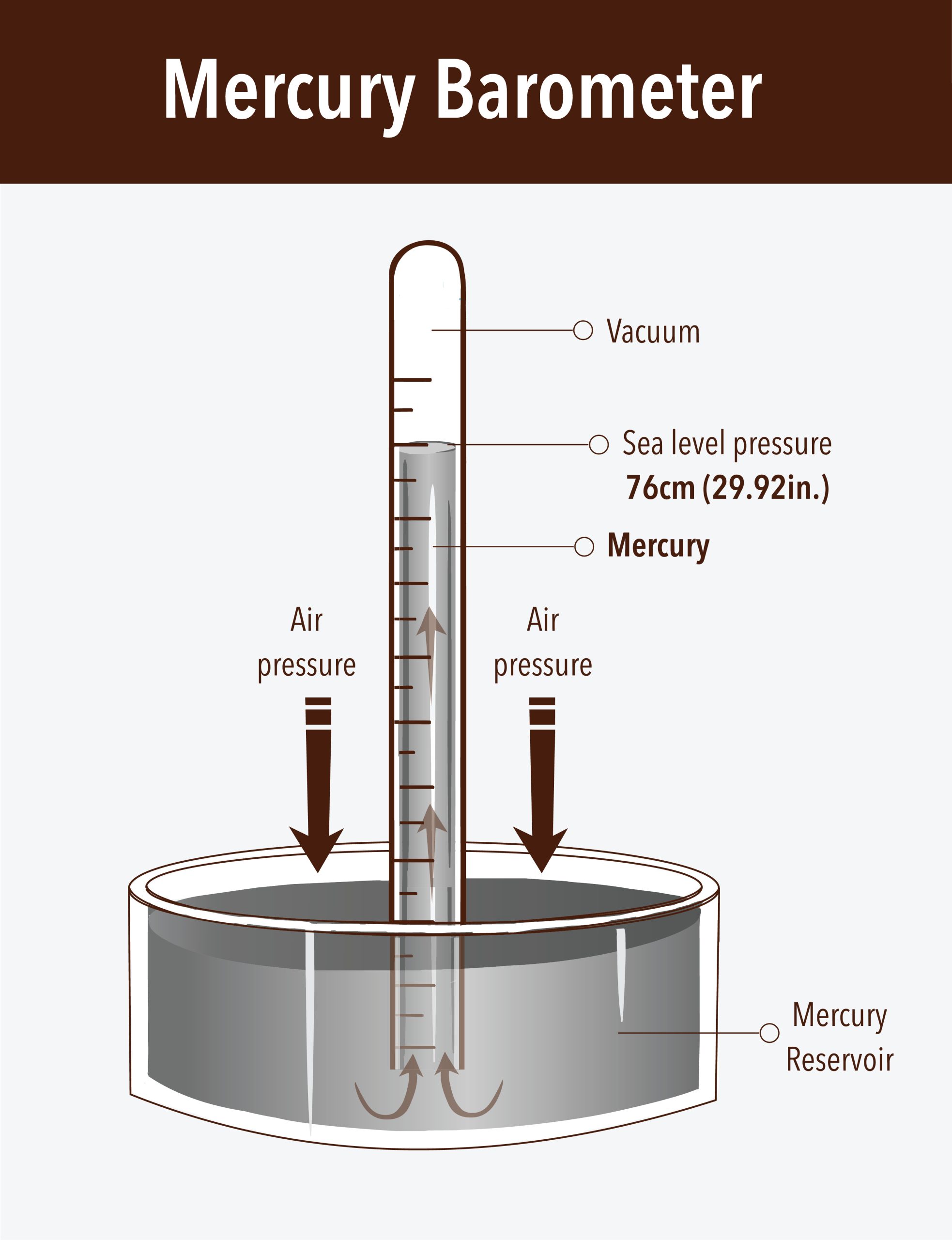
Mercury Barometer

-used to measure atmospheric pressure

-mercury flows out of the tube until the pressure of the column of mercury standing on the surface of the mercury is equal to the pressure of the air of the rest of the surface of mercury

(Honestly just look at the picture to understand)

Manometer

Device used for measuring the pressure of a gas in a container (lowkey unimportant)

Boyles Law

INVERSELY RELATED

Pressure and Volume

P1V1 = P2V2

only linear relationship

other variables MUST be held constant

Charles Law

DIRECT RELATIONSHIP

volume and temperature 

V1/T1 = V2/T2

V = bT (b is proportionally constant)

Temperature MUST be in Kelvin

(C + 273.15)

Avogadro’s Law

DIRECT RELATIONSHIP

Moles and Volumes are proportional

n1/v1 = n2/v2

V = an (a is a proportionality constant)

1 mol of any gas at STP = 22.4L

STP =  0C, 1 atm

Combined Gas Law

P1V1/T1 = P2V2/T2

Ideal Gas Law

All together

PV = nRT

R = universal gas constant 0.08206 (acheived by plugging in standard conditions) 

Molar volume of an Ideal Gas

1 mol of ideal gas at 0C and 1 atm, volume is 22.4L

Molar Mass of a gas

D = PM/RT

D= density g/L

M= molar mass g/mol

Daltons Law of Partial Pressure

Ptotal = P1 + P2 + P3 + …

-total pressure exerted is the sum of pressures of each gas would exert if it were alone

Non Ideal Gases, Postulate 3

Particles do not attract or repel

→ NOT common

Conditions that make a non-ideal gas

Pressure is high (Volume is low)

Temperature is low

Under these conditions:

-concentration of the gas particles is high

-IMFs can no longer be ignored

low temp. slows the particles down so they’re less likely to not attract or repel

Which gases deviate the least from ideality:

Lightest gases, and non polar gases

Strength order of IMFs:

1. Hydrogen Bond (H-N, H-O, H-F)

2. Dipole - Dipole (Polar molecules)

3. London Dispertion Forces (non polar molecules, more electrons = stronger LDF)

For a real gas actual pressure is …

lower than the pressure of an expected ideal gas

If gas patricles have IMFs…

pressure will be less than expected

The Measure of the speed of particles in a gas equation:

R = 8.3145 J/Kxmol (J = Joule = Kg x m² / s²)

T = temp of gas in K

M = molar mass of a mole of gas IN KILOGRAMS

final units in m/s

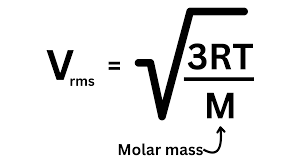
Calculating Average Kinetic Energy of a Gas:

1/2(RT)

R= 8.3145 J/Kmol

T= temp in K

final units in J/mol

rate of effusion equation

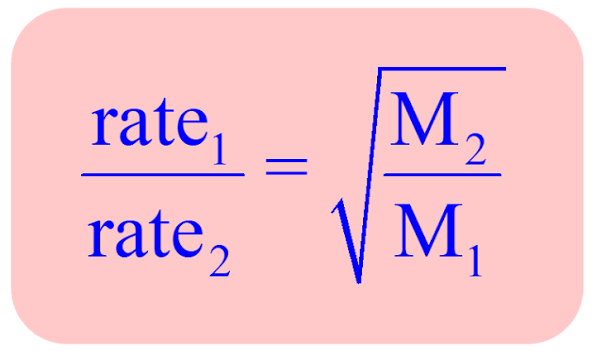
Conditions for ideality:

High temperature and low pressure

Which means there’s no IMFs so the gas molecules are insignificant

If it doesn’t behave ideally…

Pressure increases and volume of gas particles become significant

Pressure affects the volume since…

Now there’s a value in the container, because of the IMFs which clump particles together so now particles combine less

Kinetic Molecular Theory postulates:

1) gas particles are so small they’re negligible so volume of a gas particle can be ignored

2) gas particles are in constant motion, when the particles bump into the walls this results in pressure

3) particles are assumed to not attract or repel therefore IMFs can be ignored for an ideal gas

4) the avg KE is proportional to its kelvin temp: KE = 1/2mv²

Maxwell Boltzmann distribution:

Distribution of the kinetic energies of particles at a given temperature

Higher speed means less molecules sine there’s less collisions

(Spread your legs)

When you increase temperature..

Not every particle has the same KE, temp is the avg of the KE NOT its peak

Avg KE

Temp in Kelvin

1/2mv²

m: KILOGRAMS

KE: Joules

v: m/s

Velocity

Speed, m/s