Calc 2 Midterm JHU

List all the Series Tests

Basic Test for Divergence, p- series, geometric series, alternating series, telescoping series, limit comparison test, integral test, ratio test, root test, taylor series(test if x is in interval of convergence), absolute convergence

Basic Divergence test

a method to determine if a series diverges by checking if the limit of the terms approaches zero.

p-series test

if p is greater than 1 its converges if not it diverges

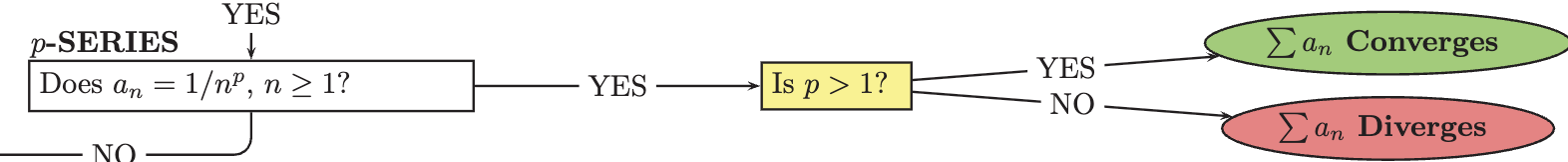
geometric series

a series of the form a + ar + ar² + ar³ + … which converges if the absolute value of the common ratio r is less than 1.

Alternating Series test

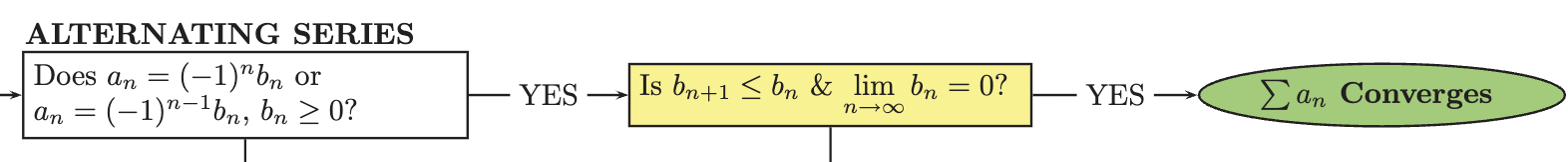
Taylor Series

Comparison test

A method for determining the convergence or divergence of a series by comparing it to another series whose convergence is known. If the series being tested is smaller than a convergent series, it also converges; if it is larger than a divergent series, it also diverges.

Limit Comparison Test

A method used to determine the convergence or divergence of a series by comparing it to another series with a known limit ratio as the terms approach infinity. If the limit exists and is positive, both series either converge or diverge together.

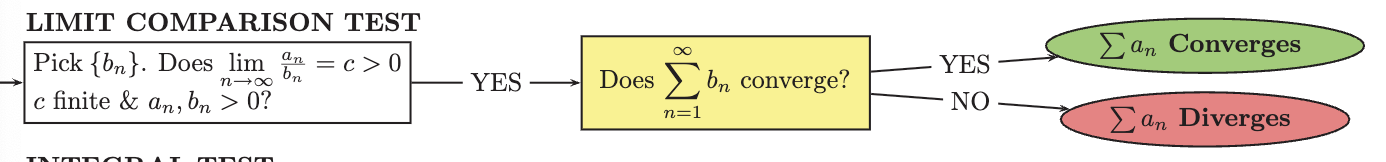
Integral Test

A method for determining the convergence or divergence of a series by evaluating the corresponding improper integral. If the integral converges, the series converges; if the integral diverges, the series diverges.

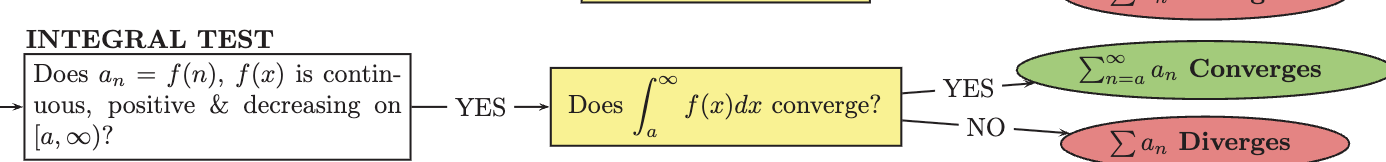
Ratio Test

A method used to determine the convergence or divergence of a series by examining the limit of the ratio of consecutive terms. If the limit is less than one, the series converges; if greater than one, it diverges; and if equal to one, the test is inconclusive.

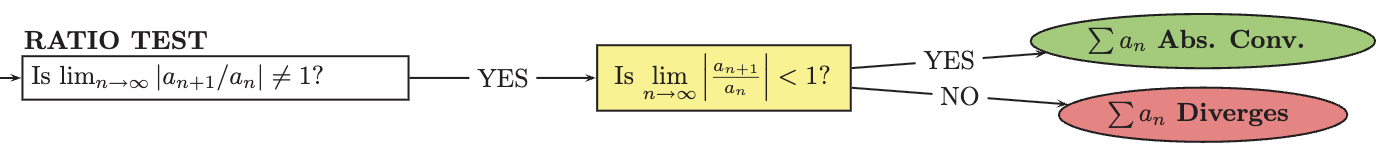
Root test

A method for determining the convergence or divergence of a series by taking the limit of the n-th root of the absolute value of its terms. If the limit is less than one, the series converges; if greater than one, it diverges; and if equal to one, the test is inconclusive.

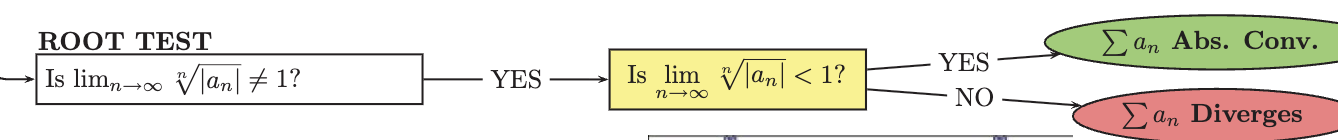
Absolute Convergence Test

A method to determine convergence by testing whether a series of absolute values converges. If the series of absolute values converges, then the original series also converges.

Geometric taylor Series

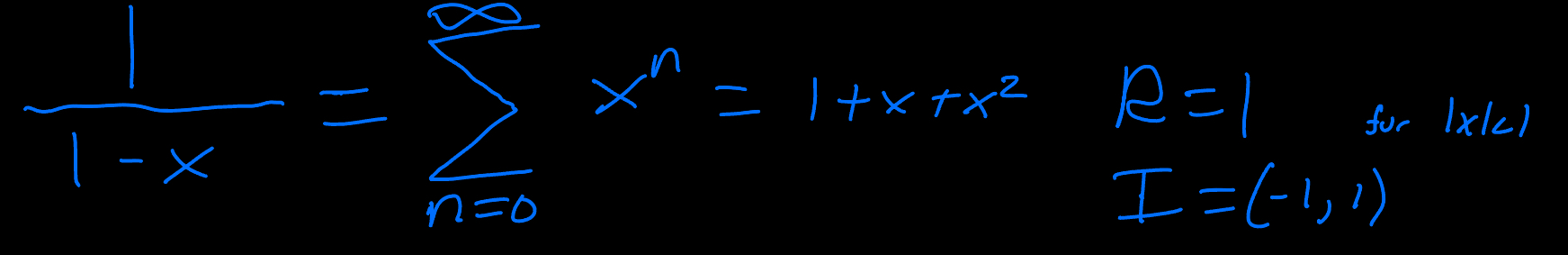
e^x Taylor Series

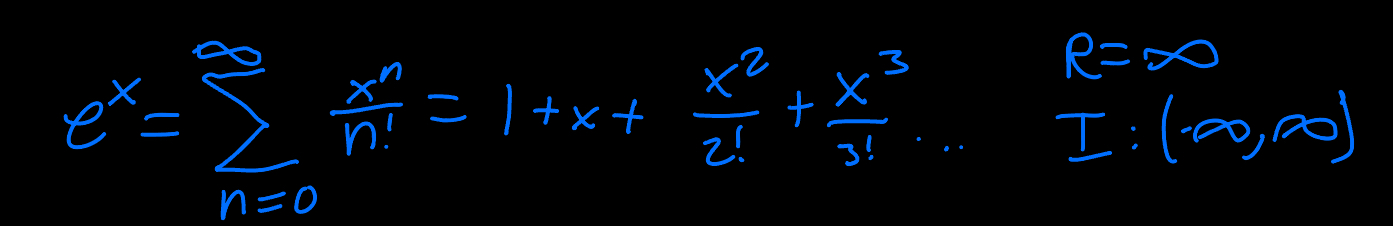
sin(x) Taylor Series

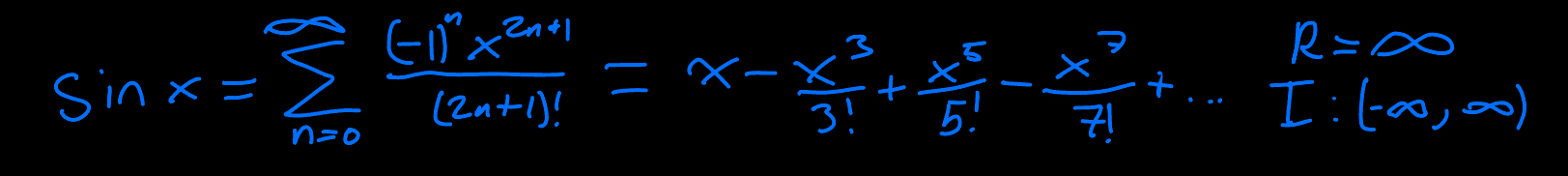
cos(x) Taylor Series

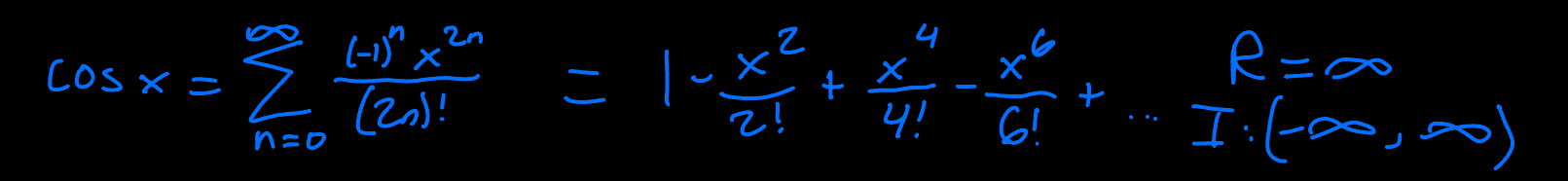
tan^-1(x) Taylor Series

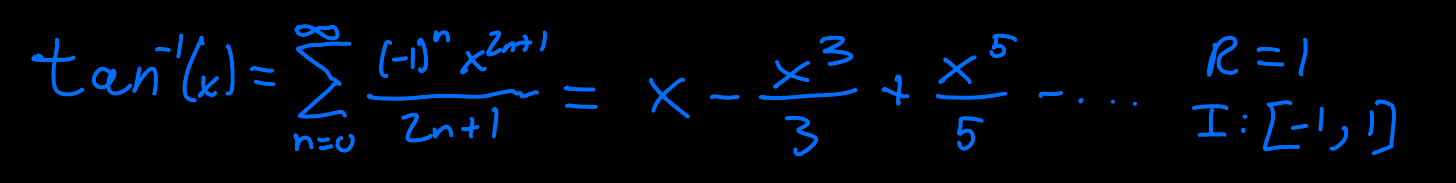
ln(1+x) Taylor Series

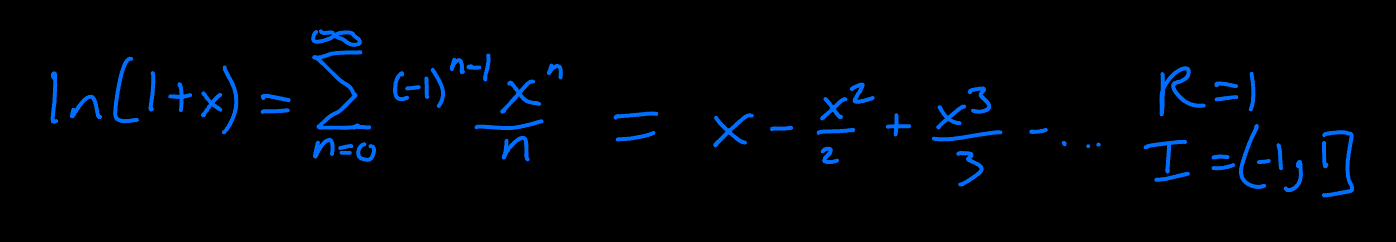
Trig subs

power reduction identity

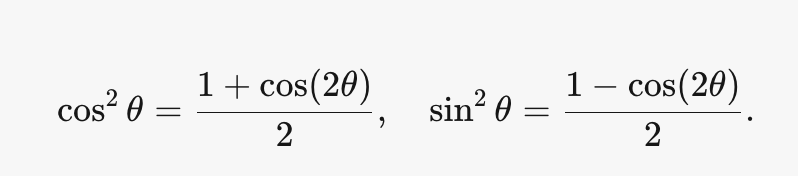
pythagorean identity(sin cos)

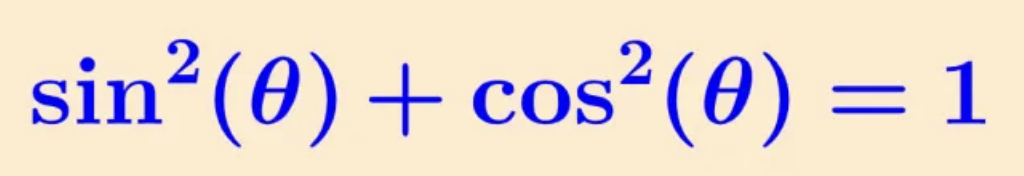
pythagorean identity (tan, sec)

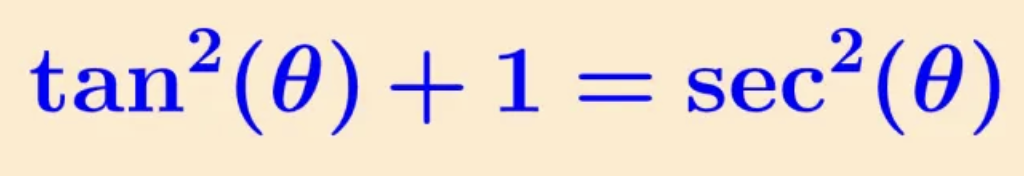
double angle identity

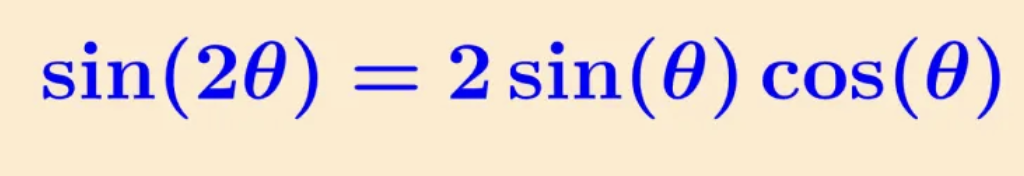
half angle identity