meccanica - TUTTO

cos’è la forza?

È un’interazione che può modificare lo stato di moto o la forma di un corpo.

spiega il primo principio di Newton

Anche detto legge d’inerzia, ci dice che esistono dei sistemi di riferimento INERZIALI per cui un corpo non soggetto a forze permane indefinitivamente nel suo stato di quiete o moto rettilineo uniforme.

spiega il secondo principio di Newton

spiega cosa succede se agiscono delle forze su di un corpo.

L’applicazione di una forza risulta alla variazione del moto del corpo, per cui comporta un’accelerazione o decelerazione.

Al moto però si oppone la massa inerziale, per cui l’accelerazione è direttamente proporzionale alla forza e inversamente proporzionale alla massa inerziale.

F = ma

Spiega in modo DEDUTTIVO il secondo principio di Newton

Posso vedere la relazione F = ma come un’equazione differenziale: F = m d²x/dt²

So che la soluzione di questa equazione è data dalla velocità e dallo spostamento iniziali, e che la forza dipende da spostamento, velocità e tempo. Conoscendo la forza in tutti gli istanti di tempo considerati posso determinare la legge oraria del corpo soggetto a tale forza.

spiega in modo INDUTTIVO la seconda legge di Newton

Conoscendo massa e accelerazione nel tempo, posso indurre la forza che causa tale spostamento. Ciò è stato fatto con le orbite dei pianeti di Keplero, con le quali Newton indusse la legge di gravitazione universale. Oppure con le perturbazioni del moto dei pianeti, che hanno portato Adams e Le Verrier a indurre la presenza di un’altro pianeta, Nettuno.

spiega il terzo principio di newton e un possibile equivoco

Se un corpo esercita una forza (azione) su di un corpo, esso eserciterà una forza uguale e contraria (reazione, 1° proprietà) lungo la stessa retta d’azione (2° proprietà).

Un possibile equivolo sarebbe: ma quindi niente si può muovere!

Prendiamo il caso di un blocco legato ad una fune, che viene tirata fino a far spostare il blocco. la forza esercitata dalla fune ha un punto di applicazione diverso da quella esercitata dal blocco, una si trova sulla fune e l’altra sul blocco. Quindi, considerando solo il blocco per esempio, abbiamo che la forza che agisce su di esso è solo quella della fune, e viceversa.

Cos’è il determinismo Newtoniano?

Il determinismo newtoniano afferma che conoscendo con esattezza lo stato iniziale di un sistema (cioè le posizioni e le velocità di tutte le particelle) e le leggi fisiche che lo governano, è possibile prevedere con certezza tutto ciò che accadrà in futuro, così come risalire a tutto ciò che è accaduto nel passato.

Data un’equazione m d²x/dt² = F, date le condizioni iniziali x₀ e v₀ e nota F nel tempo, esiste una sola funzione x(t) che soddisfa l’equazione.
Quindi il futuro (e il passato) del corpo è completamente determinato.

Dimostrami la conservazione di quantità di moto

Parto da un punto P, a cui viene impressa una forza F. So che

p = mv

derivo

(*) dp/dt = m dv/dt = ma = F (per il secondo principio)

Se ho due corpi che interagiscono, per il 3° principio ho che (£)

F₁₂ = F₂₁

Per (*) F₁₂ = dp₁/dt, mentre F₂₁ = dp₂/dt

Allora, quando vengono sommate, d(p₁ + p₂)/dt = F₁₂ - F₂₁ = 0

Quindi la quantità di moto totale p = p₁ + p₂ è costante e si conserva nel tempo

dimostra la base fenomenologica della 1° proprietà del 3° principio di Newton

Si dimostra tramite la conservazione della quantità di moto durante un urto elastico.

dimostra la conservazione del momento angolare

dL₀ /dt = d(OP x p)/dt = dOP/dt x p + dp/dt x OP = v x p + OP x F

dove

• v x p = 0 perchè v//p

• OP x F = M_o (momento della forza)

Quindi M_o = dL_o/dt

considero L_o = L_o1 + L_o2

derivo:

d(L_o1 + L_o2)/dt = OP₁ x F₁₂ + OP₂ x F₂₁

che per il 3° principio sarebbe

(OP₁ - OP₂) x F₁₂ = P₁P₂ x F₁₂ = 0 perchè parallele

Quindi dL₀ /dt = 0 → L₀ totale si conserva

dimostra che M_o = dL_o/dt

dL₀ /dt = d(OP x p)/dt = dOP/dt x p + dp/dt x OP = v x p + OP x F

dove

• v x p = 0 perchè v//p

• OP x F = M_o (momento della forza)

Quindi M_o = dL_o/dt

cosa dice il teorema di Noether?

Se un sistema ha una simmetria continua che dipende da n parametri, allora esistono n qantità fisiche associate che si conservano.
Con deboli assunzioni Noether trovò che la conservazione della quantità di moto è dovuta all’omogeneità dello spazio, mentre la conservazione del momento angolare è dovuta all’isotropia dello spazio.

differenza tra massa inerziale e massa gravitazionale?

La massa inerziale misura la resistenza di un corpo all’accelerazione quando sottoposto a una forza (F = m_i·a).
La massa gravitazionale misura quanto un corpo subisce o produce forza gravitazionale (F_p = m_g·g o legge di gravitazione universale).
Esperimenti mostrano che sono numericamente uguali (principio di equivalenza), per cui tutti i corpi cadono con la stessa accelerazione in assenza di attrito.

Considerazioni sulla forza peso?

La forza peso è la forza con cui la Terra attrae un corpo di massa m verso il suo centro:

P=mg

È diretta verso il basso (verso il centro della Terra) ed è un caso particolare della forza gravitazionale, valida vicino alla superficie terrestre dove g è quasi costante.

spiegami la reazione vincolare normale

È la forza esercitata da una superficie perpendicolarmente al contatto con un corpo, che impedisce a quest’ultimo di penetrarla. In assenza di altre forze verticali, bilancia il peso (N=P).

spiega la tensione esercitata su un filo

È la forza trasmessa lungo un filo o una corda tesa, diretta sempre verso l’interno del filo (tirando gli estremi). In un filo ideale (massa trascurabile e inestensibile) la tensione è la stessa in ogni punto.

tre leggi di Amontons e Coulomb

• Quando il corpo è fermo:

  Fs < μ_sN

• le superfici iniziano a scorrere se:

  Fs = μ_sN

• se le due superfici scorrono, l’attrito dinamico:

  Fd = μ_dN

0 < μ_d < μ_s < 1

da cosa è originato l’attrito?

Deriva da irregolarità microscopiche delle superfici e da interazioni molecolari tra i punti di contatto. Anche superfici “lisce” presentano asperità che si incastrano e richiedono forza per essere superate.

Più sono i frattali in contatto, più l’attrito sarà forte.

Spiega la formula dell’attrito viscoso

Per velocità piccole, la forza viscosa è proporzionale alla velocità:

Fv = −bv - b’ v |v|

• -bv è il coefficiente viscoso, che dipende dal fluido e dalla forma del corpo. Il segno meno indica che la forza si oppone al moto.

• - b’ v |v| è dovuto alla formazione di vortici

spiega la forza elastica

È la forza con cui un corpo elastico tende a ritornare alla forma iniziale quando viene deformato. Segue la legge di Hooke:

F = −kΔx

dove k è la costante elastica e Δx l’allungamento o la compressione.

cos’è un oscillatore armonico?

È un sistema in cui la forza è proporzionale allo spostamento e diretta verso la posizione di equilibrio:

F=−kx

e segue la legge oraria:

x(t) = A sen (wt + phi)

Esempi: massa su molla, pendolo per piccole oscillazioni. Il moto risultante è armonico semplice, con oscillazioni sinusoidali

Come funziona il pendolo semplice?

È costituito da una massa puntiforme appesa a un filo inestensibile e senza massa, di lunghezza L. Oscilla sotto l’azione della componente tangenziale del peso.

dimostra la formula dell’accelerazione del pendolo semplice

v(t) = v(t) u_T (t)

u_T = (cosa, sina)

calcolo la derivata della velocità

dv/dt = dv/dt u_T + du_T/dt v

du_T/dt = (da/dt -sena, da/dt cosa) = da/dt (-sena, cosa) = da/dt u_N

per il moto circolare v = dx/dt = L da/dt

quindi da/dt = v/L

l’accelerazione è quindi

a = dv/dt = dv/dt u_T + du_T/dt v = dv/dt u_T + v/L u_N v = dv/dt u_T + v²/L u_N

qual è l’equazione per il moto di un pendolo semplice?

equazione di Newton:

• m_i a = T + m_g g

lungo la direzione tangenziale:

• m_i L d²a/dt² = -m_g g sena

lungo la direzione normale:

• m_i L d²a/dt² = T - m^g g cosa

Concentrandomi sull’equazione tangenziale posso effettuare l’approssimazione per piccole oscillazioni, semplificando sina con a:

d²a/dt + m_g/m_i g/L a = 0

che è la classica equazione per l’oscillatore armonico, che ha pulsazione:

w = sqrt(m_g/m_i g/L) = sqrt(g/L)

e periodo:

T = 2pi/w

Cosa s’intende per approssimazione delle piccole oscillazioni?

Quando l’angolo di oscillazione θ è piccolo, si può approssimare sin⁡θ≈θ (in radianti). Questo linearizza l’equazione del moto, che diventa quella di un oscillatore armonico semplice.

dammi la definizione di corpo rigido

Un corpo si dice rigido se la distanza tra qualsiasi sua coppia di punti è fissa. Ciò è dovuto ai legami interatomici che tengono fermi gli atomi.

quanti gradi di libertà ha un corpo rigido?

Fissato un punto A nel corpo rigido, abbiamo 3 coordinate (xyz).

Fissato un secondo punto B esso ha 2 gradi di libertà, perché ha distanza fissa da A.

Fissato un terzo punto C esso ha 1 grado di libertà, perché può solo che ruotare attorno la congiungente A-B.

Quindi in totale un corpo rigido ha 3 + 2 + 1 = 6 gradi di libertà

quali sono i tipi di moto che può compiere un corpo rigido? Dimostra una certa proprietà legata alle velocità

in generale il moto è una successione di coppie rotazione + traslazione infinitesime. In generale l’asse di rotazione cambia nel tempo, infatti viene detto asse di rotazione ISTANTANEO.

Quindi basta conoscere la velocita e la velocità angolare rispetto un asse del corpo per conoscere il suo moto in un istante.

La velocità dipende dalla psizionedella particella del corpo rispetto all’asse di rotazione, ma la velocità angolare no perché descrive l’angolo spazzato in un certo tempo

DIMOSTRAZIONE

Scelgo due punti all’interno del corpo, P e Q, mentre O è il punto per cui passa l’asse di rotazione, allora:

• v_P = v_o + w x OP

• v_Q = v_o + w x OQ

• v_P - v_Q = w x (OP-OQ = w x QP

  quindi v_P = v_Q + w x QP

per cui la velocità angolare è la stessa anche se ho scelto l’asse che passa per Q.

posizione del centro di massa per un corpo rigido?

dato che ρ = dm/dV e che m = ∫dm = ∫ρdV

r_CM = ∫rdm/∫dm = ∫rρdV/ ∫ρdV = 1/m ∫rρdV

se il corpo è OMOGENEO, quindi con ρ costante:

r_CM = ρ/m ∫rdV

quali sono le condizioni necessarie affinché avvenga l’equilibrio?

la somma vettoriale di tutte le forze esterne deve essere nulla, così come la somma di tutti i momenti delle forze esterni

quanti gradi di libertà ci sono nelle rotazioni attorno ad un asse fisso?

quando fisso un punto dell’asse perdo tre gradi di libertà, mentre se ne fisso un’altro (andando quindi a determinare l’asse di rotazione) ne perdo altri 2.

Dai sei gradi di libertà iniziali ne tolgo 5, per cui servirà un’unica equazione per determinare il moto di rotazione attorno ad un asse fisso.

rotazioni intorno ad un asse fisso: determina il momento assiale

uso la seconda equazione cardinale dL_o/dt = M_o

moltiplicandola per il versore u_z ottengo

dL_z/dt = dL_o u_z/dt = M_o u_z = M_z

rotazioni intorno ad un asse fisso: trova la formula che lega L_z a I_z, ovvero il momento angolare al momeno d’inerzia rispetto l’asse z. Cosa succede integrando ancora?rotazioni intorno ad un asse fisso:

So che ogni elemento ruota con velocità v = w x R (w perp. R)

Inoltre il momento angolare di dm è

• dL = r x p = r x dm v = r dm v u_T = r dm w R u_T

u_T = versore perpendicolare a r e v

• dL_z = dL u_z = r dm w R u_T u_z = r dm w R cos(pi/2 - θ) =

  r dm w R sinθ = dm w R²

integro:

• ∫dL_z = L_z = ∫ w R² dm = ∫ w (x² + y²) ρdV = I_z w

integrando ancora:

dL_z/dt = I_z dθ/dt = I_z α = M_z

rotazioni intorno ad un asse fisso: parla del moto del CM

il moto del CM è determinato perché dista R_CM dall’asse di rotazione, per cui:

• a_CM,T = α R_CM

• a_CM,N = w² R_CM

• v_CM = w R_CM

rotazioni intorno ad un asse fisso: ricava l’energia cinetica

K = ∫ ½ dm v² = ∫ ½ ρ v² dV = ∫ ½ ρ w² R² dV = ½ I_z w² = ½ L_z²/I_z

rotazioni intorno ad un asse fisso: teorema delle forze vive e potenza

dW = dK = I_z w dw = I_z dφ/dt dw = I_z dw/dt dφ = M_z dφ

P = dW/dt = M_z w

rotazioni intorno ad un asse fisso: generalizzazione di L_z

Se il moto è completamente determinato dal momento delle forze M_z, lo stesso non vale per il momento angolare L_z. Abbiamo che il momento angolare sia soltanto L_z solo nel momento in cui l’asse di rotazione è l’asse di simmetria.

L = I_z w

momento d’inerzia rispetto un asse di rotazione fisso

I = ∫ R² dm

dove R = distanza punto infinitesimo di massa dm-asse.

= ∫_V ρ R² dV

= ∫_V ρ (x²+y²) dV

momento d’inerzia rispetto all’asse di simmetria di un asta di lunghezza L

I = ∫_-L/2^L/2 x² dm = ∫ ρ x² dx = ρ (L³/24 + L³/24) = m L² / 12

momento d’inerzia rispetto all’asse di simmetria di un anello sottile di raggio R

I = ∫₀^2pi R² dm = ∫ ρ R² dl = ρ R² ∫ dl = ρ R² 2 pi R

circonferenza cerchio

ρ * circonferenza = massa, per cui

I = m R²

oppure

m = ρ * 2 pi R

I = ∫₀^2pi R² dm = ∫ R² R dθ ρ = 2 pi R³ ρ = m R²

momento d’inerzia rispetto all’asse di simmetria di un disco di raggio R

so che ρ = m / pi R²

I = ∫₀^R dr ∫₀^2pi dθ r r² ρ = 2 pi R⁴/4 ρ = ½ m R²

momento d’inerzia rispetto ad un asse di simmetria di un cilindro di raggio R e altezza L

ρ = m / pi R² L

I = ∫₀^R dr ∫₀^2pi dθ r ∫₀^L dz r² s =

= R⁴/4 2 pi L ρ = ½ m R²

momento d’inerzia rispetto ad un asse di simmetria di una sfera di raggio R

ρ = m / 4/3 pi R³

sin²θ = 1 - cos²θ

sinθdθ = -d cosθ

I = ∫₀^R dr ∫₀^pi dθ r sinθ ∫₀^2pi dφ (rsinθ)² ρ =

= 2 pi R⁵/5 ∫_-1¹ d cosθ (1 - cos²θ) ρ =

= 2 pi R⁵/5 (2-2/3) = 2 pi R⁵/5 4/3 m/(4/3 pi R³) = 2/5 R² m

enuncia e dimostra il teorema di Huygens - Steiner

il momento d’inerzia di un corpo rigido rispetto ad un asse che di trova a distanza D dal CM è dato dalla somma del momento di inerzia rispetto ad un asse parallela ma passante per il CM I₀ e del prodotto mD²

I = I₀ + mD²

DIMOSTRAZIONE

nuove coordinate di P:

z’ = z

x’ = x

y’ = y + D

I = ∫_V (x²+y²) dm =

passo alle coordinate del nuovo asse di rotazione

∫ [x’² + (y’ - D)²] dm =

svolgo il quadrato di binomio

∫ [x’² + y’² - 2Dy’ + D²] dm =

= ∫ (x’² + y’²) dm + D² ∫ dm - 2D ∫ y’ dm

• momento d’inerzia rispetto l’asse z’

• mD²

• nullo, perché =my’_CM con y’_CM la coordinata del CM è posta = 0

applicazione di huygens-steiner: calcola il momento d’inerzia di un’asta con punto fisso in uno degli estremi

I = I₀ + mD² = m L² / 12 + m L²/4 = m L² / 3

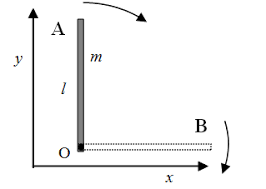
applicazione di huygens-steiner: calcola il momento d’inerzia di un disco con punto fisso in un estremo

I = I₀ + mD² = ½ m R² + mR² = 3/2 m R²

applicazione di huygens-steiner: calcola il momento d’inerzia di una sfera con punto fisso in un estremo

I = I₀ + mD² = 2/5 R² m + m R² = 7/5 R² m

applica il teorema di Huygens-Steiner all’enercia cinetica nel caso di una rotazione attorno ad un asse fisso che non passa per il centro di massa

K = ½ I w² =(H-S)= ½ (I_CM + mD²) w² = ½ I_CM w² + ½ m v²

Va a spiegare il teorema di Konig per l’energia cinetica, infatti

• energia cinetica NEL CM

• energia cinetica DEL CM

quando abbiamo un moto di precessione?

quando c’è un momento esterno non parallelo a L

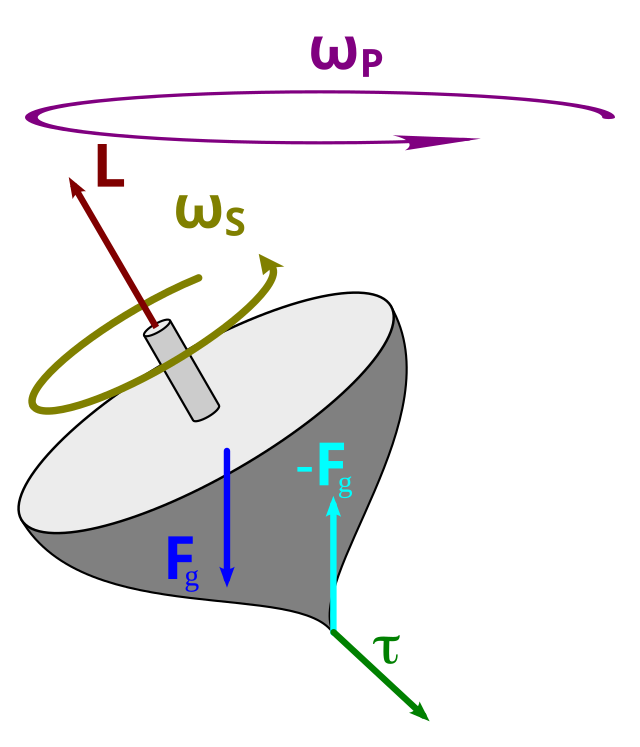
dimostra la velocità angolare di rotazione

considero due masse attaccate da un asta che ruotano sull’asse di rotazione che passa per il centro dell’asta, inclinato di un angolo θ rispetto l’asse.

so che la componente perpendicolare all’asse di rotazione del momento angolare L_p * w = 0

Poiché il moto delle due masse è circolare ci deve essere una forza che le spinge costantemente verso l’interno, ma:

• momento delle forze con forza peso: (r₂ = -r₁)

  r₁ x mg + r₂ x mg = (r₁ - r₁) x mg = 0

allora calcolo per una generica F, sapendo che F₂ = -F₁

• r₁ x F₁ + r₂ x F₂ = r₁ x F₁ + (-r₁) x (-F₁) =

  = 2r₁ x F₁ = M_tot

Che sappiamo essere perpendicolare al piano individuato da r e F (verso individuato dalla regola della mano destra)

Adesso studio il verso z:

dL_z/dt = M_z = 0 perché M è perpendicolare a w

quindi L_z si conserva

L = r₁ x mv₁ + r₂ x mv₂ = 2r₁ x mv₁

quindi L è perpendicolare al piano individuato dai vettori r e v.

F perp v

r x F perp r x v = M perp L = dL/dt perp L

per cui dz/dt = 0 e L * dL/dt = 0

quindi tutto L si conserva → anche L_p

Uso la formula di Poisson per cui esiste Ω perp a L_p e dL_p/dt tale che Ω x L_p = dL_p/dt

Ma L è perpendicolare alla sbarra e ruota con essa, quindi anche L_p ruota con w e pertanto precede

quando avviene un moto di puro rotolamento?

Quando un corpo ruota senza strisciare attorno al punto di contatto

Come si calcola l’energia cinetica di un corpo in moto di puro rotolamento?

K = ½ I_c w² = (H-S) = ½ m v²_CM + ½ I_CM w²

= ½ m (wR)² + ½ I_CM w²

cos’è un urto?

cos’è una forza impulsiva?

cosa succede durante un urto in assenza di forze esterne?

spiega quale energia cinetica può non conservarsi

classifica gli urti

cosa succede durante un urto in presenza di forze impulsive? come ottengo conservazione?

definizione di urto centrale

trova le due velocità finali in un urto elastico centrale

spiega le velocità rispetto al CM

cosa succede se m2 » m1?

se mi sposto nel CM, cosa posso dire sugli urti elastici non centrali?

metodo sperimentale

• esperimento: bisogna raccogliere dati e osservazioni per verificare una teoria e porsi in condizioni le più semplici possibili, eliminando le variabili estranee e controllando le condizioni iniziali (con l’intuito fisico).

• ipotesi: momento di induzione.

• legge fisica: momendo di deduzione. Bisogna dedurre dall’ipotesi la legge che governa ciò che si sta osservando, e trarre varie conseguenze.

• verifica: si compie attraverso vari esperimenti, che possono verificare l’intera legge o restringerne la validità, fino a smentirla del tutto.

leggi fisiche

Relazioni tra equazioni matematiche che servono a descrivere il comportamneto dei fenomeni naturali

equazione dimensionale

Un'espressione matematica che mette in relazione le dimensioni fisiche di una grandezza con altre grandezze fisiche, utile per analizzare e verificare la coerenza di leggi fisiche.

descrivere la posizione di un punto materiale

Retta orientata, sistema di assi cartesiano, levogiro e destrogiro

dimotra che lo spazio è omogeneo

= la scelta di origine è arbitraria…

dimostra che lo spazio è isotropo

= la scelta di direzione (verso degli assi) è arbitraria…

dimostra che il tempo è omogeneo

= la scelta di origine è arbitraria…

il tempo è

omogeneo

lo spazio è

isotropo, omogeneo e pari

regole epistemologiche di Newton

• non ammettere altre cause dei fenomeni oltre a quelle necessarie a spiegarli

• riferire alla stessa causa fenomeni equivalenti

• validità dell’induzione fino a prova contraria (ovvero nuovi fenomeni scoperti che la contraddicono)

dimostra la parità dello spazio

= uguaglianza per simmmetria/riflessione

descrivi le coordinate polari

Sistema di coordinate che utilizza la distanza da un punto fisso e un angolo per determinare la posizione di un punto in un piano.

descrivi le coordinate sferiche

Coordinate utilizzate in un sistema tridimensionale per descrivere la posizione di un punto attraverso un raggio e due angoli.

cos’è una trasformazione di simmetria?

Una trasformazione che mantiene le proprietà geometriche di un oggetto, come la sua forma e dimensione, includendo riflessioni, rotazioni e traslazioni.

dimostra che la traiettoria di un proiettile è una parabola

Si parte dall’equazione del moto lungo l’asse delle x, x(t) = x0 + v₀t.

Se x0 = 0, x(t) = v_0xt

ricavo t = x/v_0x

pongo a sistema le due equazioni del moto sui due assi cartesiani e sostituisco la t nell’equazione delle y: trovo che la traiettoria descritta è quella di una parabola.

dimostra l’angolo che comporta una gittata massima

ISTANTE 0

Si parte dall’equazione del moto lungo l’asse delle x, x(t) = x0 + v₀t.

Se x0 = 0, x(t) = v_0xt

ISTANTE FINALE

ricavo la t dall’equazione sull’asse delle y con la formula risolutiva delle equazioni di secondo grado, con segno positivo. x_finale = v_0xt, per cui sostituisco la t e poi raccolgo v_0y. Se pongo l’altezza h = 0, quindi che il proiettile parte da terra, trovo che x_f = sin2a * v₀²/g
Per cui x_f è massima se 2a = pi/2 → a = pi/4

trova la formula di poisson dalle considerazioni sul moto circolare

Si parte da v = ω x r. Vedo v come dr/dt.

r = R u_r, per cui posso anche scrivere che du_r/dt = ω x u_r.

Generalizzando ad un vettore qualsiasi dA(t)/dt = d/dt (A(t) * u_A) = (derivata di un prodotto)

poi sostituisco du_A/dt con w x u_A, che moltiplicato per A(t) mi da

w_A x A(t).

deduci l’equazione del moto armonico dall’eq. di secondo grado dell’accelerazione e l’equazione del moto circolare.

• a = -ω²x, dove a è l'accelerazione, ω è la pulsazione e x è lo spostamento. Questa equazione descrive il moto di un oscillatore armonico semplice, in cui l'accelerazione è proporzionale e opposta allo spostamento dalla posizione di equilibrio.

  La vedo come un’equazione di secondo grado (d²x/dt² = -ω²x), che risolvo con la formula risolutiva x(t) = c₁sen(ωt + φ) + c2cos(ωt + φ), dove c1 e c2 sono costanti determine dalle condizioni iniziali.

• c1 = v₀/w

• c2 = x₀

  per cui x(t) = v₀/w sen(wt) + x₀ cos(wt)

• x(t) = A sen (wt + phi) = A senwt cos(phi) + A coswt sen(phi)

Quindi, mettendole a confronto, trovo che:

• x₀ = A sen(phi)

• v₀ = wA cos(phi)

• tg(phi) = w x₀ / v₀

• A = sqrt(x₀² + v₀²/w)

• x(t) = Rcoswt = Rsen(wt + pi/2)

• y(t) = Rsenwt

relazione velocità-posizione

inizia da v dv

= v dv/dt dt = a v dt = a dx

poi si integra tra 0 e t, per cui 1/2(v² - v0²) = a (x-x0)

v = sqrt(v0² + 2a(x-x0))

moto con attrito viscoso

a = -kv. Vedo a come dv/dt, poi riordino:

dv/v = -k dt

integro tra 0 e t:

ln v/v₀ = -kt

v/v₀ = e^-kt

v(t) = v₀ e^-kt

mentre x(t) = x₀ + integrale tra 0 e t di v₀ e^-kt dt = x₀ + v₀/k (1 - e^-kt)

per grandi t → x₀ + v₀/k

prodotto scalare

prodotto vettoriale

dammi la definizione di baricentro

il baricentro o centro di massa del sistema è il punto geometrico di coordinate

r_CM = sum(m_i r_i) / sum(m_i)

oppure, con la massa totale M

r_G = 1/M * sum(m_i r_i)

la velocità del baricentro è

v_CM = sum(m_i v_i) / M = p/M

differenziando rispetto al tempo:

dp/dt = M a_G = sum(m_i a_i) = F_i

arriva ad enunciare la prima eq. cardinale della dinamica

la velocità del baricentro è

v_CM = sum(m_i v_i) / M = p/M

differenziando rispetto al tempo:

dp/dt = M a_G = sum(m_i a_i) = F_i (*)

abbiamo ricavato l’equazione m a_i = F_i , ma conviene vedere la forza totale come una somma di forza esterna al sistema F_i^E e una fora interna dovuta alle particelle circostanti F_i^I.

F_i = F_i^I + F_i^E

Per il 3° principio di newton per ogni azione del punto i-esimo sul punto j-esimo F_ji corrisponde una reazione uguale e contraria del punto j-esimo esercitata sul punto i-esimo F_ij = -F_ji

Essendo la somma vettoriale INDIPENDENTE dal punto di applicazione, abbiamo che F_i^I = sum_i=/=j (F_ij) e che quindi

sum_i=1^N(F_i^I) = sum_{i,j = 1}^N(F_ij)

DIMOSTRAZIONE (1 ver)

sum_i<j(F_ij) + sum_j<i(F_ij) =

= sum_i<j(F_ij) - sum_j<i(F_ji)

dato che la somma è indipendente dal nome delle variabili su cui si somma, posso scambiare la i e la j nel secondo termine:

sum_i<j(F_ij) - sum_i<j(F_ij)

DIMOSTRAZIONE (2 ver)

fisso una coppia i, j e considero solo le forze che coinvolgono i e j

F_ij + F_ji = (3° princ) = F_ij - F_ij = 0

quindi (*) sarebbe

dp/dt = sum(m_i a_i) = (2° princ) = sum(F_i^I + F_i^E) = sum F_i^E = F^E

cosa dice il teorema del moto del baricentro? Qual è una sua conseguenza?

il baricentro si muove come un punto materiale in cui sia concentrata tutta la massa del sistema e su cui agisce la risultante delle forze esterne.

La sua conseguenza afferma che per conoscere il moto del baricentro è sufficiente conoscere le forze esterne che agiscono su di esso.

come si effettua il passaggio da un insieme di elementi discreti a un insieme continui di infinite particelle?

basta scomporre il volume in moltissimi volumetti infinitesimi e passare da sommatorie a integrali:

lim_ΔV→0 sum(ΔV_i ρ(r_i) r_i) = 1/M ∫ ρ(r_i) r_i dV

spiega come arrivare alla seconda equazione cardinale della dinamica

Ho un polo O e un vettore r_O che descrive le coordinate di O rispetto l’origine del sistema.

Il momento angolare rispetto ad O è dato da

• L_o = sum L_Oi = sum (OP_i x p_i)

derivo:

• dL_o/dt = sum d/dt(OP_i x p_i) =

  = sum (dOP_i/dt* p_i + OP_i *dp_i/dt) (#)

• d/dt OP_i = v_i - v_o

• (#) diventa sum (v_i - v_o) x p_i + OP_i x F_i

Ma v_i x p_i = 0 perché paralleli, quindi

• -v_o x p_i + OP_i x (sum(F_i^I + F_i^E))

dimostro che posso eliminare le forze interne:

sum_i,j OP_i F_ij = sum_i<j OP_i x F_ij + sum_j<i OP_i x F_ij

adesso cambio i con j e j con i

= sum_i<j OP_i x F_ij + sum_i<j OP_i x F_ij = (1° parte 3° princ)

= sum_i<j (OP_i x F_ij - OP_j x F_ij) = sum_i<j (OP_i - OP_j) x F_ij =

= sum_i<j P_jP_o x F_ij = 0 perché Fij // P_jP_i

Quindi, riprendendeo il discorso di prima

• dL_o/dt = - v_o x p_i + OP_i x (sum(F_i^I + F_i^E)) =

  = - v_o x p_i + sum(OP_i x F_i^E) = -v_o x p + M^E

Questa equazione si semplifica con solo dL_o/dt = M^E se:

• O è fisso (v_o = 0)

• il baricentro è fisso (p = mv_CM = 0)

• v_o // v_CM

• O corrisponde con il centro di massa

spiega la differenza tra ‘nel CM’ e ‘del CM’ e come preferisce distinguerli il prof

una scrittura del tipo v* indica nel CM, ovvero la velocità osservata dal sistema del CM.

una scrittura del tipo v_CM indica la velocità complessiva del CM visto dall’esterno, e viene chiamato del CM

spiega e dimostra il teorema di Konig per il momento angolare

connette il momento angolare rispetto al polo O e quello rispetto al CM. Il teorema ci dice infatti che:

L_o = r_CM x p + (L_CM)*

il momento angolare rispetto un arbitrario polo O = momento angolare del CM + momento angolare del CM.

DIMOSTRAZIONE

so che r_i = r_i* + r_CM e che v_i = v_i* + v_CM

L_o = sum (r_i x m_i v_i) =

= sum ((r_i* + r_CM) x m_i (v_i* + v_CM))

= sum (r_i* x m_i v_i*) + r_CM x sum(m_i v_i*) + sum (m_ir_i*) x v_CM + r_CM x Mv_CM

si eliminano perche p* = 0 e m_ir_i* = 0

• sum (r_i* x m_i v_i*) = L_CM*

• r_CM x Mv_CM = r_CM x p

Ho dimostrato che L_o = L_CM* + r_CM x p

spiega e dimostra il teorema di Konig per l’energia cinetica

l’energia cinetica totale K è la somma dell’energia cinetica DEL CM e dell’energia cinetica NEL CM

K = ½ M v_CM² + K*

DIMOSTRAZIONE

K = sum ( ½ m_i v_i v_i) = sum ( ½ m_i (v_i* + v_CM) (v_i* + v_CM))

= ½ sum (m_i v_i*² ) + ½ v_CM sum(m_i v_i*) + ½ v_CM sum(m_i v_i*) + ½ sum(m_i v_CM * v_CM)

si eliminano perché p* = 0

• ½ sum (m_i v_i*² ) = K*

• ½ sum(m_i v_CM * v_CM) = ½ M v²_CM

parla delle coniche e come trovare l’equazione del raggio in funzione dell’eccentricità e di un certo parametro p

differenzia i tre casi: e<1, e=1 e>1 e spiega il perché

differenza tra epicIclo e deferente

Che cos’è il deferente nel modello tolemaico?

È la grande circonferenza lungo la quale si muove il centro dell’epiciclo. Rappresenta il percorso principale del pianeta attorno alla Terra (posta vicina al centro, o in un punto leggermente decentrato detto eccentrico).

Che cos’è l’epiciclo?
È la piccola circonferenza sulla quale si muove il pianeta, il cui centro a sua volta percorre il deferente. Serve a spiegare i moti retrogradi osservati nei pianeti.

arriva alla formulazione della prima legge di Keplero

spiega la seconda legge di keplero

parla della terza legge di keplero