Discrete maths 1 - propositional logic

Define proposition

A statement that is either true or false

Define a law (for propositional calculus)

a fact about a proposition that holds regardless of the truth values of the proposition

Define a tautology (informally)

A proposition that is always true, regardless of “what the world looks like” (what the truth values of the variables contained are)

define a tautology (formally)

A Boolean formula F with variables X1,...,Xn where the value of F is t for any assignment of true/false values to the variables Xi.

define indentically false (informally)

A proposition that is always false, regardless of “what the world looks like” (what the truth values of the variables contained are)

define indentically false (formally without tautology)

A Boolean formula F with variables X1,...,Xn where the value of F is f for any assignment of true/false values to the variables Xi

define indentically false (formally by tautology)

A Boolean formula F with variables X1,...,Xn where ¬F is a tautology

what is the smallest possible proposition (an “atomic” proposition)

a single variable that is either true or false (e.g. X)

What are connectives (for propositional calculus)

Symbols for combining (or modifying) propositions to form new propositions

Define x∧y

x∧y is true if both x and y are; it is false otherwise.

define x∨y

x∨y is true if either x or y is true, or if both are true; it is false otherwise.

define ¬x

¬x is true if x is false, it is false otherwise.

define x → y

x → y is false if x is true and y is false, it is true otherwise. 

in the proposition x →y, what is x called?

the antecedent

in the proposition x →y, what is y called?

the consequent

Given a collection of variables, X1...Xn, define boolean formulae (formally)

a string of symbols from the set {X1, … , Xn, ∧,∨,¬,→,(,) }

where any variable Xi is a boolean formula, and if F and G are Boolean formulae, so are (F ∧ G), (F ∨G), (F → G) and ¬F

define boolean formulae using BNF

F ::= X | (F ∧F) | (F ∨F) | (F →F) | ¬ F

(“the formula F is either a variable, the conjunction of two formulae, the disjunction of two formulae, the implication of two formulae, or the negation of a formula”)

What does it mean to “evaluate” a boolean formula (informally)?

assign truth values to each variable of the formula, then use the definitions of the connectives to find the truth value of the formula itself.

define valuation/truth assignment (formally)

A valuation v over Boolean variables X1 ...Xn is a function associating to each variable Xi a truth value v(Xi), either t or f.

How is the definition of a valuation written?

big curly bracket with conditions for the outcomes t and f, as in img.

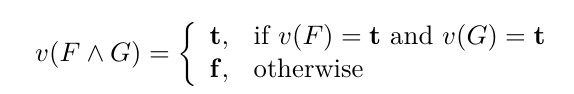
What is an inductive definition?

one that defines the value of the function on complex formulae in terms of its value on subformulae

define logical equivalence (between two statements)

A pair of formulae F1 and F2 are logically equivalent if F1 implies F2 AND F2 implies F1 i.e. F1 is true if and only if f2 is true

Written (F1 → F2)∧(F2 →F1) or F1 ≡ F2

define logical equivalence mathematically

F1 ≡ F2 if and only if v(F1) = v(F2) for every valuation v

What are the three basic laws of ∧ and ∨?

Commutativity

Associativity

Distributivty

state the commutative law

given variables X, Y, X∧Y ≡ Y∧X and X∨Y ≡ Y∨X

i.e. the arrangement of variables around a commutatve operator does not affect its valuation.

what type of boolean formula are all of the basic operator laws for con/disjunction

tautologies

What does the statement “logical equivalence is a congruence” mean?

If two formuale are equivalent, then their logical implications are also equivalent i.e. a formula can be replaced by its logical equivalent in any larger formula, and this will not affect the value of the formula for any inputs. 

state the associative law

For variables X, Y and Z, X∨(Y ∨Z) ≡ (X∨Y)∨Z

i.e. order of operation will not affect valuation of a formula

define the distributive law(s)

X∧(Y ∨Z)≡(X∧Y)∨(X∧Z) (disjunction over conjunction)

X∨(Y ∧Z)≡(X∨Y)∧(X∨Z) (conjunction over disjunction)

i.e. you can “split” an operator acting on a formula to multiple formulae that give the same outcome when connected

State De Morgan’s Law(s)

Given variables X and Y,

¬(X ∧Y) ≡ (¬X∨¬Y)

¬(X ∨Y) ≡ (¬X∧¬Y)

State the law of excluded middle

X ∨¬X

state the law of double negation

¬¬X ≡ X

State the law of proof by contradiction (reductio ad absurdum)

((¬X → Y)∧(¬X →¬Y)) → X

state the law of implication (the CNF of implication)

(X →Y) ≡ (¬X∨Y)

State the modus ponens law (law for going from x and x → y to y)

(X ∧(X →Y)) → Y

What does “reducing the problem of proving y to proving x” mean?

A method for proving a proposition y where we prove that x implies y, and then prove x to conclude y.

What is special about the NAND operator?

Any boolean formula can be written in terms of only NAND

Why is CNF important?

Makes designing circuits from logic easier

Define the Disjunctive Normal Form formally

F1 ∨F2 ∨···∨Fn

where each Fi is of the form L1 ∧L2 ∧···∧Lki

and each Li is either a variable, X, or the negation of a variable, ¬X

Define the Disjunctive Normal Form using BNF

L ::= X|¬X

C ::= L|(L∧C)

D ::= C|(C∨D)

What is the DNF theorem?

Every boolean formula is equivalent to one in DNF

What is the standard method for generatinjg DNFs using truth tables

Look at the truth table and define each possible combination of outcomes separately

e.g. if the formula is true when X = t, Y = t, Z = t

then it is true when X /\ Y /\ NOT Z

combining each “combination” using \/ will yield a DNF formula

What is the method for generating DNFs using laws

Get rid of all the → connectives using the law X → Y ≡ ¬X ∨Y

Push all the negations in as far as possible using the De Morgan laws and the law ¬¬X ≡ X.

Push all the conjunctions in as far as possible using distributive laws.

Define conjunctive normal form mathemativally

F1 ∧F2 ∧···∧Fn

where each Fi is of the form L1 ∨L2 ∨···∨Lki

and each Li is either a variable, X, or the negation of a variable, ¬X

What is the CNF theorem?

Every Boolean formula is equivalent to one in CNF

How could the CNF theorem be proved using the DNF theorem?

Using the DNF equivalent of a formula F, use De Morgan’s law to convert DNF to CNF