РТ-2 Линал

Определение линейного оператора

Эндоморфизм

Если X=Y

Изоморфизм

Если существует обратный оператор, который тоже является линейным(?)

Автоморфизм

Если эндоморфизм и изоморфизм

Ядро линейного оператора

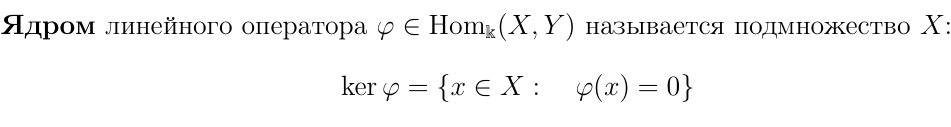
Образ линейного отображения

Чем еще является ядро?

Линейным подпространством X(k)

Чем еще является отображение?

Линейным подпространством Y(k)

Теорема об изоморфизме

Определение ЛНЗ набора

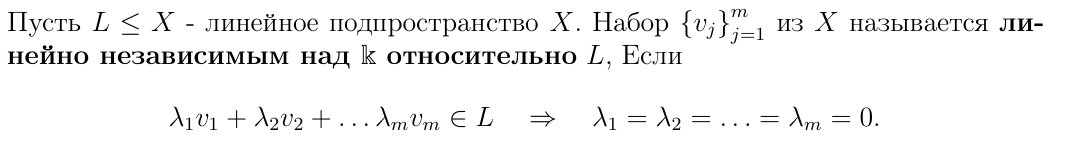
Говорят, что набор порождает X относительно L, если

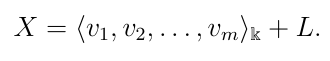
Определение базиса X относительно L

Лемма о базисе (3 эквивалентных утверждения)

Лемма-следствие о размерностях

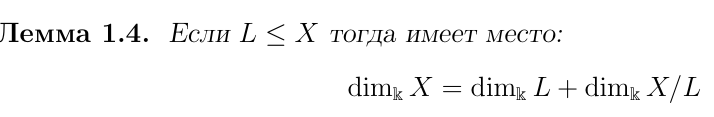
Теорема о ядре и образе (о ранге и дефекте)

Операторы равны, если

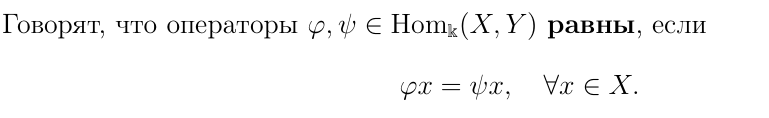
Определение суммы линейных операторов

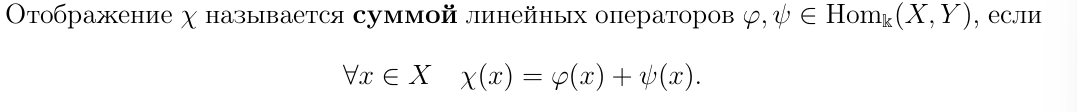
Является ли сумма линейных операторов линейной?

Есс

Определение умножения линейного оператора на число

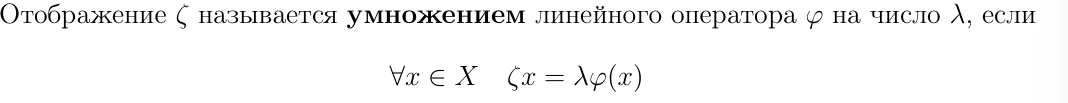
Является ли такое отображение(умножение оператора на число) линейным?

Да

Является ли множество линейных операторов линейным пространством?

Да. Множество Hom_k(X,Y)- линейное пространство над полем k.

Определение матрицы линейного оператора

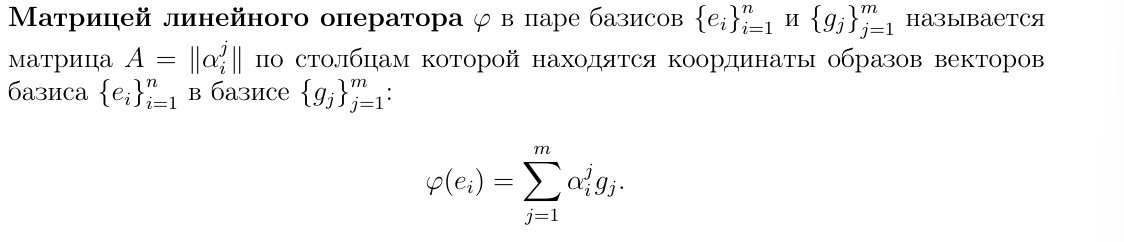
Теорема о связи линейного оператора и матрицы

Задание линейного оператора φ эквивалентно заданию его матрицы A в фиксированной паре базисов.

4 следствия из эквивалентности задания линейного оператора и его матрицы

1. Hom(X,Y) ≃ M_mxn

2. End(X) ≃ M_n (алгебра квадратных n×n матриц)

3. ψ◦φ↔B_ψ·A_φ

   λφ↔λA_φ
   φ+ψ↔A_φ+B_ψ

4. dimHom(X, Y) = dimX · dimY

   dimEnd(X) = (dimX)²

Определение базиса пространства Hom_k(X,Y)

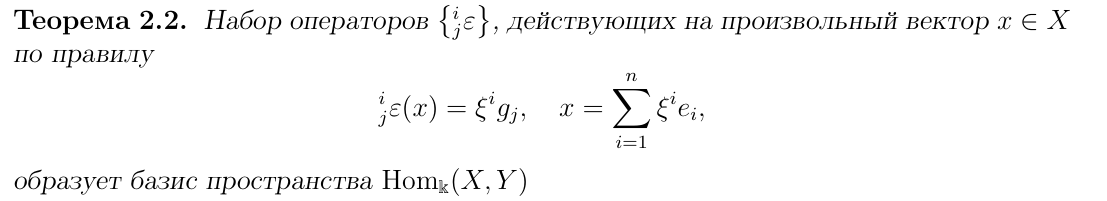
Теорема о смене базиса

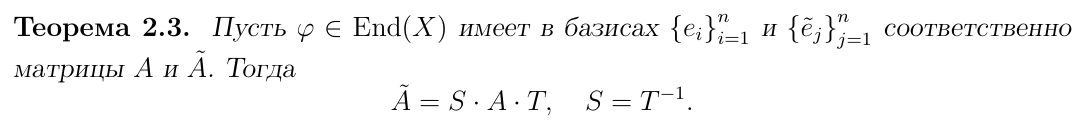
Преобразование матрицы произвольного оператора φ∈Hom_k(X,Y) с матрицами перехода T_X и T_Y имеет вид:

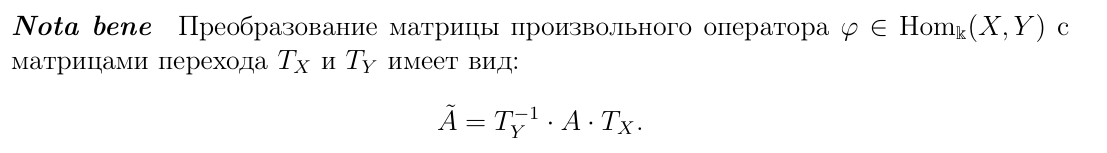
Определение композиции линейных операторов

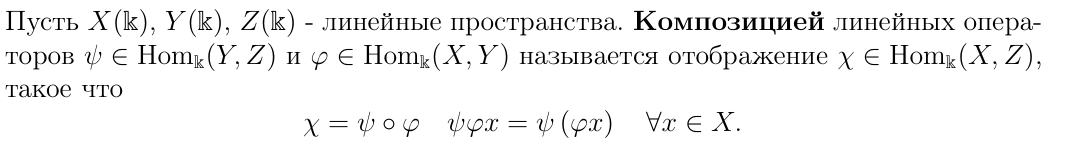
Является ли отображение композиции линейных операторов линейным оператором?

Ес оф корс

Определение алгебры

Алгеброй называется кольцо, снабженное структурой линейного пространства

Определение структурных констант алгебры

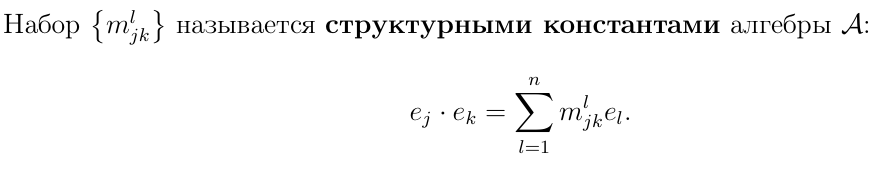
Какую алгебру мы называем алгеброй операторов над пространством X(k)

Алгебру End_k(X)

Определение обратимого оператора

Оператор φ, для которого существует φ˜ , обладающий следующими свойствами, называется обратимым

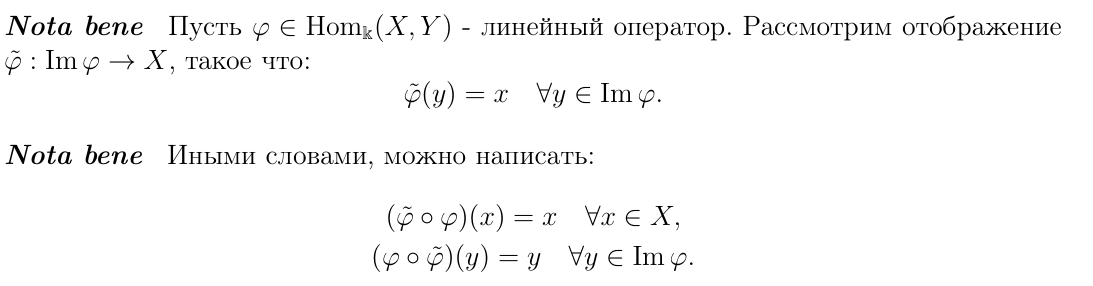
Определение обратного оператора

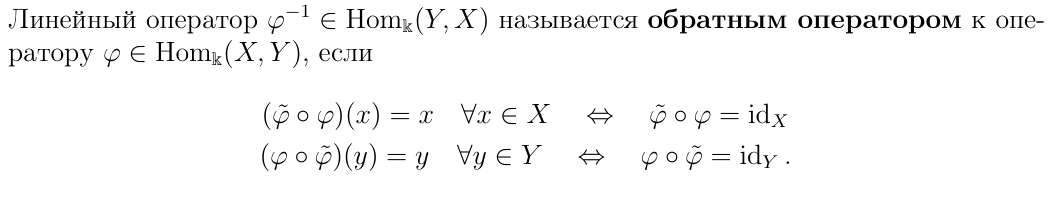
Теорема о существовании обратного оператора

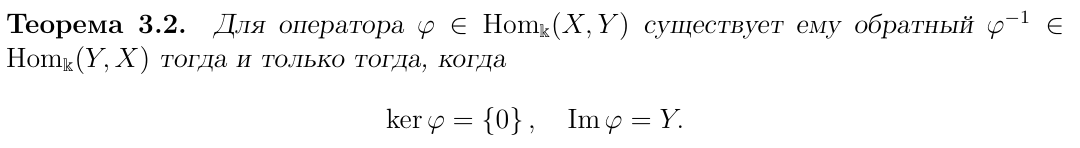
Необходимое условие существования обратного оператора

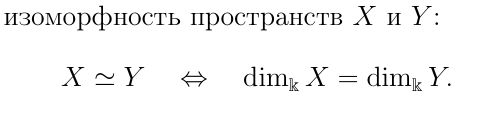
Свойства отображения φ → φ⁻¹

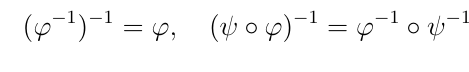
Определение тензорного произведения операторов

Является ли отображение тензорного произведения операторов линейным оператором? (ответ убил..)

да.

Определение тензорной степени оператора

Определение внешней степени пространства

Определение определителя набора векторов

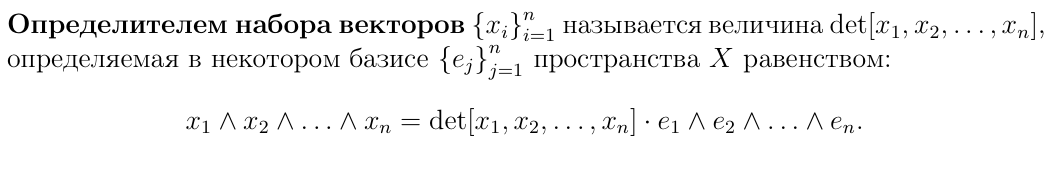
Определение внешней степени оператора

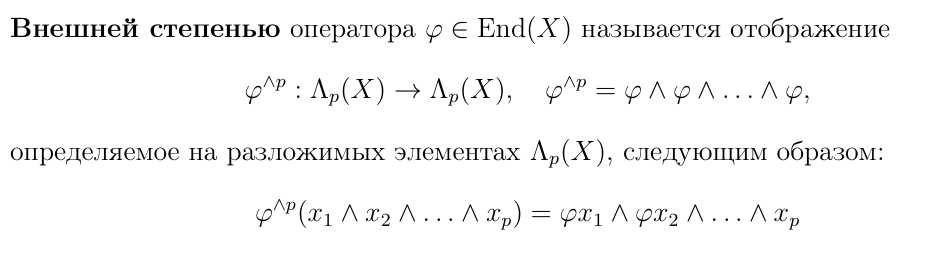
Определителем линейного оператора φ называется величина det(φ), которая определяется…

следующим равенством:

φ^∧n(e₁ ∧ e₂ ∧... ∧e_n) = det(φ) · e₁ ∧e₂ ∧...∧e_n

С чем совпадает определитель линейного оператора в заданном базисе?

С определителем его матрицы в этом базисе

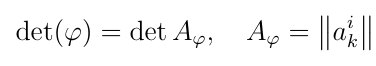
Зависит ли определитель линейного оператора от базиса?

Нет

Для любого z ∈ Λ_n(X) имеет место …

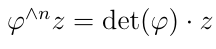
Определение унитальной алгебры

Алгебра A называется унитальной, если в ней существует элемент 1_A ∈ A, называемый единицей алгебры, такой что:
x · 1_A = x=1_A·x ∀x∈A

Определение инвариантного подпространства

Пусть φ ∈ End_k(X) - эндоморфизм линейного пространства X(k). Подпространство L(k) ≤ X(k) линейного пространства X(k) называется инвариантным подпространством линейного оператора φ, если ∀x ∈ L:

φx∈L ⇔ φ(L)⊂L

Определение ультраинвариантного подпространства

Инвариантное подпространство L линейного оператора φ называется ультраинвариантным подпространством, если существует его дополнение L′, которое тоже является инвариантным подпространством

Является ли дополнение ультраинвариантного подпространства ультраинвариантным?

Да, следует из определения

Определение компоненты оператора φ в ультраинвариантном подпространстве L

Оператор φ_L называется компонентой оператора φ в ультраинвариантном под пространстве L, если φ_L ∈ End_k(L) и φL(x) = φ(x) ∀x ∈ L

Лемма о прямой сумме ульраинвариантных подпространств оператора φ

Определение идеала алгебры скалярных полиномов

Идеалом алгебры k[t] называется такое ее линейное подпространство, что k[t] · I ⊂ I

Лемма об идеале

Пусть q ∈ k[t], тогда множество q ·k[t] является идеалом

Определения главного идеала и порождающего полинома идеала

Идеалы вида q · k[t], q ∈ k[t], называются главными идеалами кольца k[t], а полином q называется порождающим полиномом идеала

Любой идеал в кольце k[t] является….

главным

Определение минимального полинома идеала

Минимальным полиномом идеала а называется нетривиальный полином p_a наименьшей степени, принадлежащий идеалу a.

Лемма о делимости и минимальном полиноме

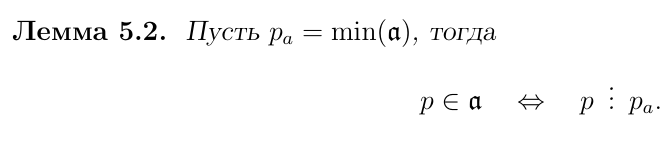
Определение суммы двух идеалов

Суммой a₁ + a₂ двух идеалов a₁ и a₂ называется множество
b = {p∈k[ t ] | p=p₁+p₂, p₁ ∈a₁, p₂ ∈ a₂}

Чем является множество b = {p∈k[ t ] | p=p₁+p₂, p₁ ∈a₁, p₂ ∈ a₂}

Идеалом

(идеалы) a₁ ⊂ a₂ тогда и только тогда, когда..

p1 делится на p2

Пусть a₁ - главный идеал с порождающим полиномом p₁ и a₂ - главный идеал с порождающим полиномом p₂, тогда…

1. a₁ ∩ a₂ = (p), p = ⟨p₁, p₂⟩

2. a₁ + a₂ = (p), p = (p₁, p₂)

Пусть p₁, p₂ такие что (p₁, p₂) = 1, тогда…

∃q₁, q₂ ∈ k[t] : p₁q₁ +p₂q₂ = 1

Пусть p = p₁, p₂,...,p_k, где (p_i,p_j≠i) = 1 тогда…

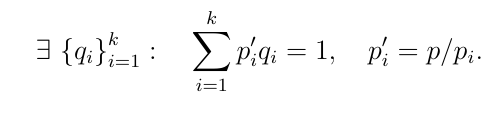
Определение операторного полинома

Определение аннулирующего полинома

Всякий полином из ker σ_φ называется аннулирующим полиномом оператора φ

Тривиален ли идеал ker σ_φ ?

Нет

Определение минимального аннулирующего полинома линейного оператора

Минимальным аннулирующим полиномом линейного оператора φ называется минимальный порождающий полином идеала ker σ_φ

Лемма об изоморфизме для фактор-структур иделов

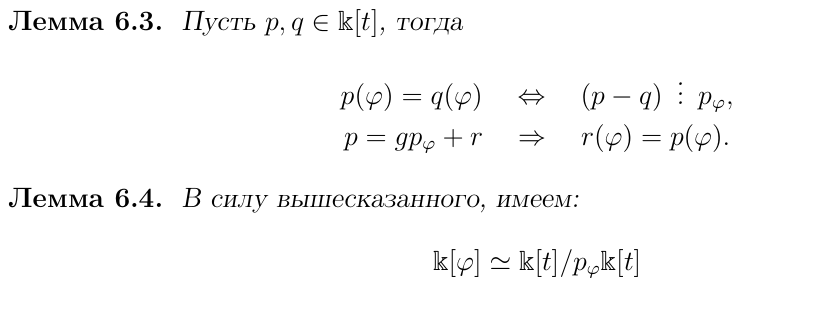
Лемма о разложении операторной единицы

Лемма о прямой сумме и ядрах:

Пусть p_φ(t) = p₁(t)·p₂(t), причем (p₁,p₂) = 1, тогда…

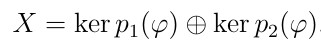
Лемма о ядрах и отображениях:

Пусть p_φ(t) = p₁(t)·p₂(t), причем (p₁,p₂) = 1, тогда…

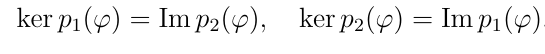
Лемма о изоморфности фактор-структур ядра:

Пусть p_φ(t) = p₁(t)·p₂(t), причем (p₁,p₂) = 1, тогда…

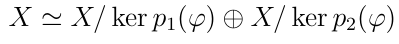
Пусть p_φ(t) = p₁(t)·p₂(t), причем (p₁,p₂) = 1, тогда проекторы на соответствующие подпространства kerp1(φ) и kerp2(φ) имеют вид…

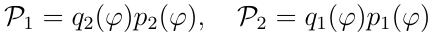
Структурная теорема

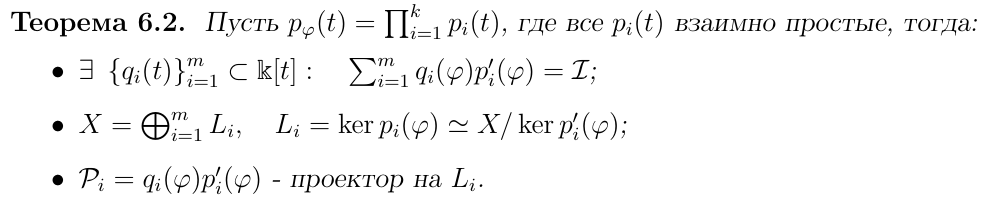
Определение характеристического полинома линейного оператора

Зависит ли характеристический полином от выбора базиса?

Нет. Характеристический полином χ_φ(λ) является функцией от λ, не зависящей от базиса

Теорема Гамильтона-Кэли

Характеристический полином линейного оператора φ является его аннулирующим полиномом:

χ_φ ∈ (p_φ)

Определение инварианта линейного оператора

Инвариантом линейного оператора называется такая его числовая функция, значение которой не зависит от выбора базиса

Определение собственного вектора

Собственным вектором оператора φ называется вектор x ∈ X, такой что

x≠0, φx=λx, λ∈k,

при этом λ называется собственным числом линейного оператора φ

Определение спектра

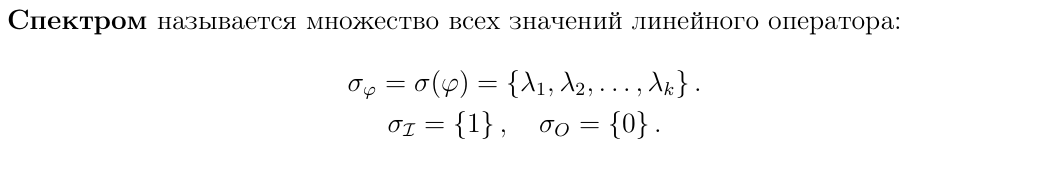
Собственные векторы, отвечающие различным собственным значениям являются ЛЗ/ЛНЗ (выбрать нужное)

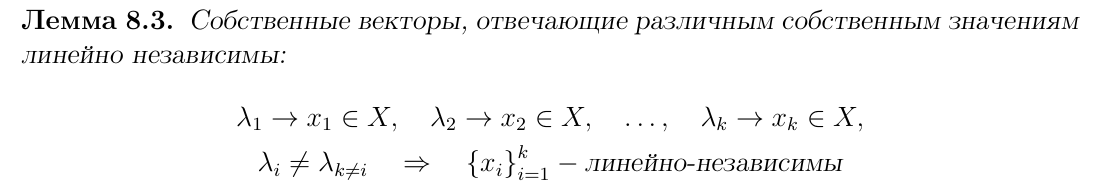
Определение характеристического числа линейного оператора

Корень характеристического многочлена называется характеристическим числом линейного оператора

Определение оператора скалярного типа

В каком случае собственное значение является простым?

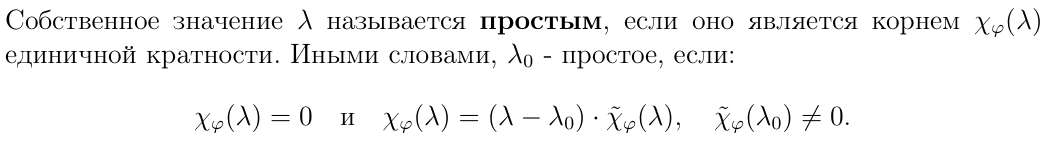
Если у оператора все собственные значения являются простыми, то он называется оператором с..

С простым спектром

Спектральная теорема 2.0

Теорема-определение геометрической кратности

Пусть φ∈End_k(X) - линейный оператор и L_r=kerφ^r, тогда имеет место последовательность….

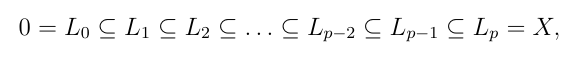
Пусть τ∈End_k(X) - нильпотентный оператор порядка p, то есть τ^p=0, тогда каждое включение в последовательности - (какое?)

точное

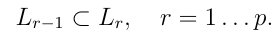
Определение базиса Жордана

Лемма-условие на блочно-диагональный вид жорданова базиса

Определение Жордановой нормальной формы

Определения алгебраической, полной и геометрической кратностей

Лемма о связи алгебраической, спектральной и полной кратностей

Алгебраическая и спектральная (геометрическая) кратности не превосходят полной:

1 ≤ m_i ≤ n_i, 1 ≤ r_i ≤ m_i