Algebra 1 EOC Review

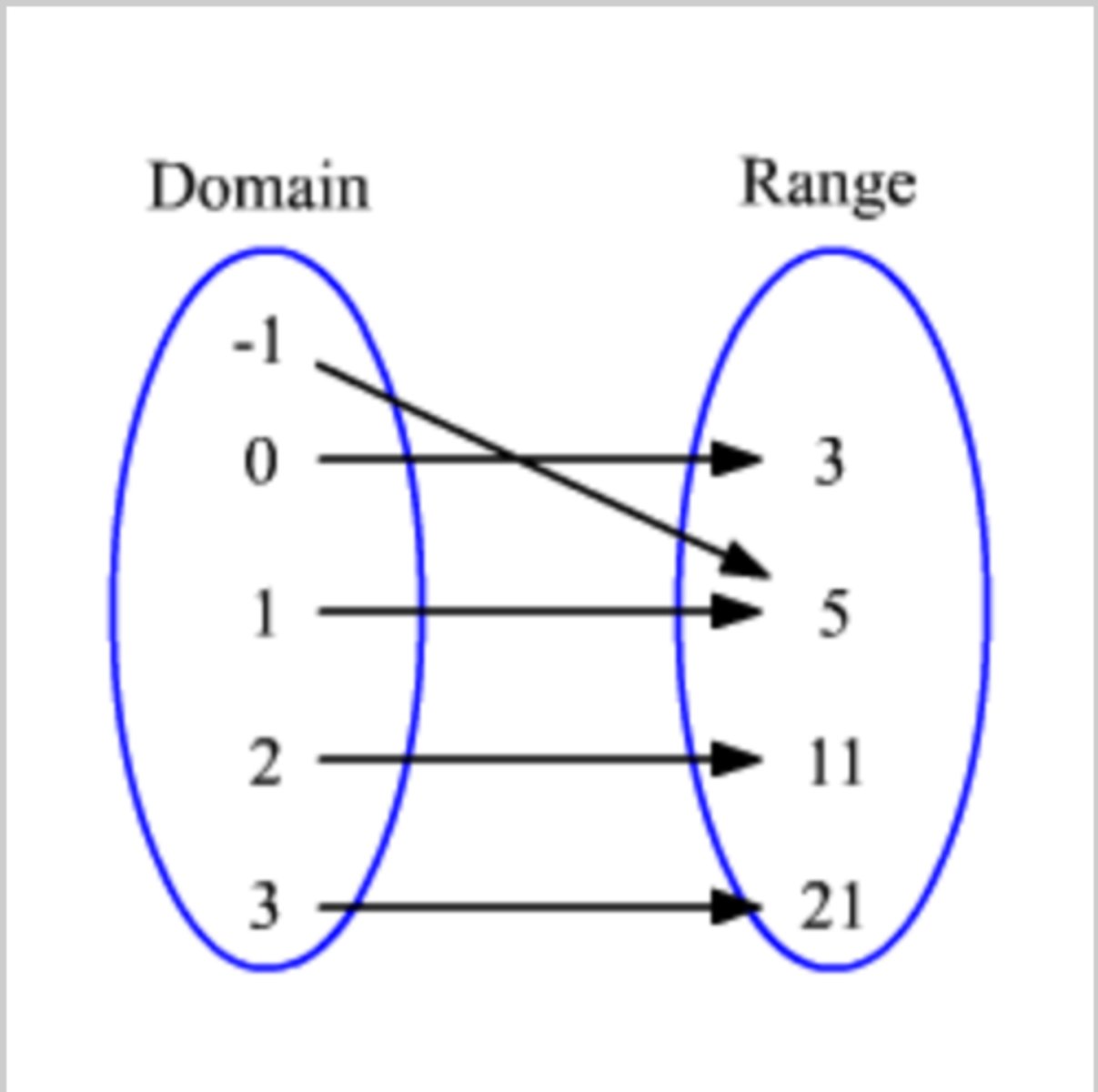
relation

set of ordered pairs

ordered pair

the x and y coordinates of a point on the coordinate plane (x,y)

coordinate plane

a plane formed by 2 perpendicular lines called axes (the x-axis goes sided to side, the y-axis goes up and down).

function

special relation where each x-value is paired with ONLY ONE y-value. (x-values DO NOT repeat, it passes the vertical line test)

Mapping

Bubbles that represent the x-values and the y-values.

Table

A way to represent ordered pairs.

domain

set of all of the possible x-values. INPUTS

range

set of all the possible y-values. OUTPUTS

variable

NOT A NUMBER. A letter or symbol that stands for a number.

independent variable

the INPUT or CAUSE in a situation or problem. It's the variable YOU CAN control. It's the X variable.

dependent variable

the OUTPUT or RESULT in a situation or problem. It's the variable YOU CANNOT control. It's the Y variable. In a equation, its the variable BY ITSELF on one side of the = sign.

other names for "x"

domain, independent variable, input

other names for "y"

range, dependent variable, output

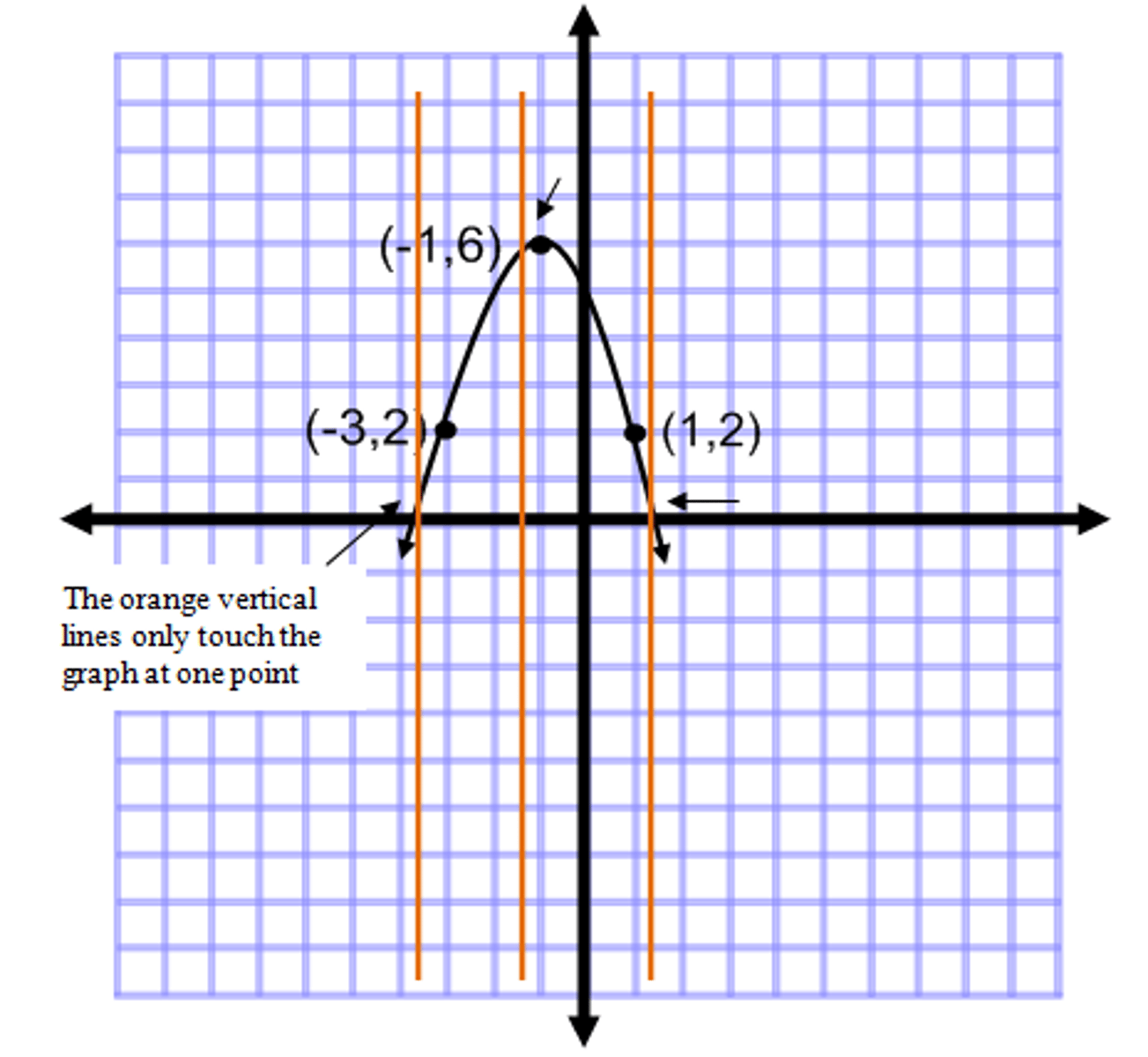
vertical line test

a relation is a function and passes the vertical line test if when a vertical line is drawn through the graph, it touches the graph only ONE time.

discreet function (scatter plot)

data appears as individual points on a graph. Whatever is being graphed cannot be broken down in to smaller pieces.

continuous function

data appears as a smooth curve on a graph.

graph of a linear function

Linear Function Parent Graph

graph of a quadratic function

Quadratic Parent Function

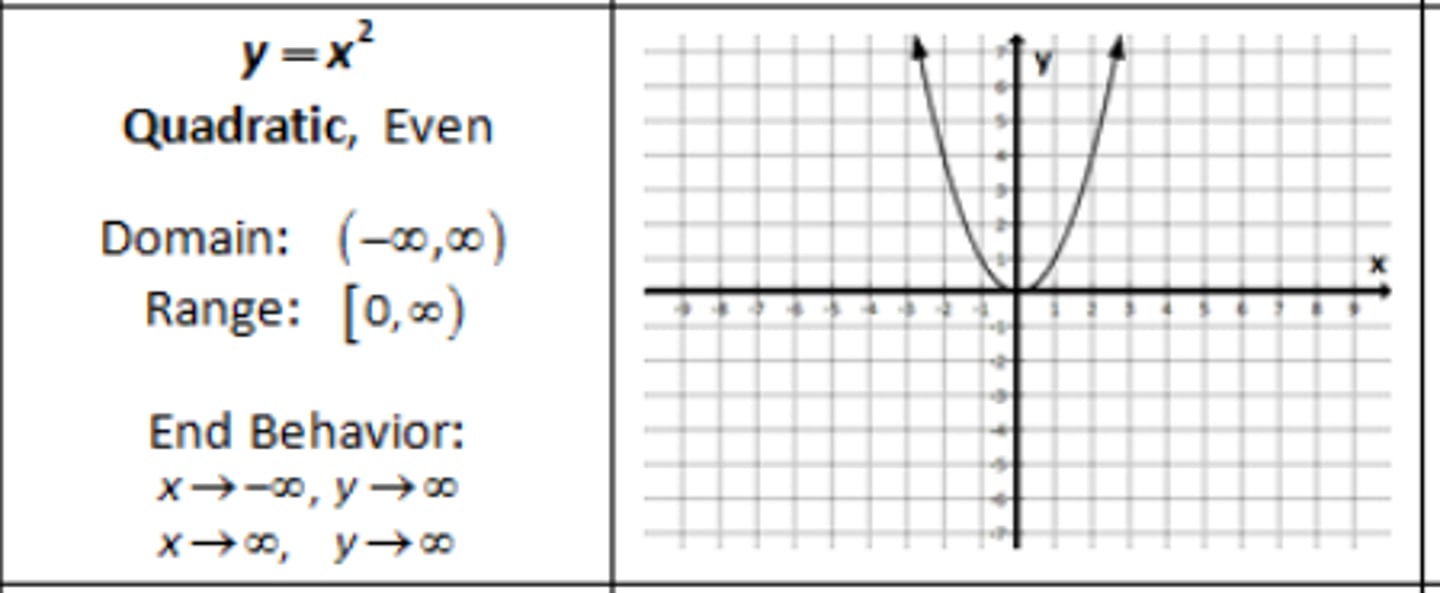
graph of an inverse function: y=1/x

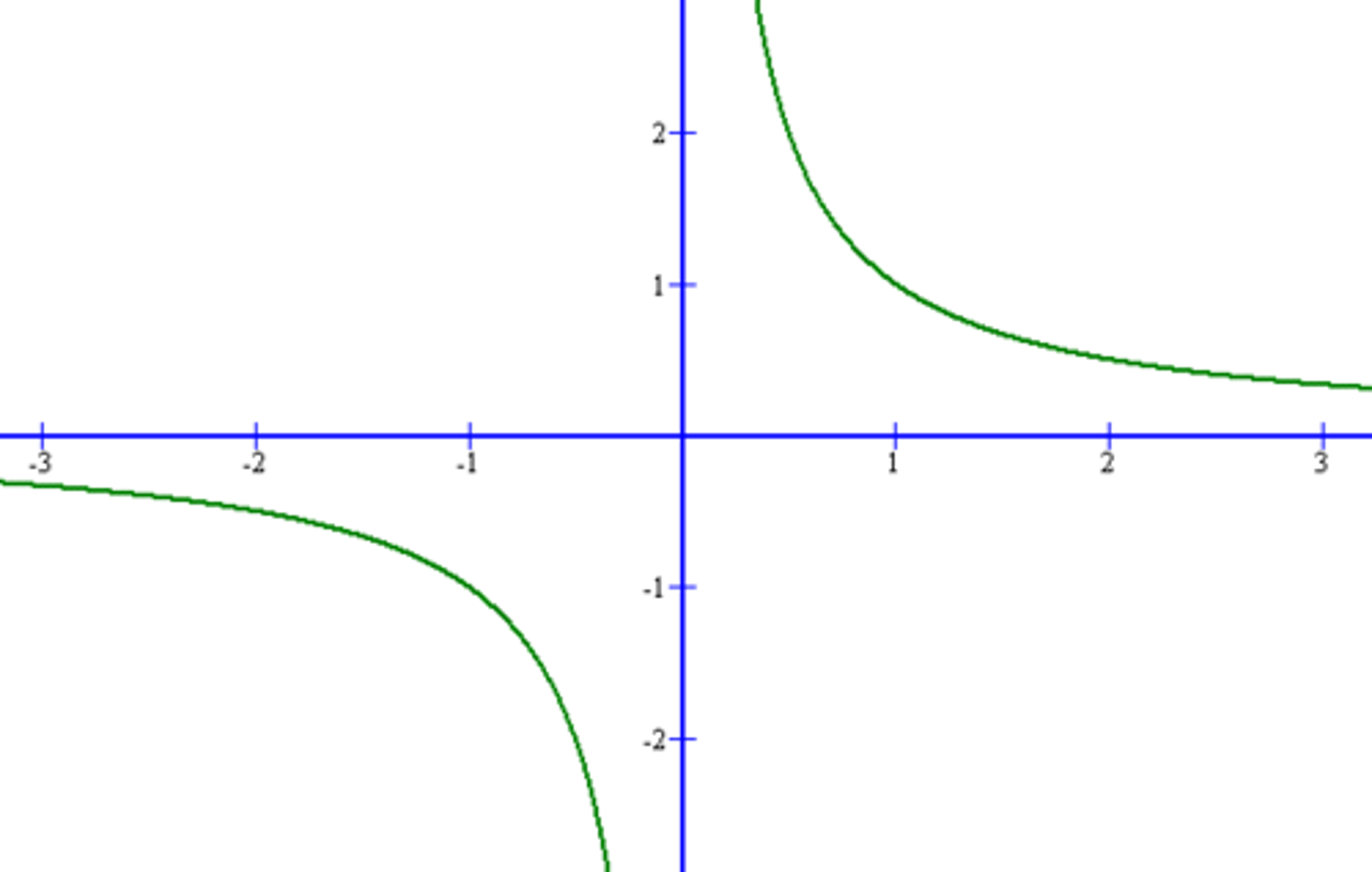
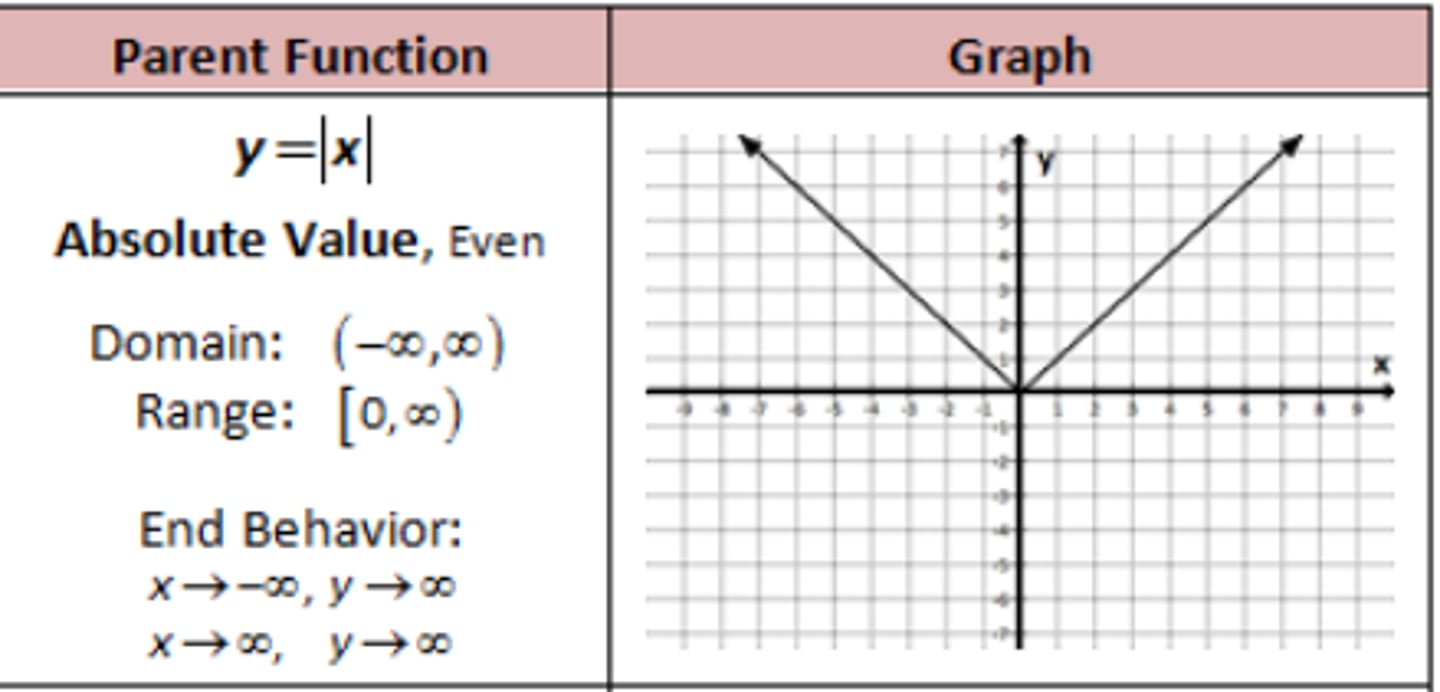
Absolute Value Parent Function

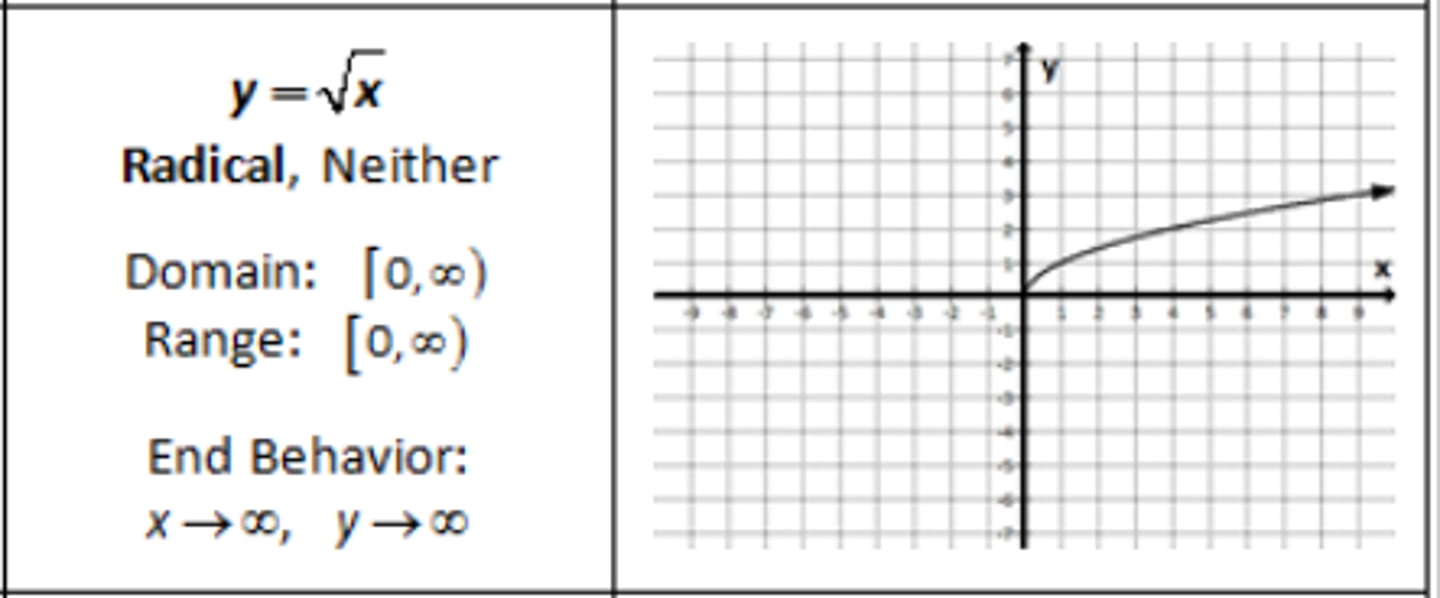
Radical (square root) Parent Function

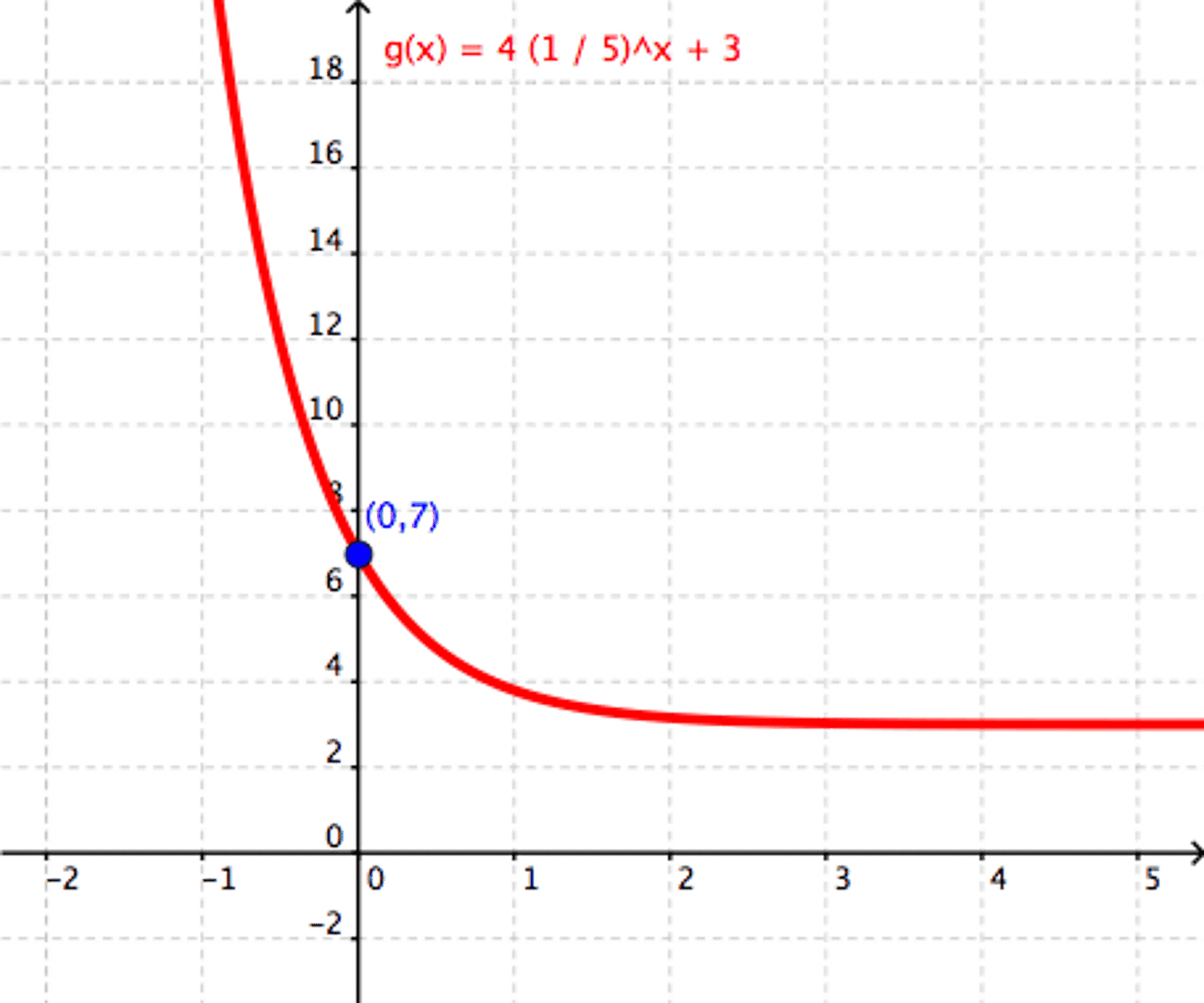
graph of exponential decay function

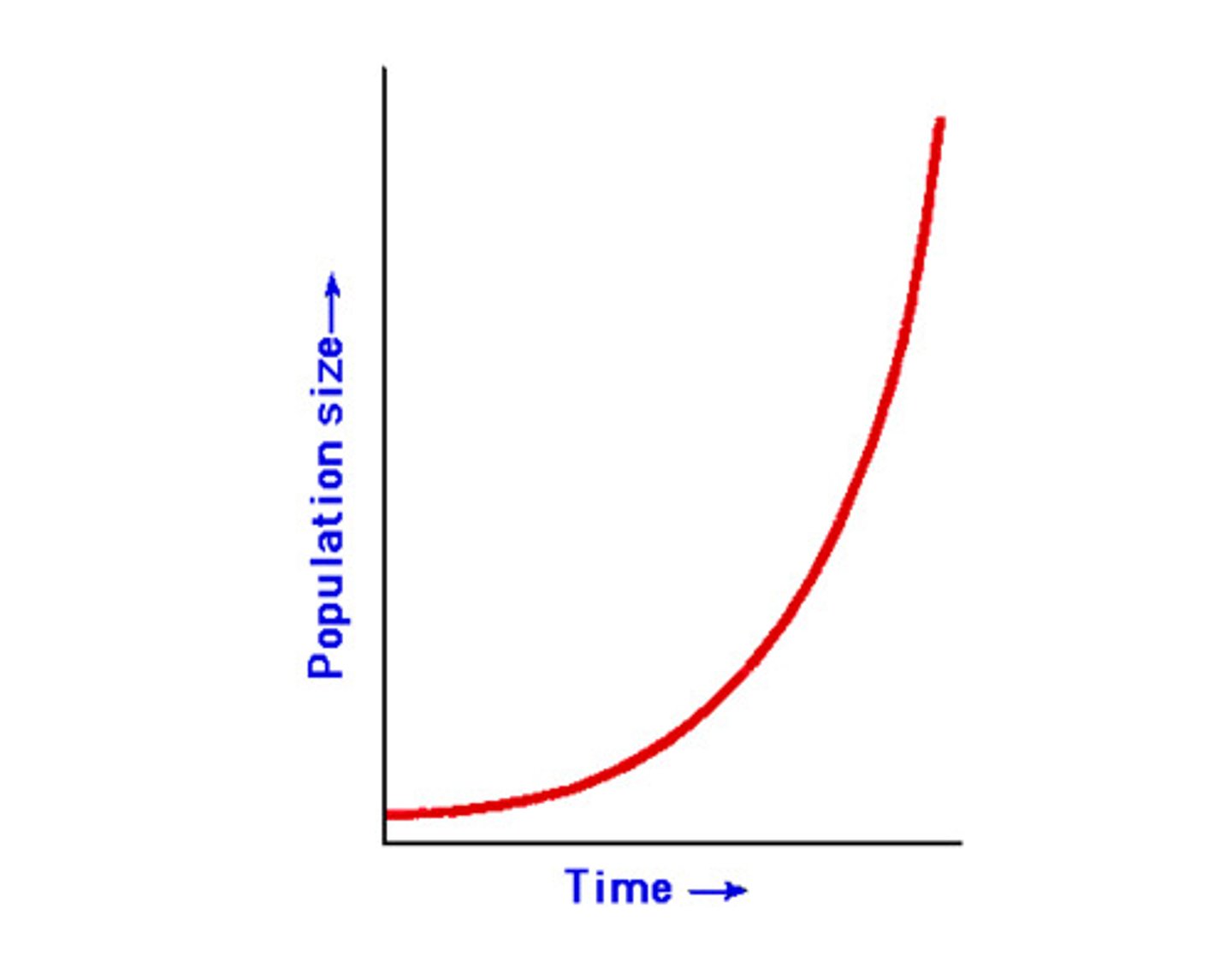
graph of exponential growth function

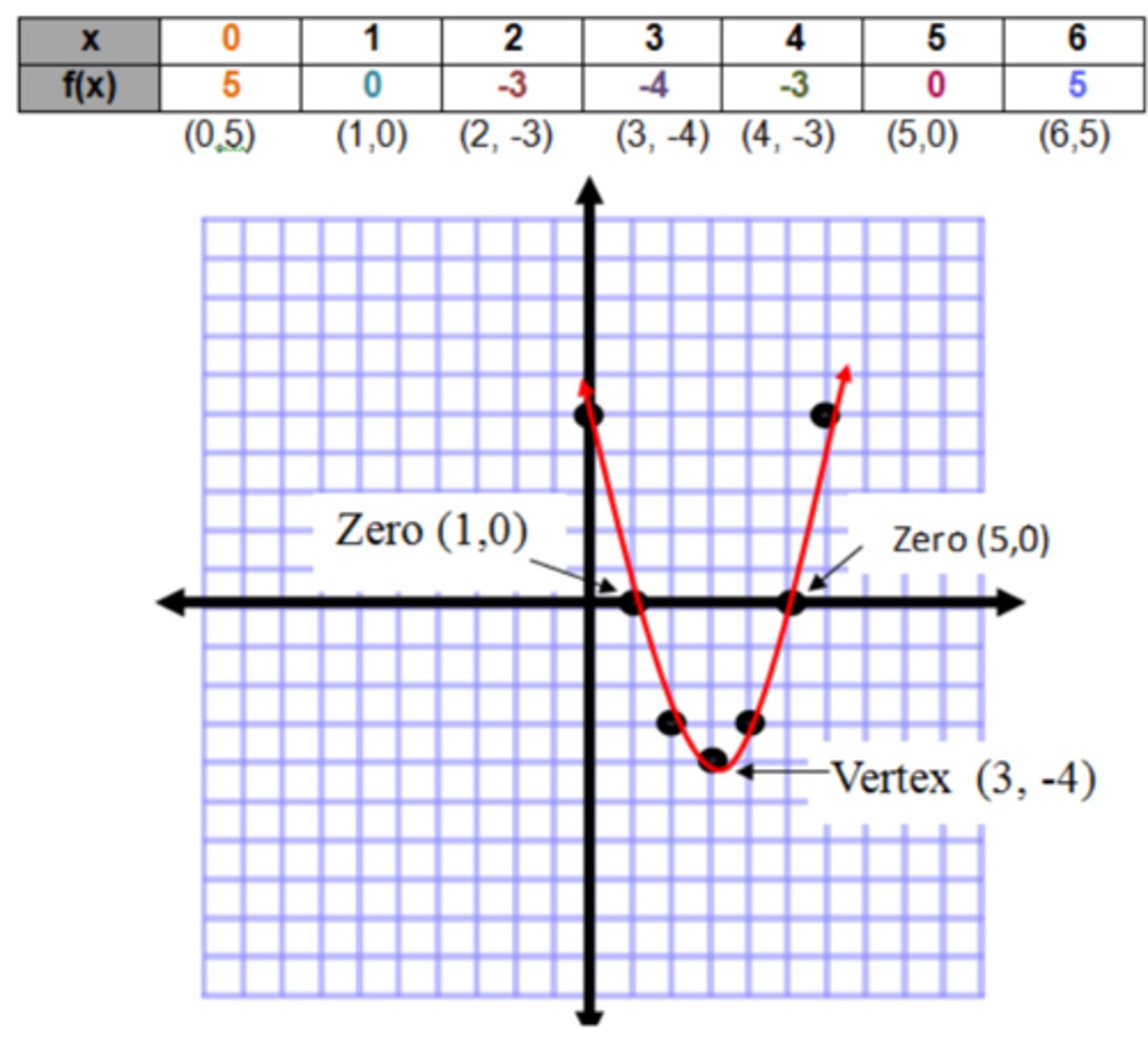
Graph a parabola using a table

words for "<"

is less than, is smaller than, shade below, shade to the left

words for ">"

is more than, is greater than, is larger than, shade above, shade to the right

in y = mx + b, "m" stands for?

slope

in y = mx + b, "b" stands for?

the y-intercept

changing the "m" in the slope-intercept form of the equation of a line changes what?

the steepness of the line

changing the "b" in the slope-intercept form of the equation of a line changes what?

moves the line up or down the y-axis.

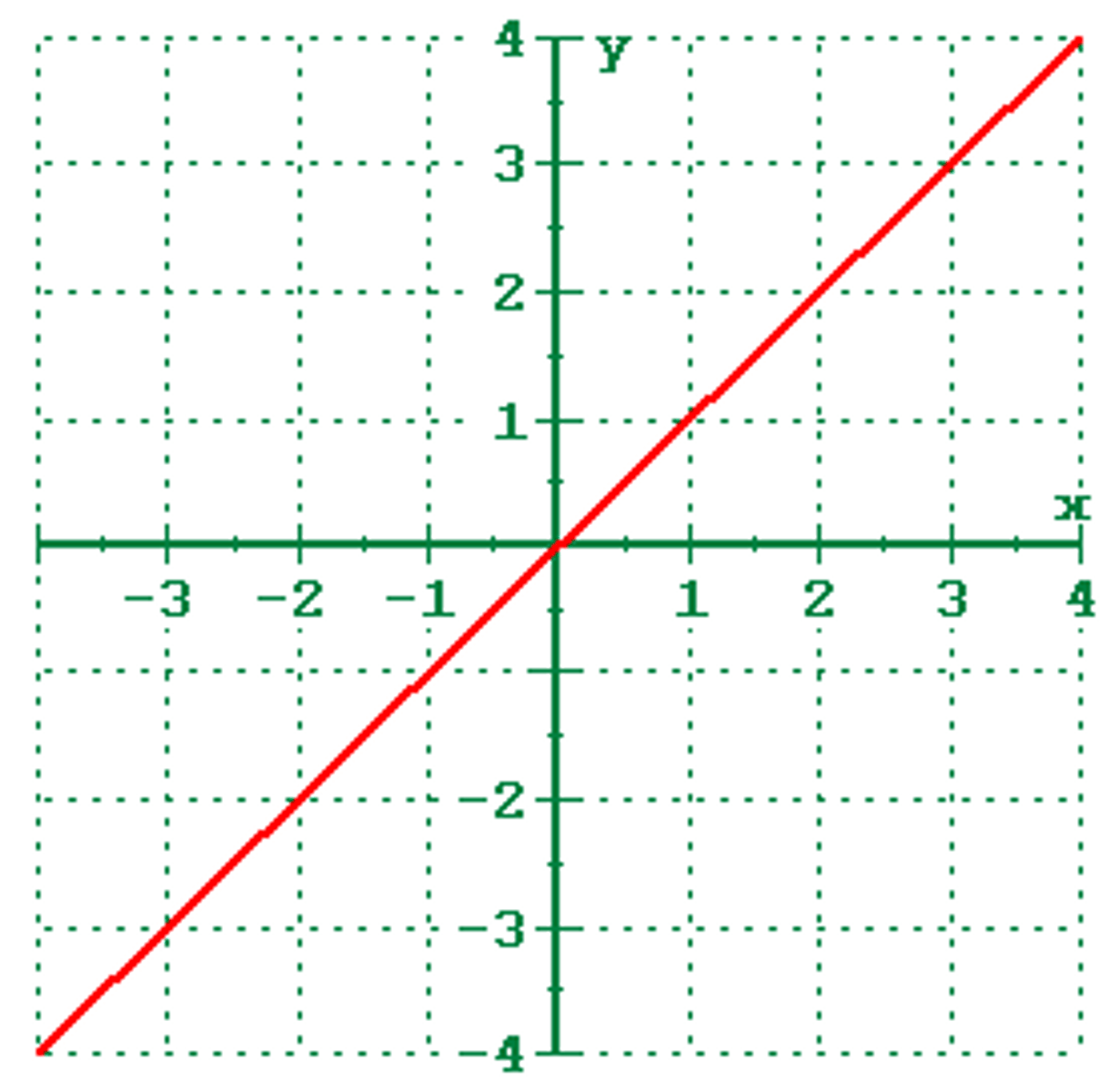
what is the linear parent function?

y = x

f(x) = x

define slope

the steepness of a line, vertical change/horizontal change, (y-y)/(x-x), rise over run

how is slope important for linear equations and lines?

linear equations and lines have CONSTANT slopes. The slope is the SAME all the way up and down the line.

what slope does a HORIZONTAL line have?

slope = 0

what slope does a VERTICAL line have?

undefined slope

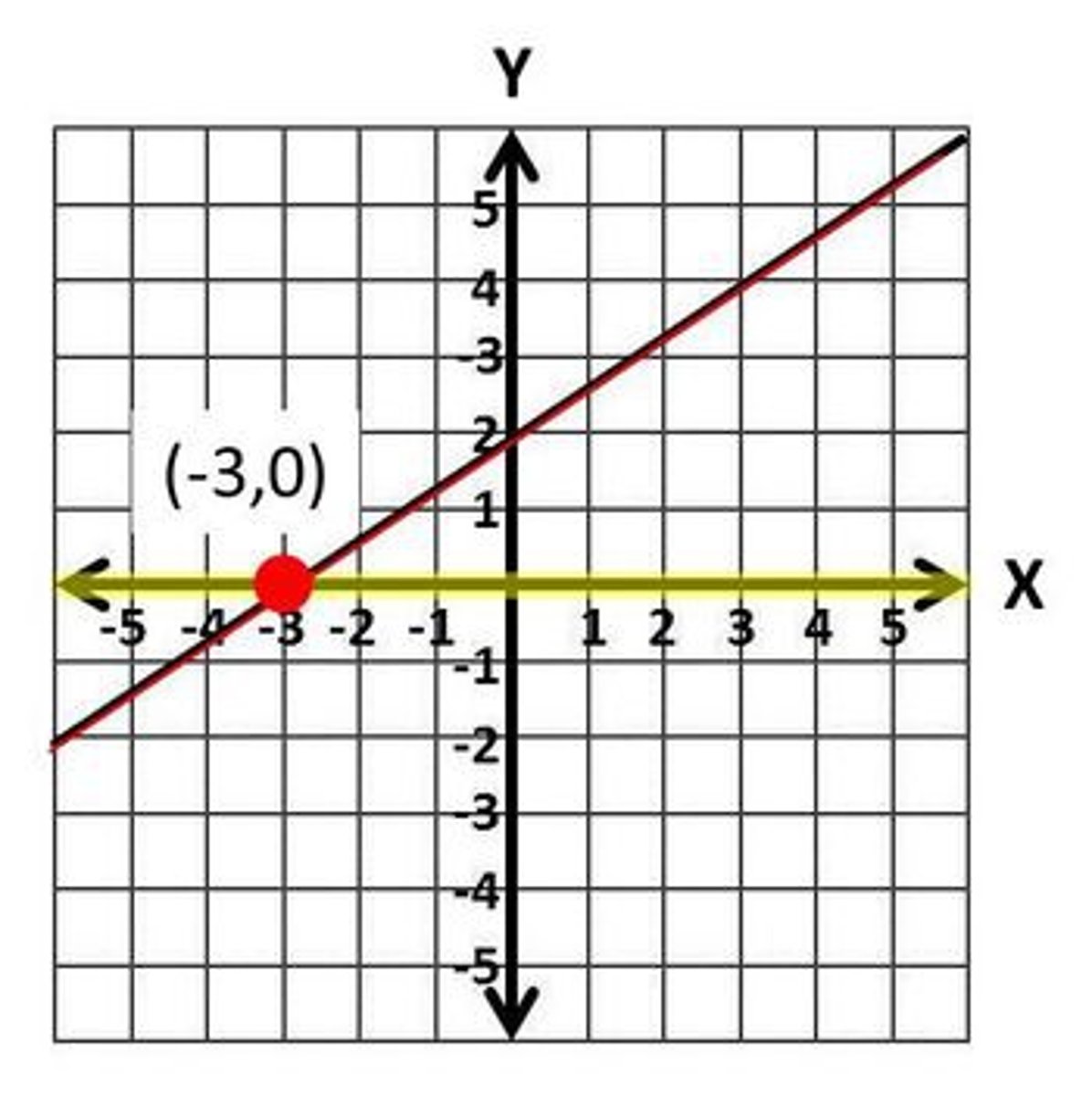
what is the x-intercept?

the point where the graph crosses the x-axis. It has the coordinates (x, 0)

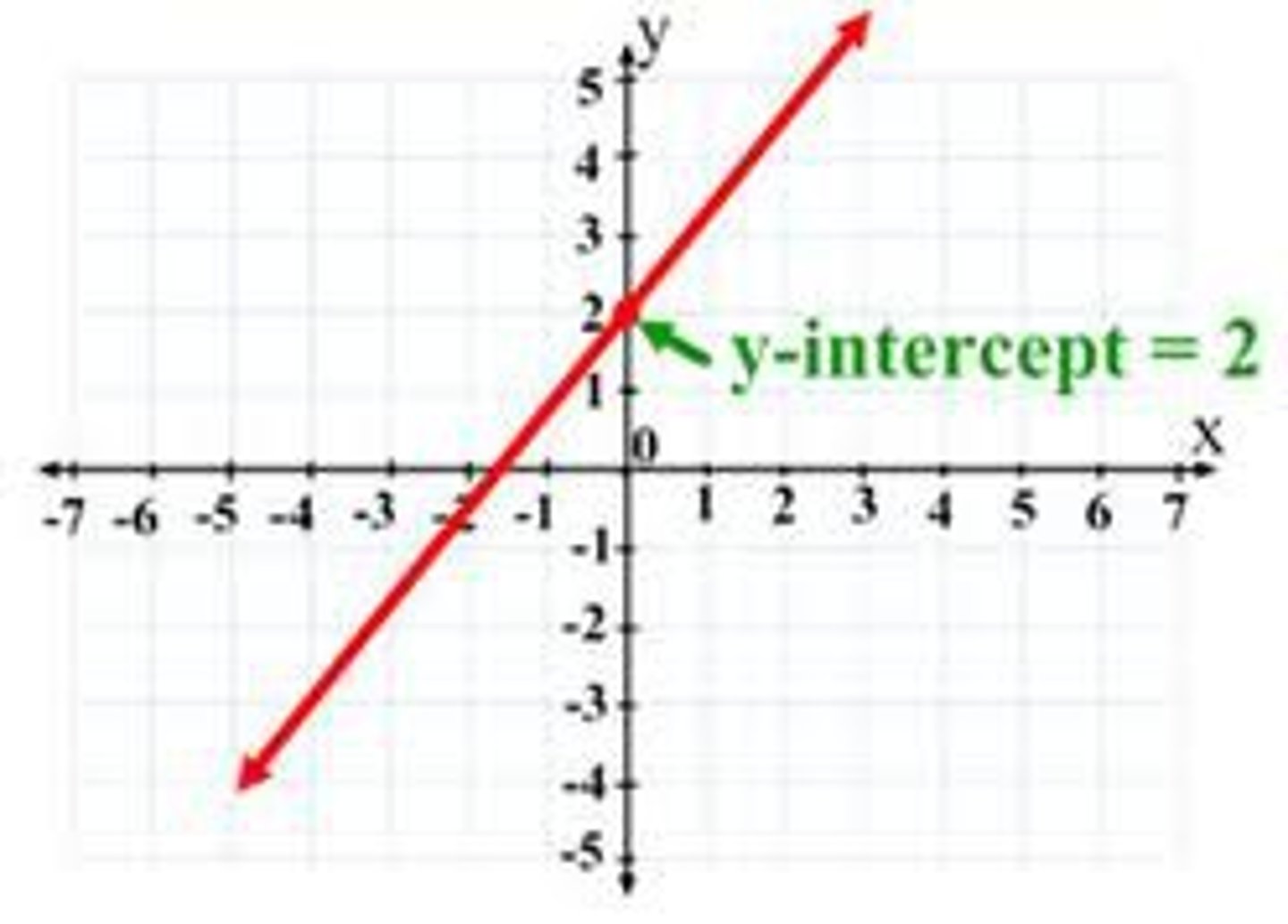
what is the y-intercept?

the point where the graph crosses the y-axis. It has the coordinates (0, y)

What is Direct Variation?

y = mx, or y = ax, or y = kx. m, a, or k is just the coefficient in front of the x. They are also the SLOPE of the direct variation line. Direct variation lines have a y-intercept ot (0, 0)

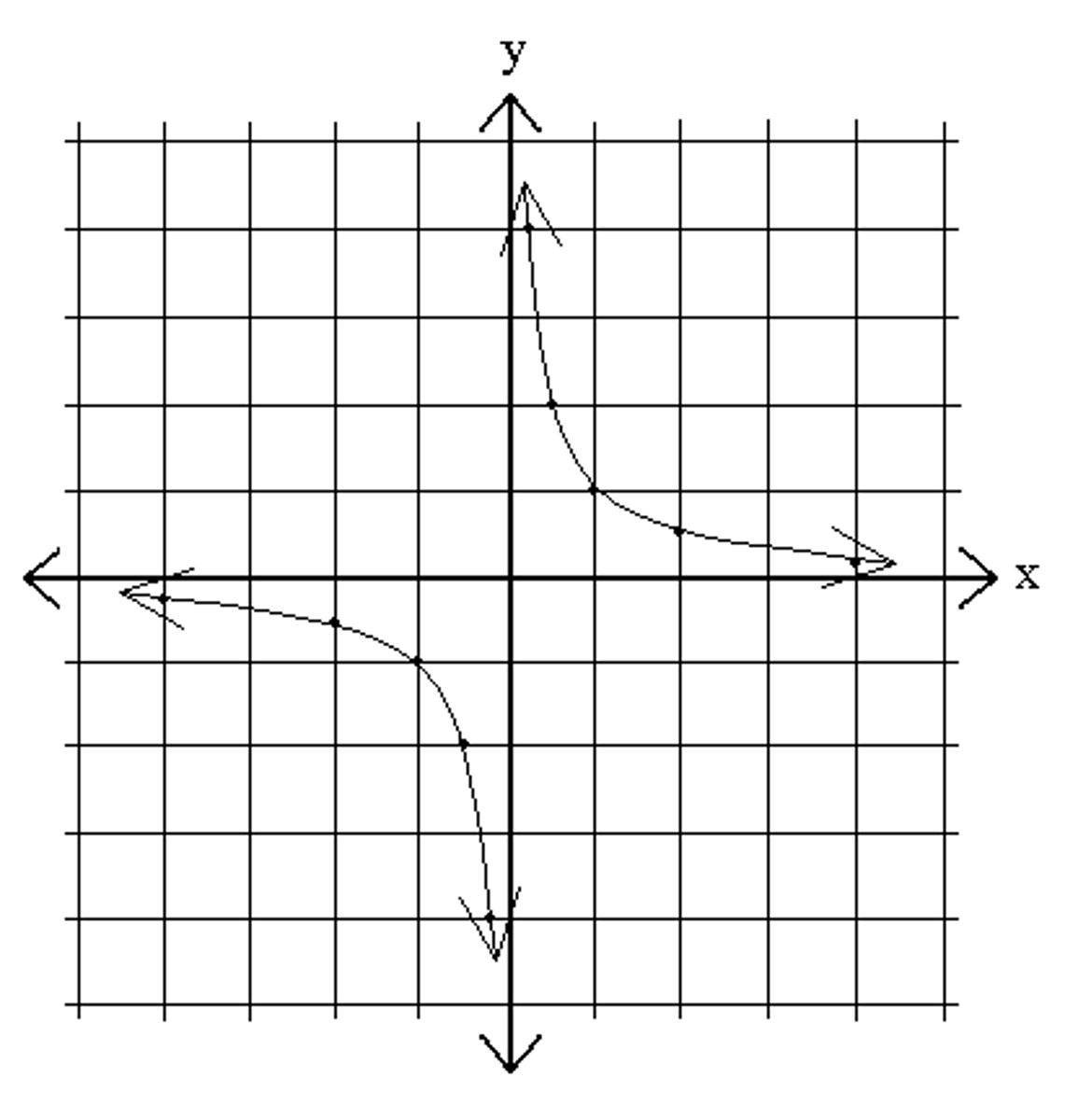
What is Inverse Variation?

y = 1/x. As one quantity increases, the other decreases

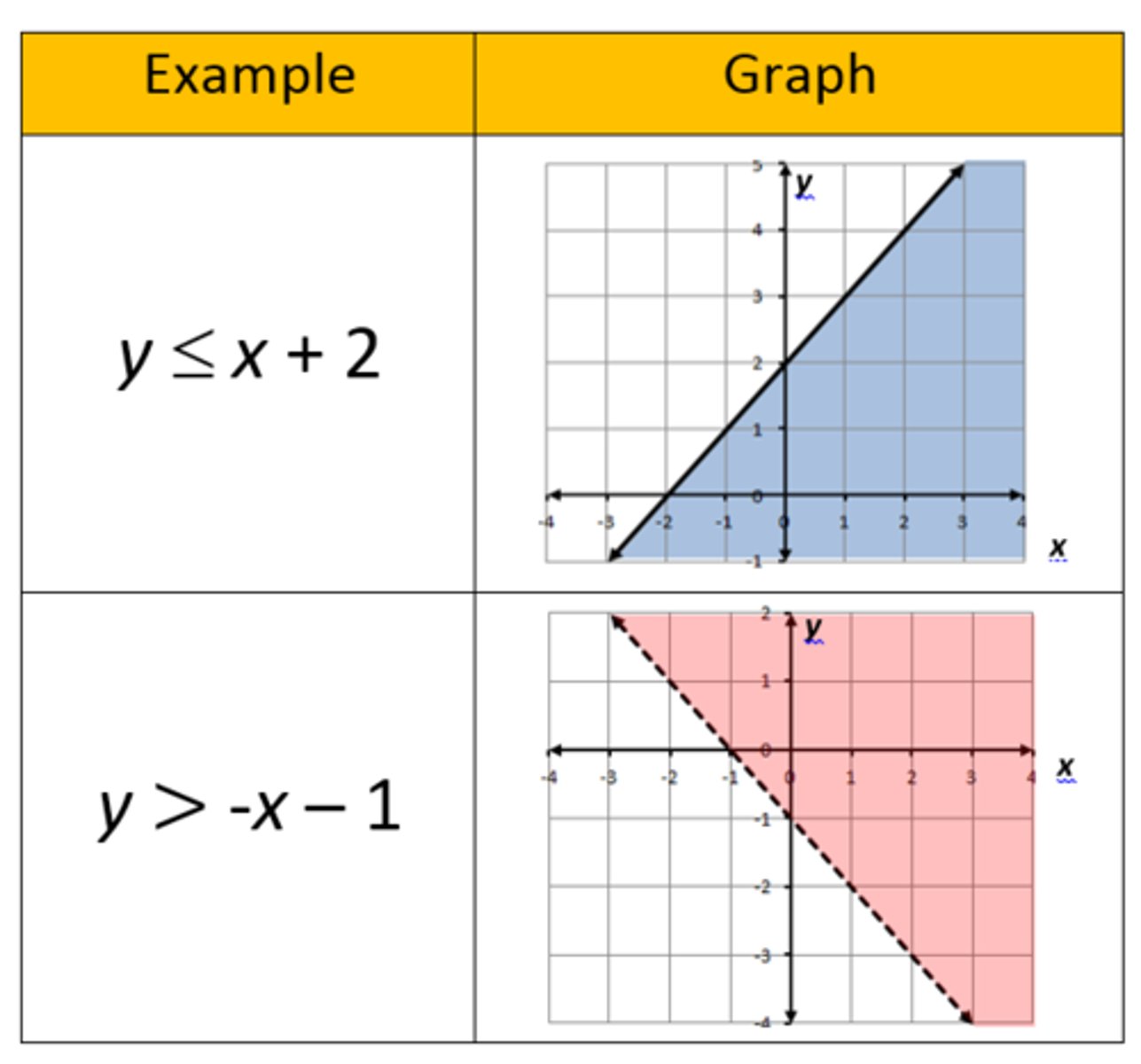
what is a linear inequality?

It is an equation with a <, >, < or =, > or = in the place of the =.

How do the slopes of parallel lines compare?

They are the same

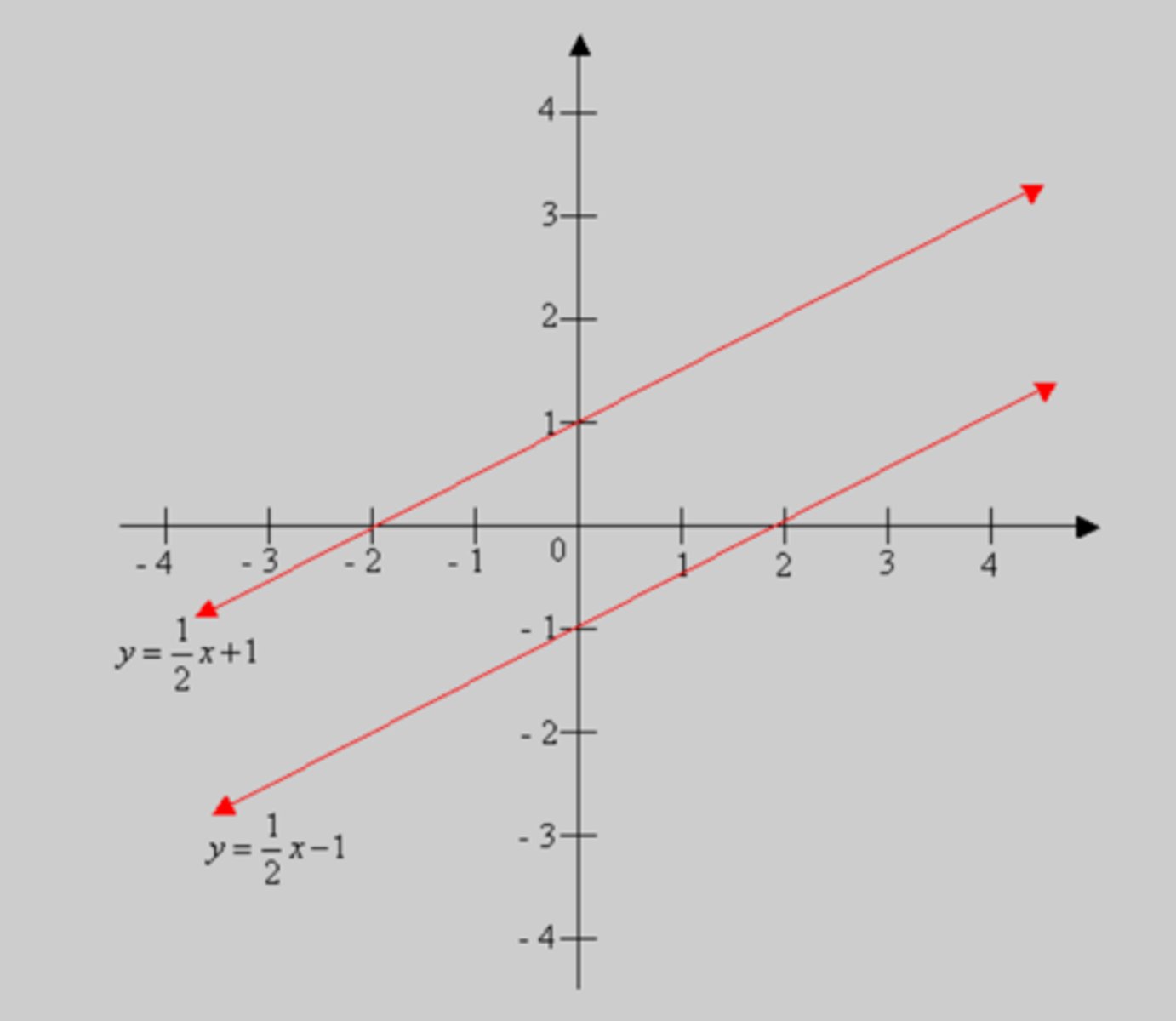
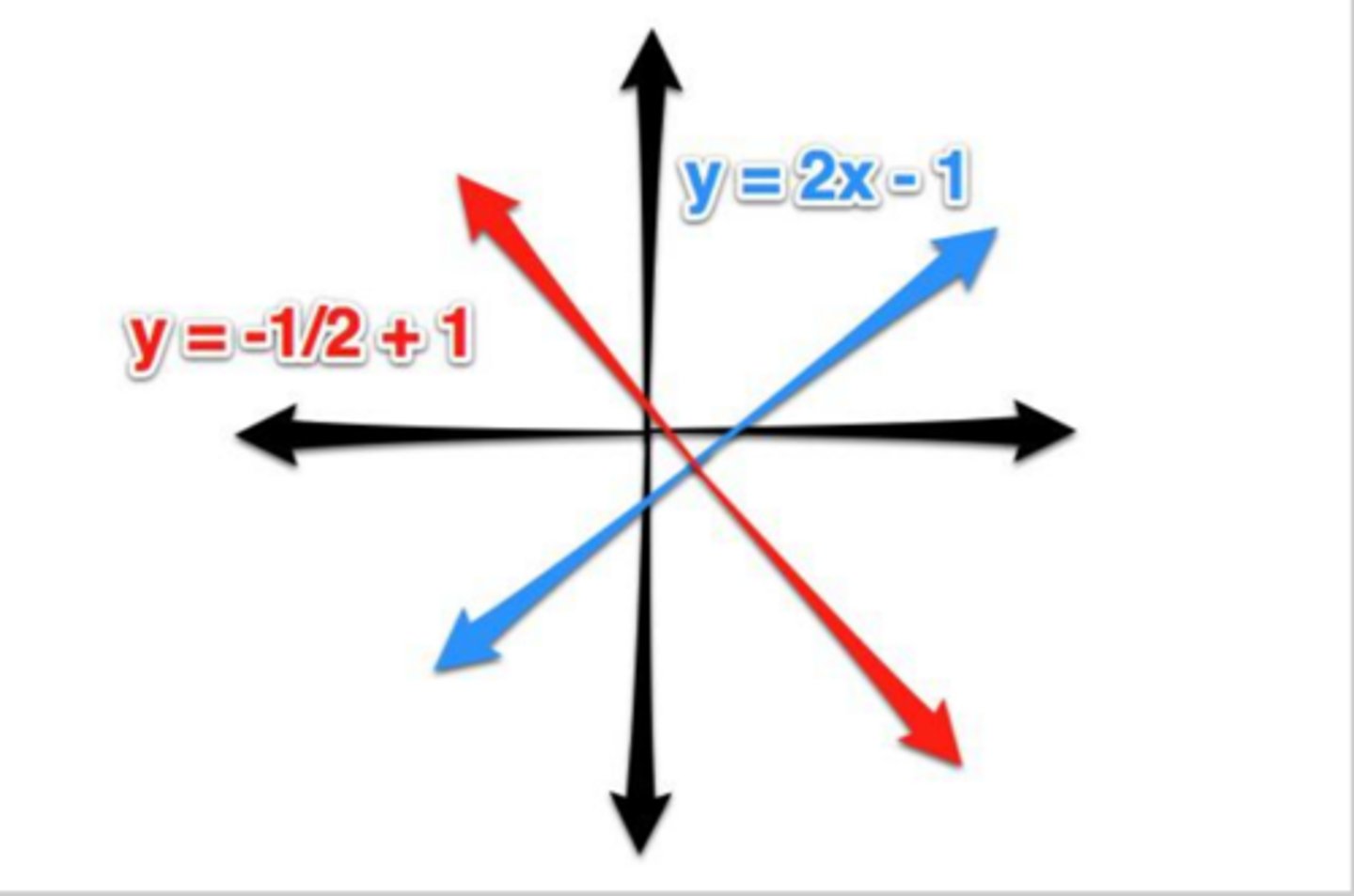
How do the slopes of perdendicular lines compare?

They are opposite and fraction is flipped. Example: lines with the slopes -2 and 1/2 are perpendicular.

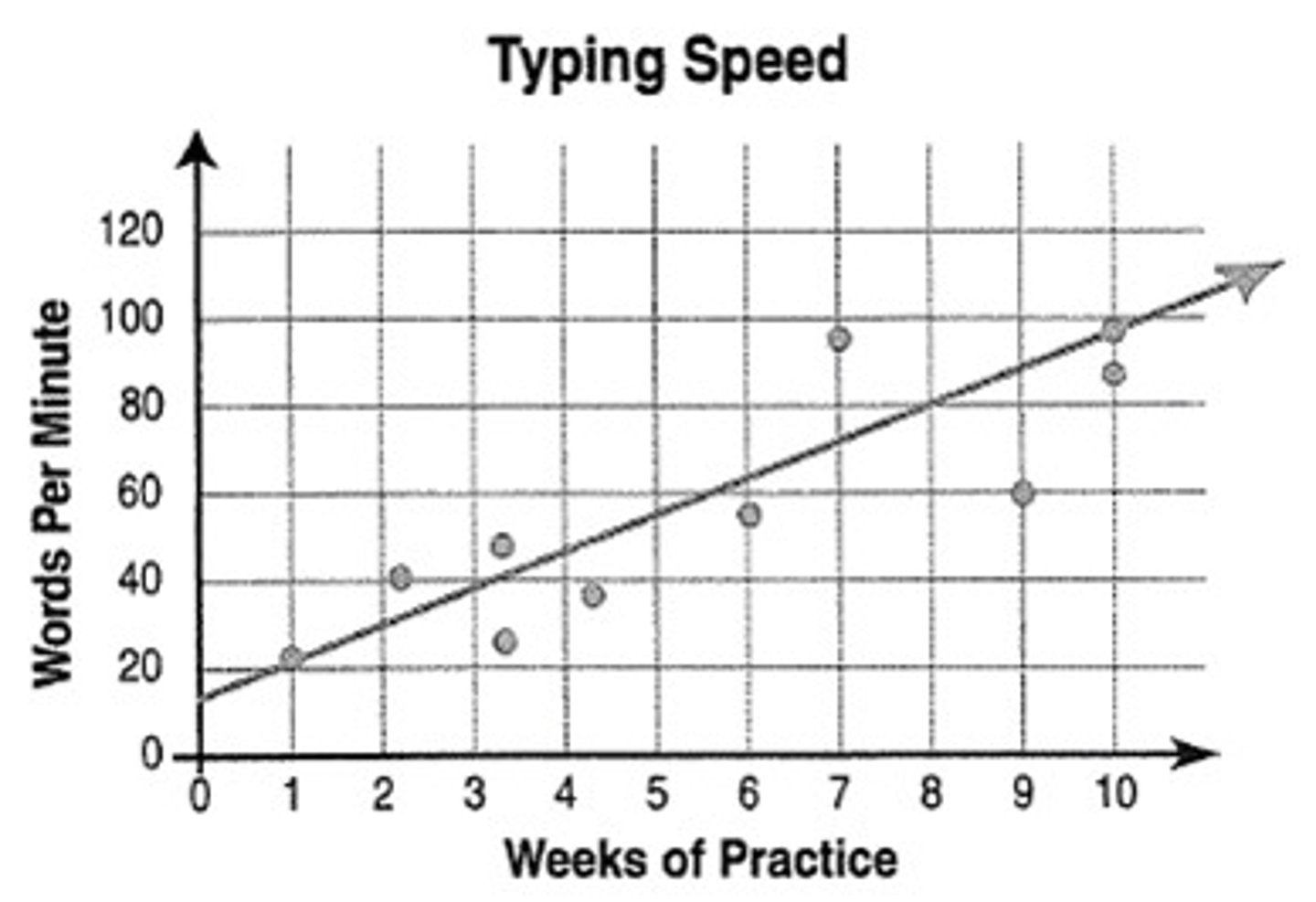
What is a line of best fit?

A line drawn through the points on a scatterplot to estimate the best line through the data.

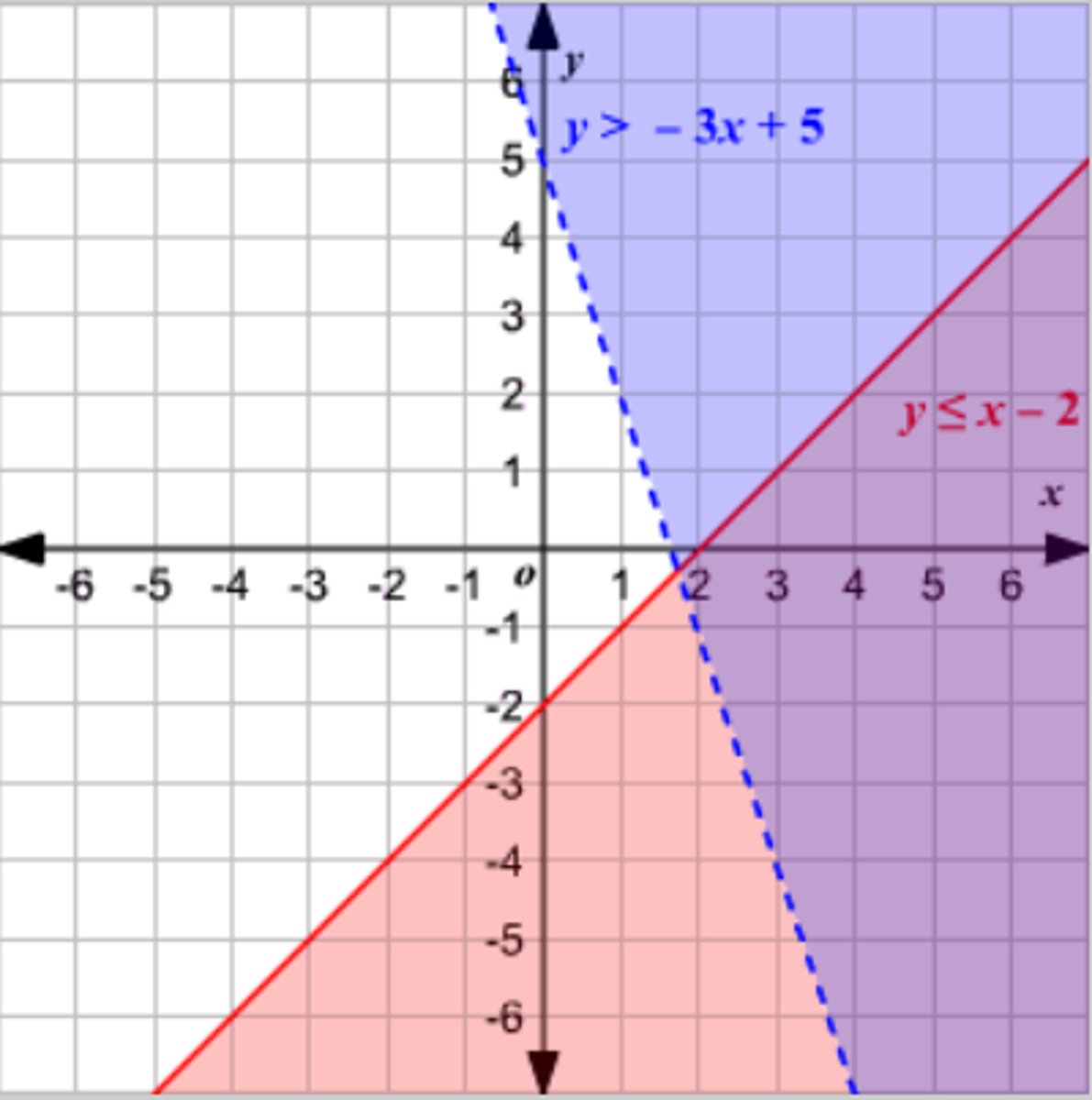
What is a system of equations or system of inequalities?

2 or more equations or inequalities graphed on the same coordinate plane

What is the SOLUTION of a system of equations?

where the lines touch or cross

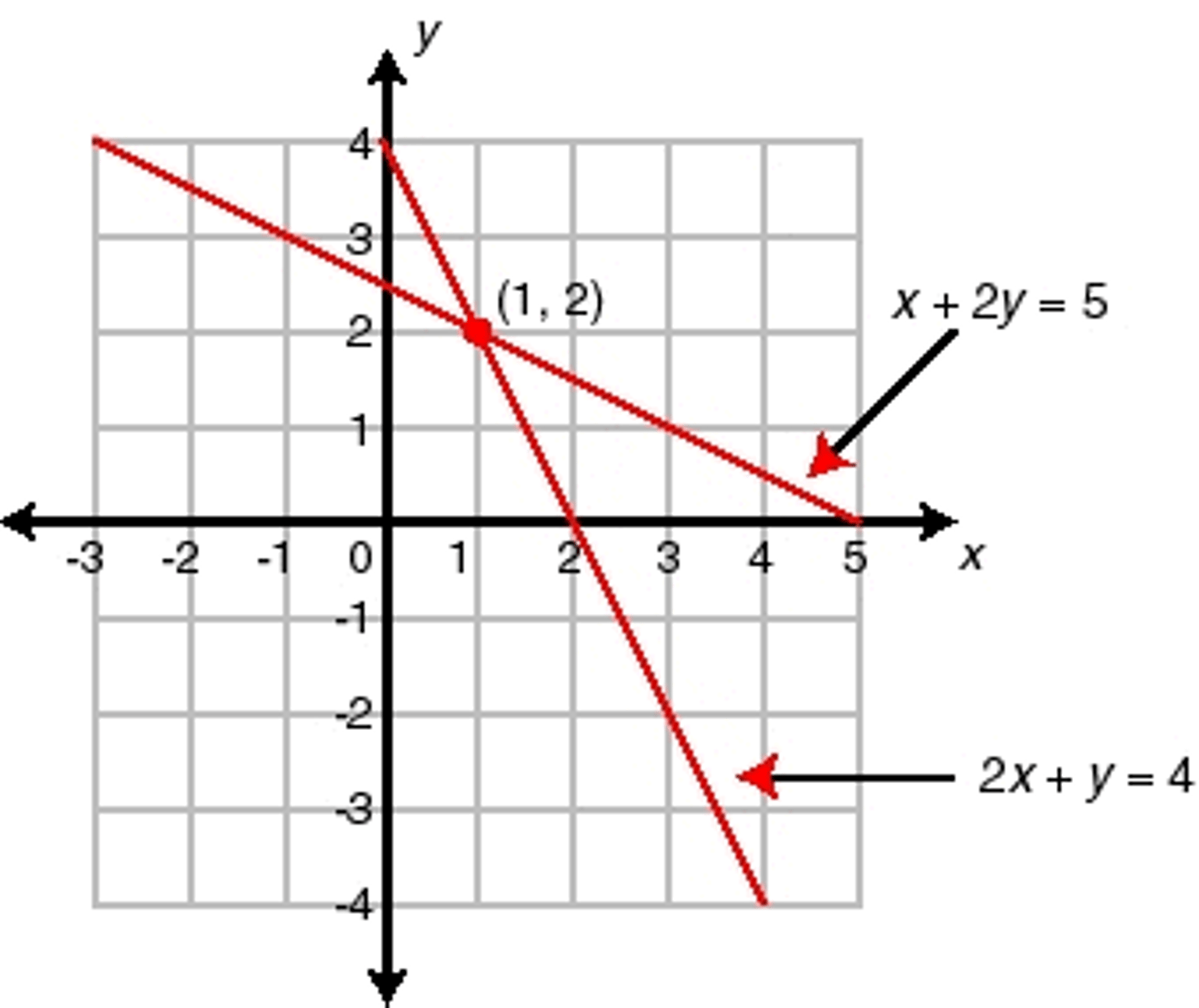
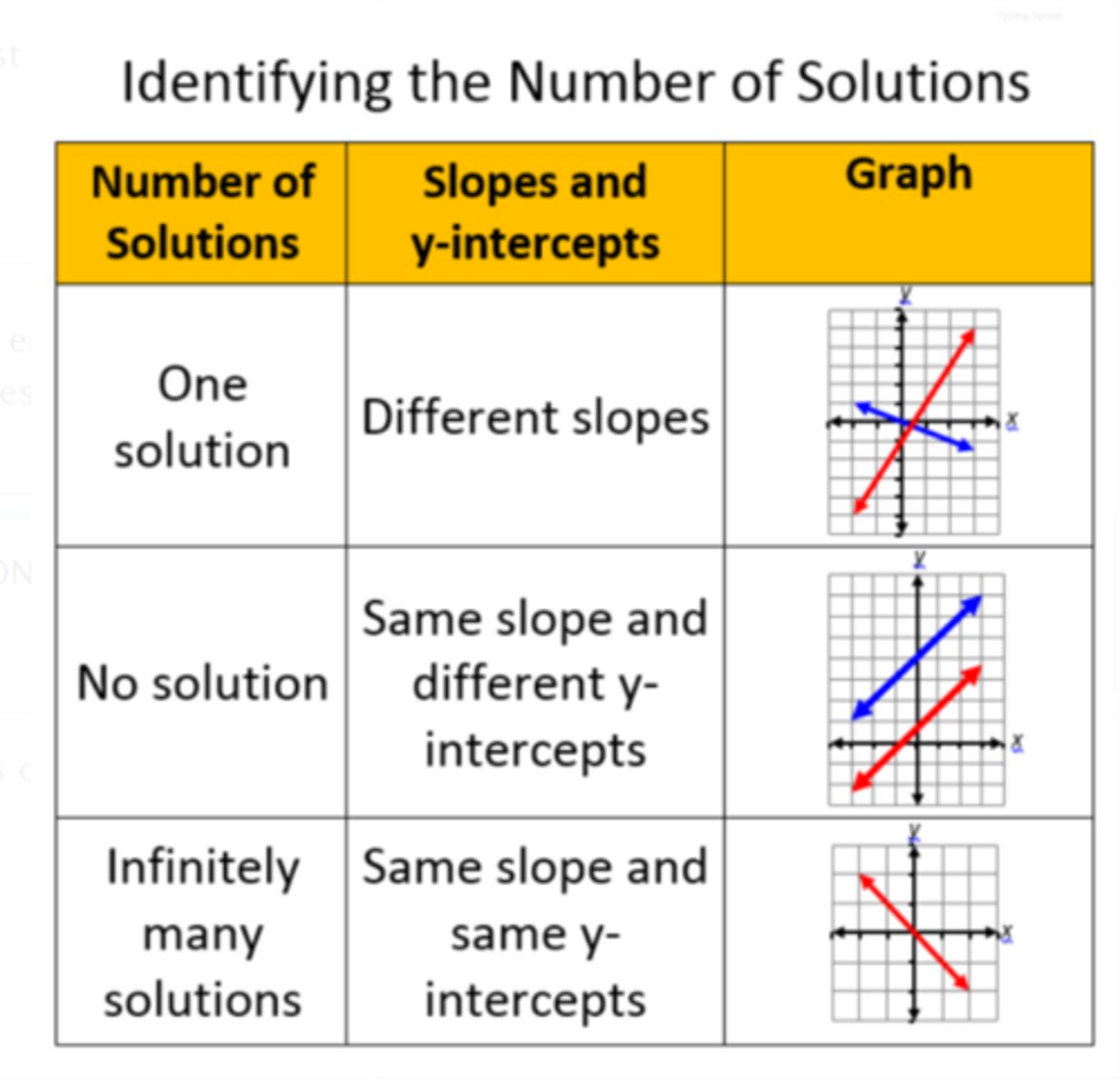
How many solutions can a system with 2 equations have?

1) no solutions, if the lines are parallel and have the same slope. 2) one solution, if the lines intersect at one point. 3) infinite many solutions, if the two equations are the same and touch each other everywhere.

What is a quadratic equation or function?

an equation of function that has "x-squared" as its highest order exponent.

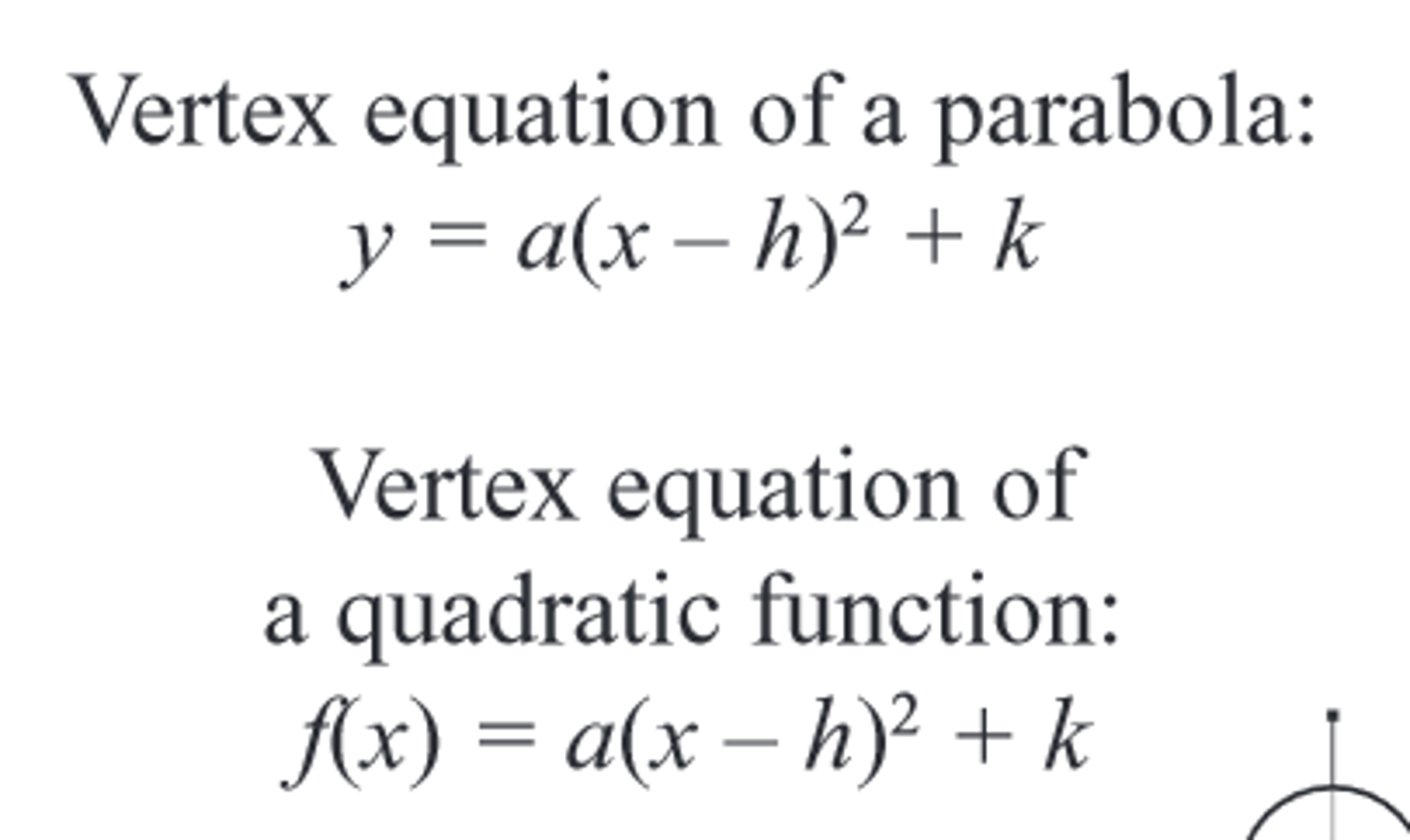
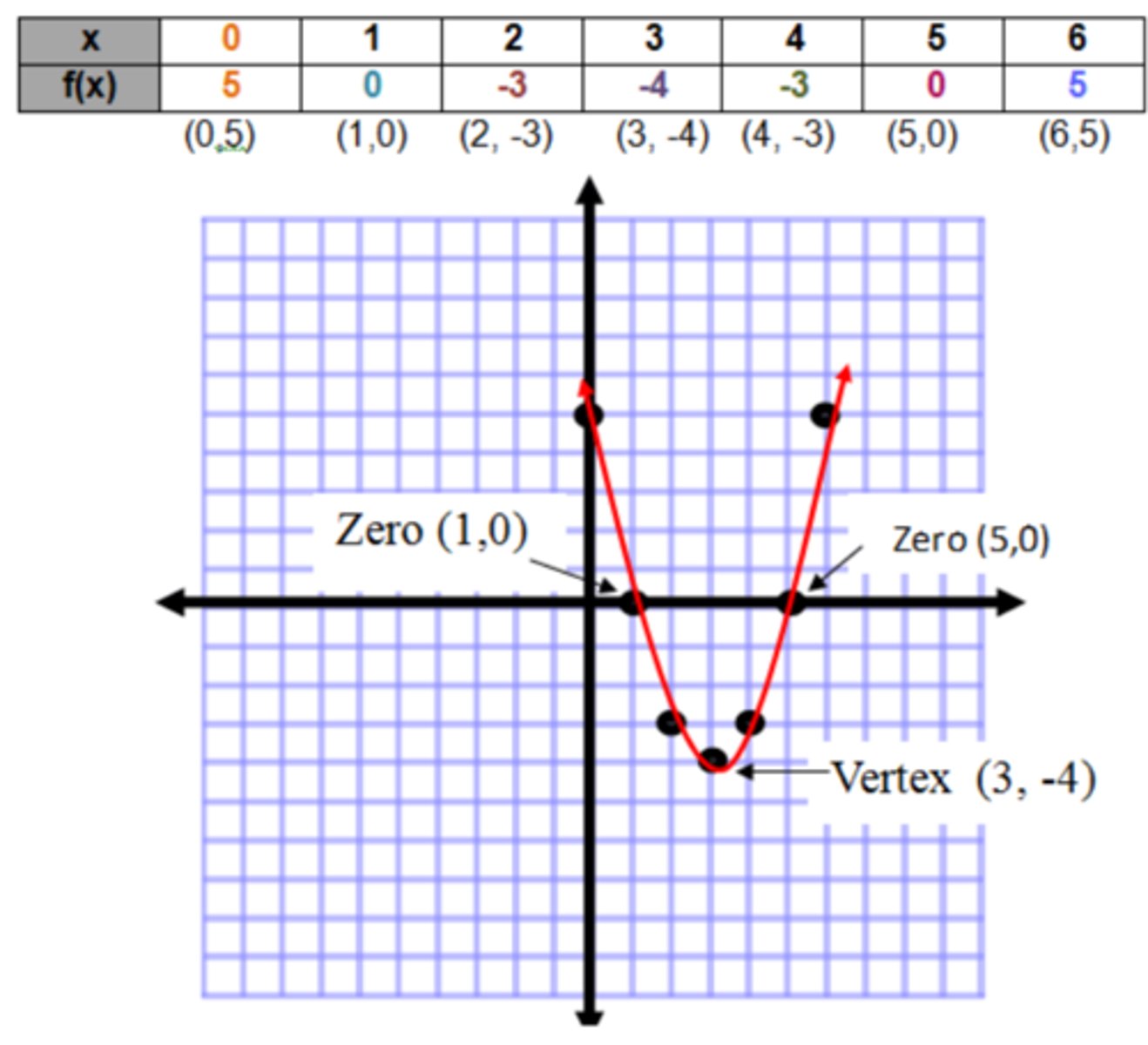
Where are the solutions of a quadratic function?

at the x-intercepts. They are also known as zeros and roots.

What are "like terms"?

mathmatical terms that have the SAME variables raised to the SAME exponents.

How do you combine like terms?

Add their coefficients.

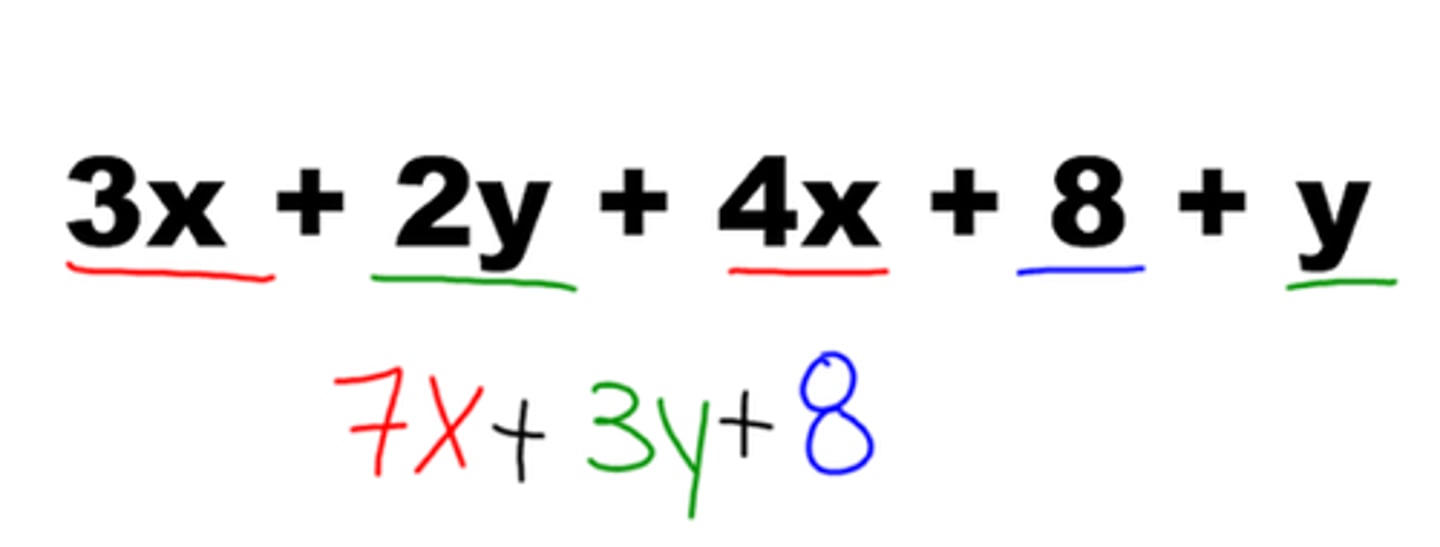
How do you MULTIPLE exponents of like variables?

ADD them

How do you DIVIDE exponents of like variables?

SUBTRACT them

What is the "rate of change" on a graph?

Slope

Mean (Average)

Add up all the data points, then divide by however many data points there were. Ex. 3,6,9

3+6+9= 18 /3 = 6

Median

When the data is put in order from smallest to largest, it is the number in the middle. If there are two numbers in the middle, you add them together then divide by 2. (You take their average)

Mode

The number that shows up the MOST

Range

When talking about data sets, make sure the numbers are in order from smallest to largest, to find it you SUBTRACT the smallest from the largest.

Integer

A whole number, both positive and negative numbers, including zero.

... ,-3, -2, -1, 0, 1, 2, 3, ......

Whole numbers

Start with 0, 1, 2, ......

Natural numbers

Counting numbers: 1, 2, 3, ......

How do you Add and Subtract FRACTIONS?

You have to have a common denominator.

How do you multiply FRACTIONS?

Cancel or reduce if possible, then multiply straight across. Some people like to multiply straight across and then reduce. Either way, if you can reduce, you MUST REDUCE.

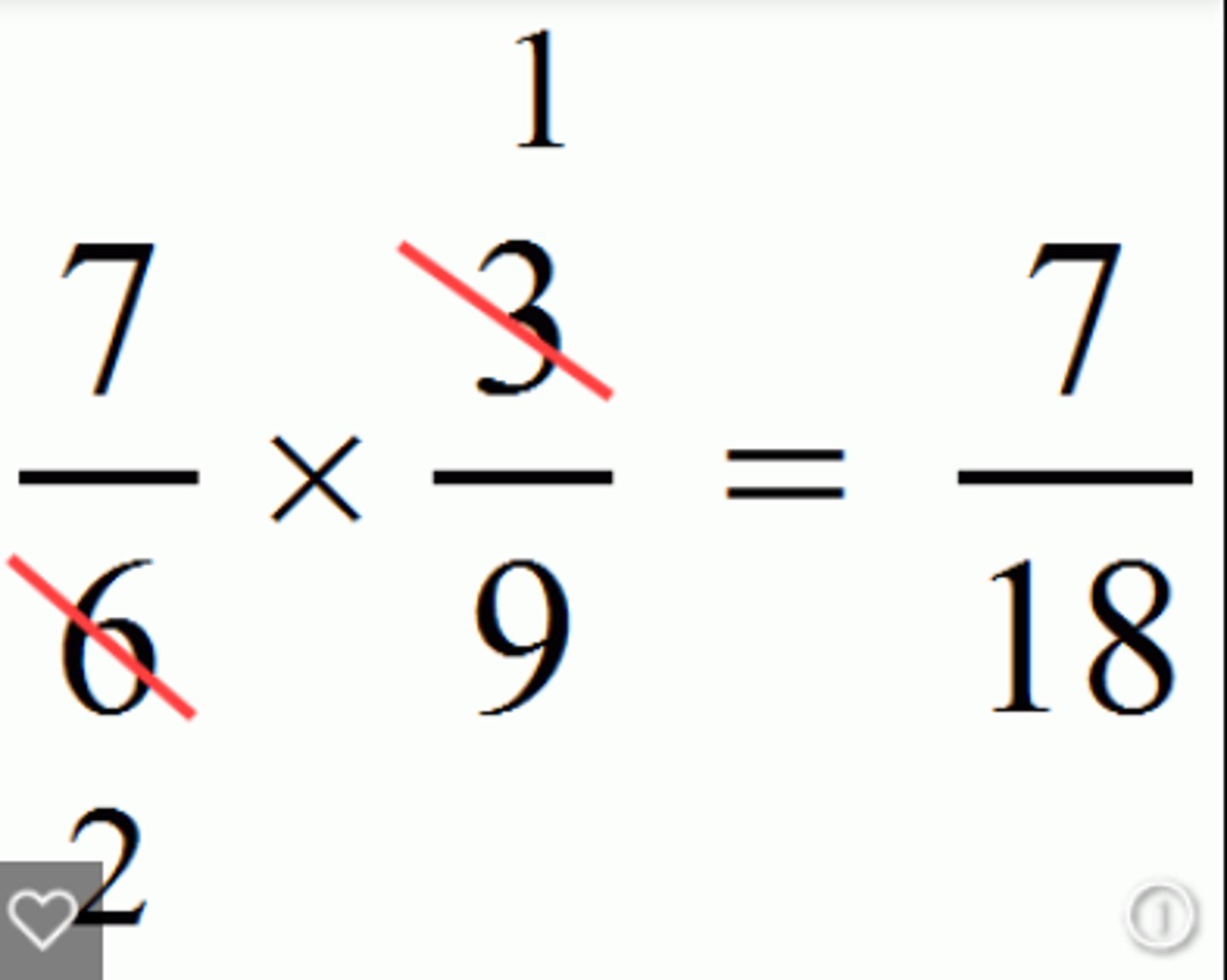
How do you Divide FRACTIONS?

Keep, Change, Flip! Then multiply fractions!

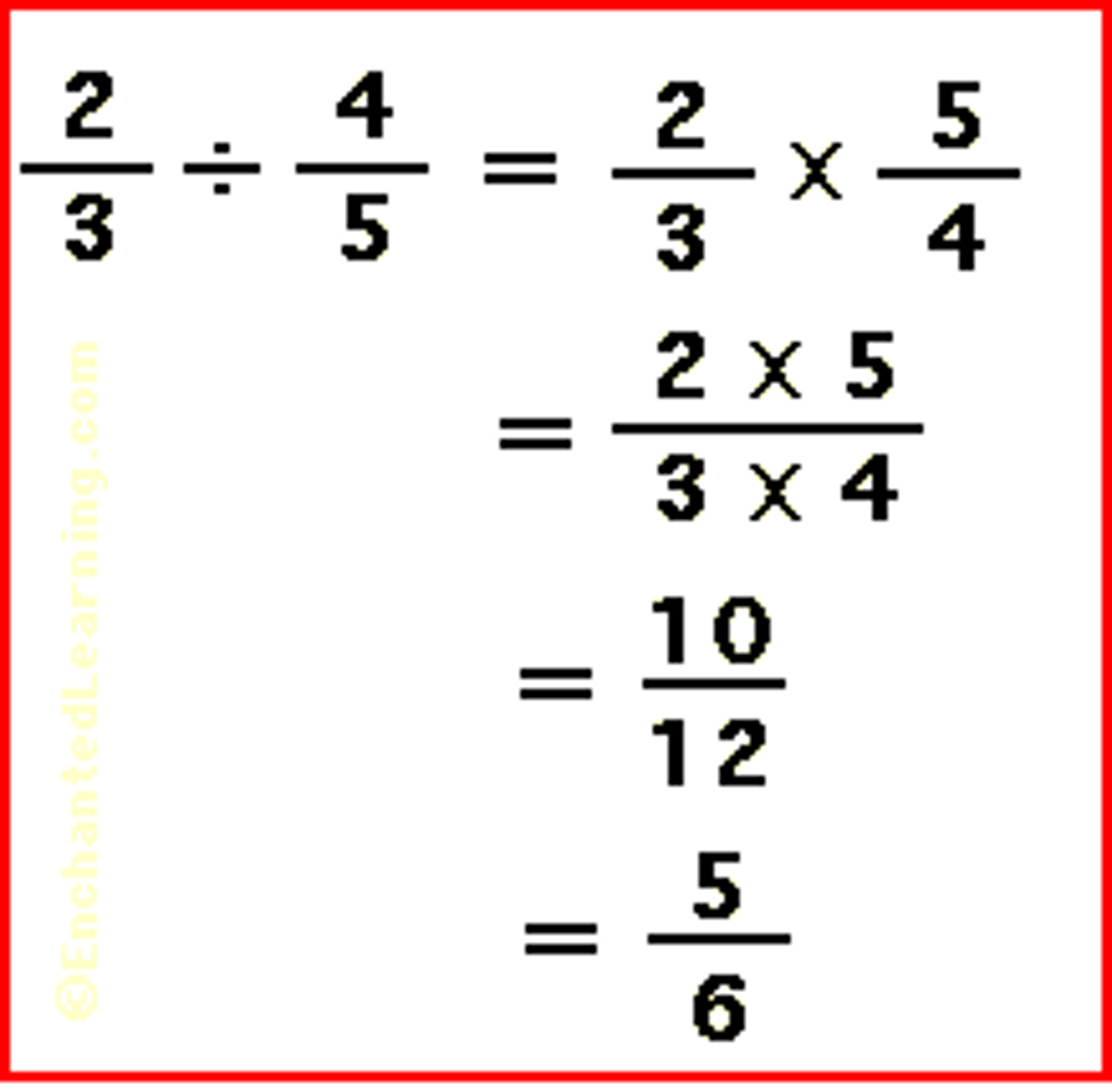
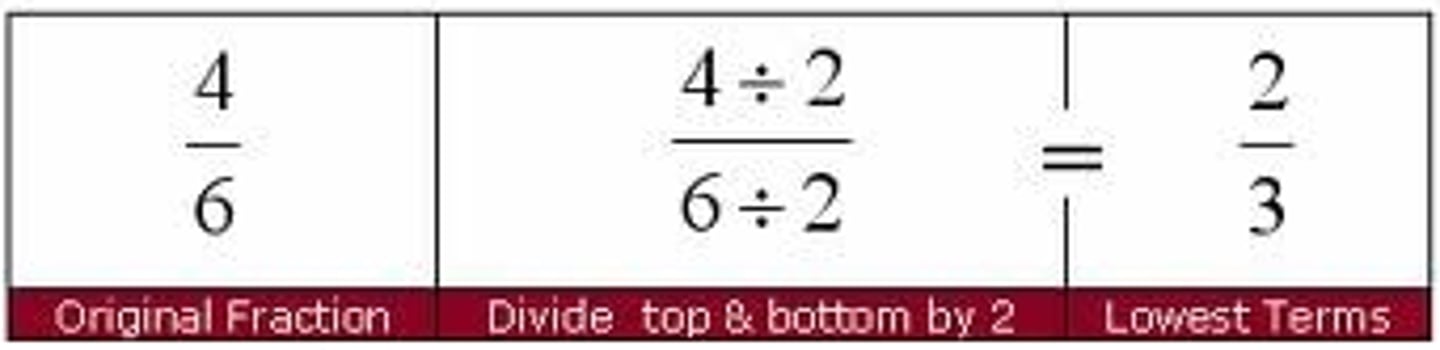
How do you Reduce FRACTIONS?

Find one number that you can divide into both the numerator and denominator that is the same number. Then divide them both by that number.

Quadratic Formula

In standard form, ax^2 + bx + c, where a, b, and c (Just the numbers) can be plugged into the quadratic formula to find the x-intercepts, roots, zeros, or solutions.

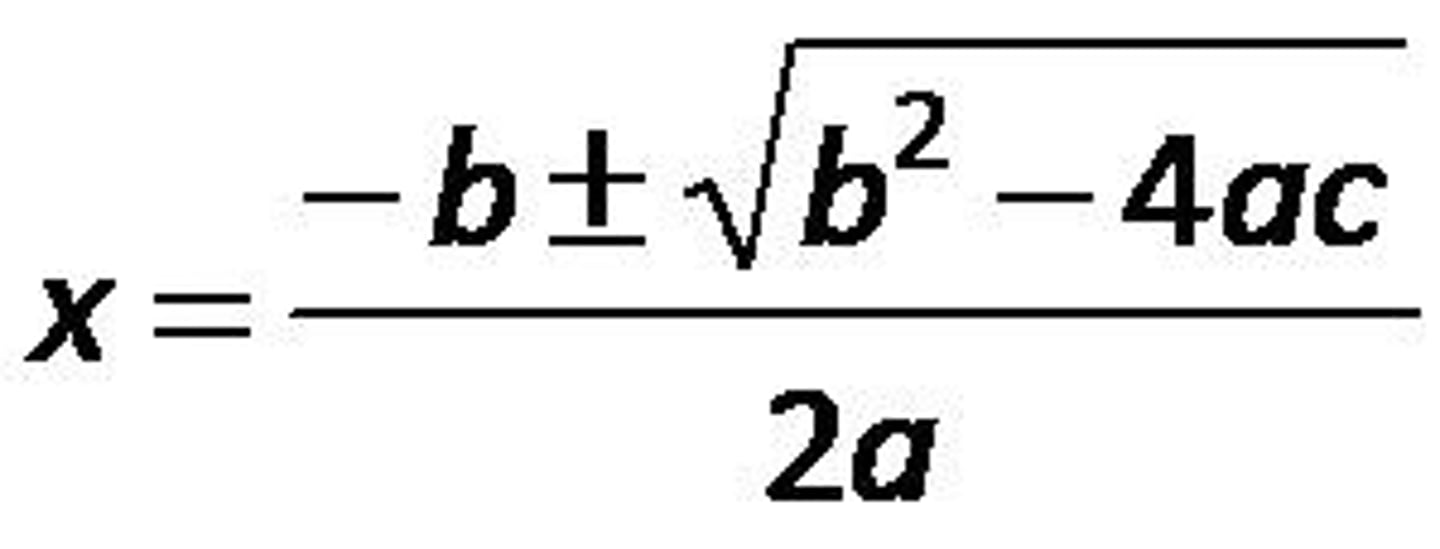
Completing The Square

Isolate x^2 + bx on one side, move the number to the other side of the equal sign. Take b, divide by 2, then square the result. Add that number to both side. It will then factor into a perfect square.

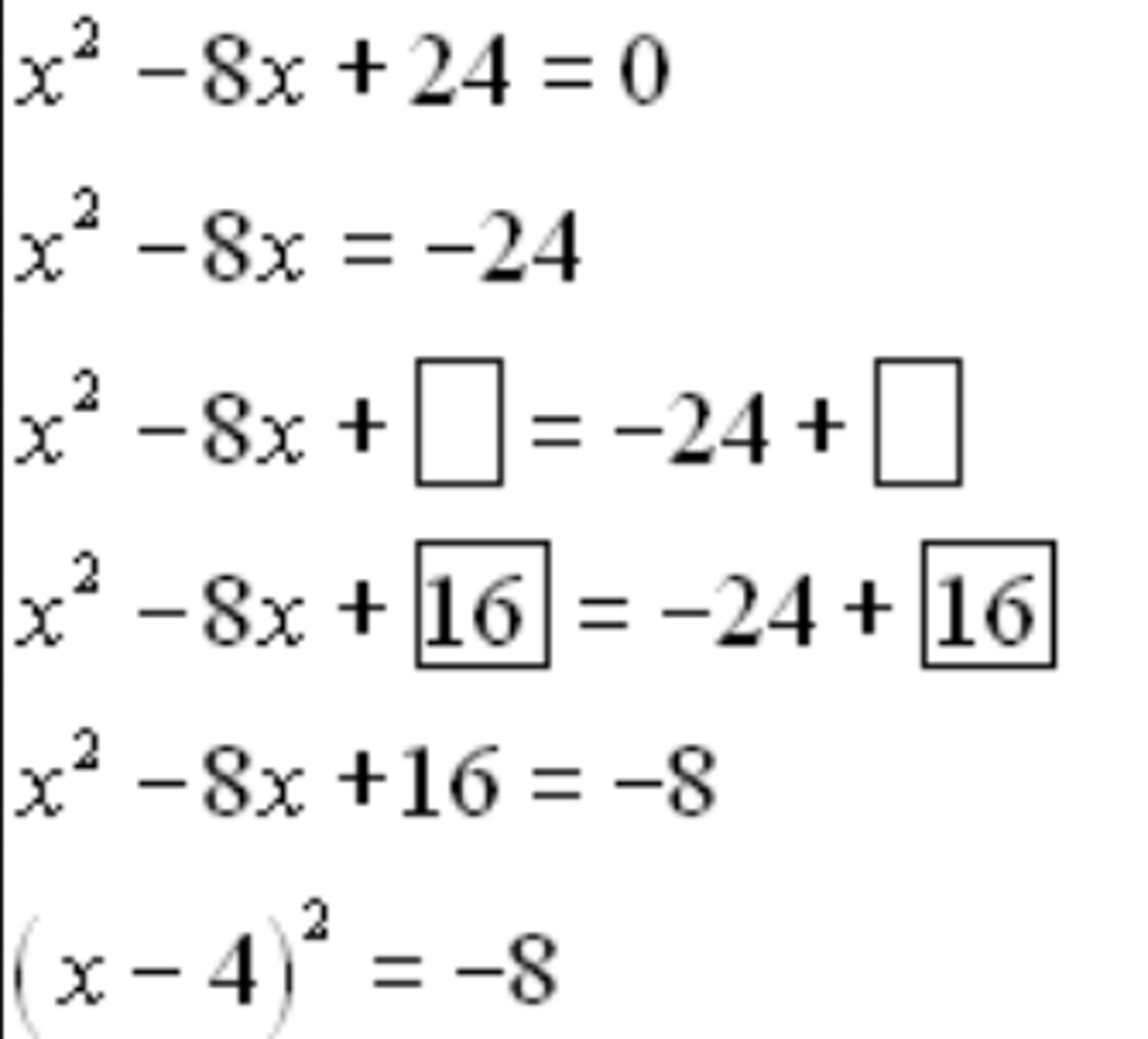
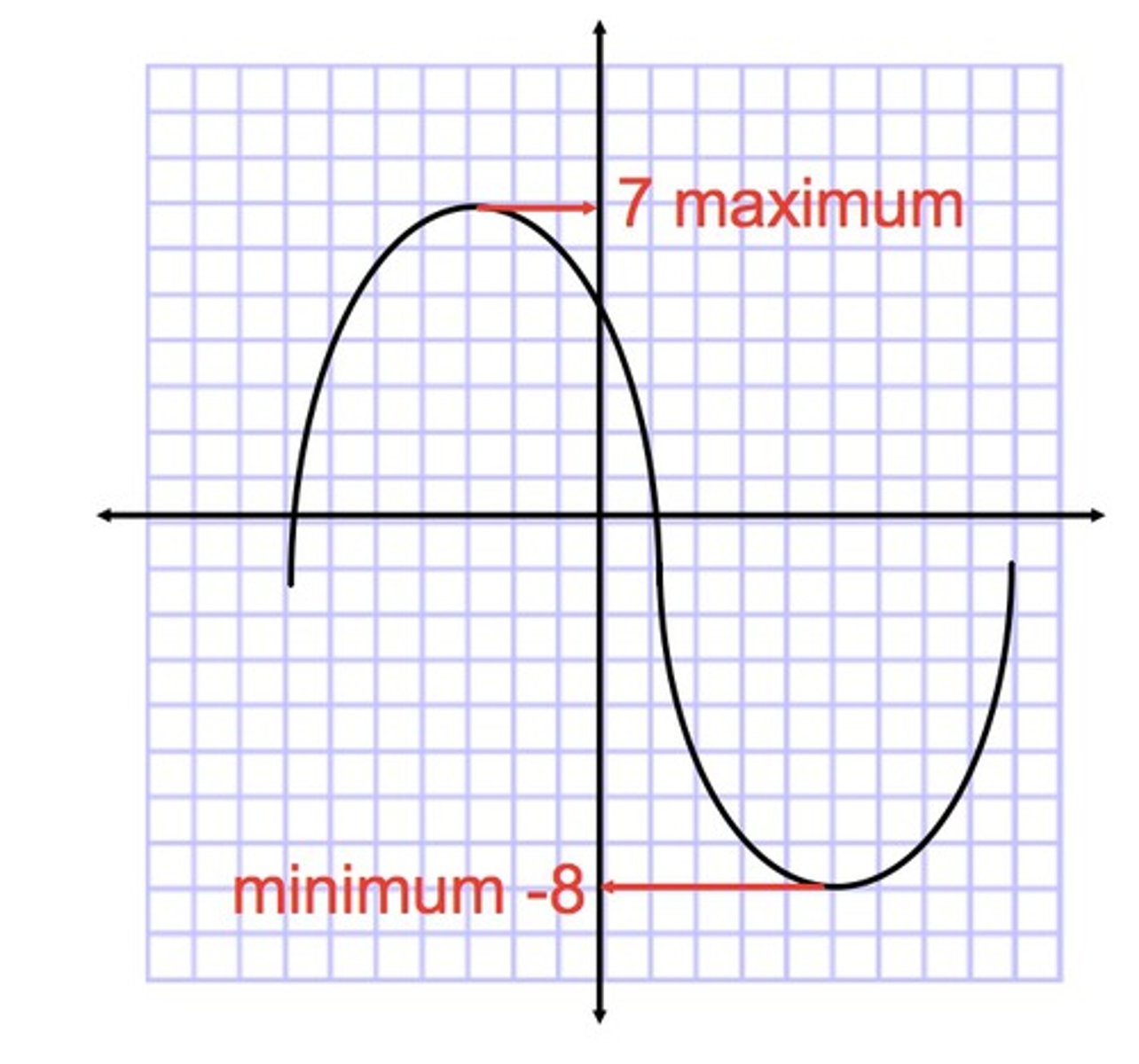
Maximum or Minimum

Maximum is at the highest point of a parabola.

Minimum is the lowest point.

The Square Root Property to solve Quadratics

To get rid of the exponent 2, you can take the square root of both sides. Remember the plus or minus symbol, which can give you two answers.

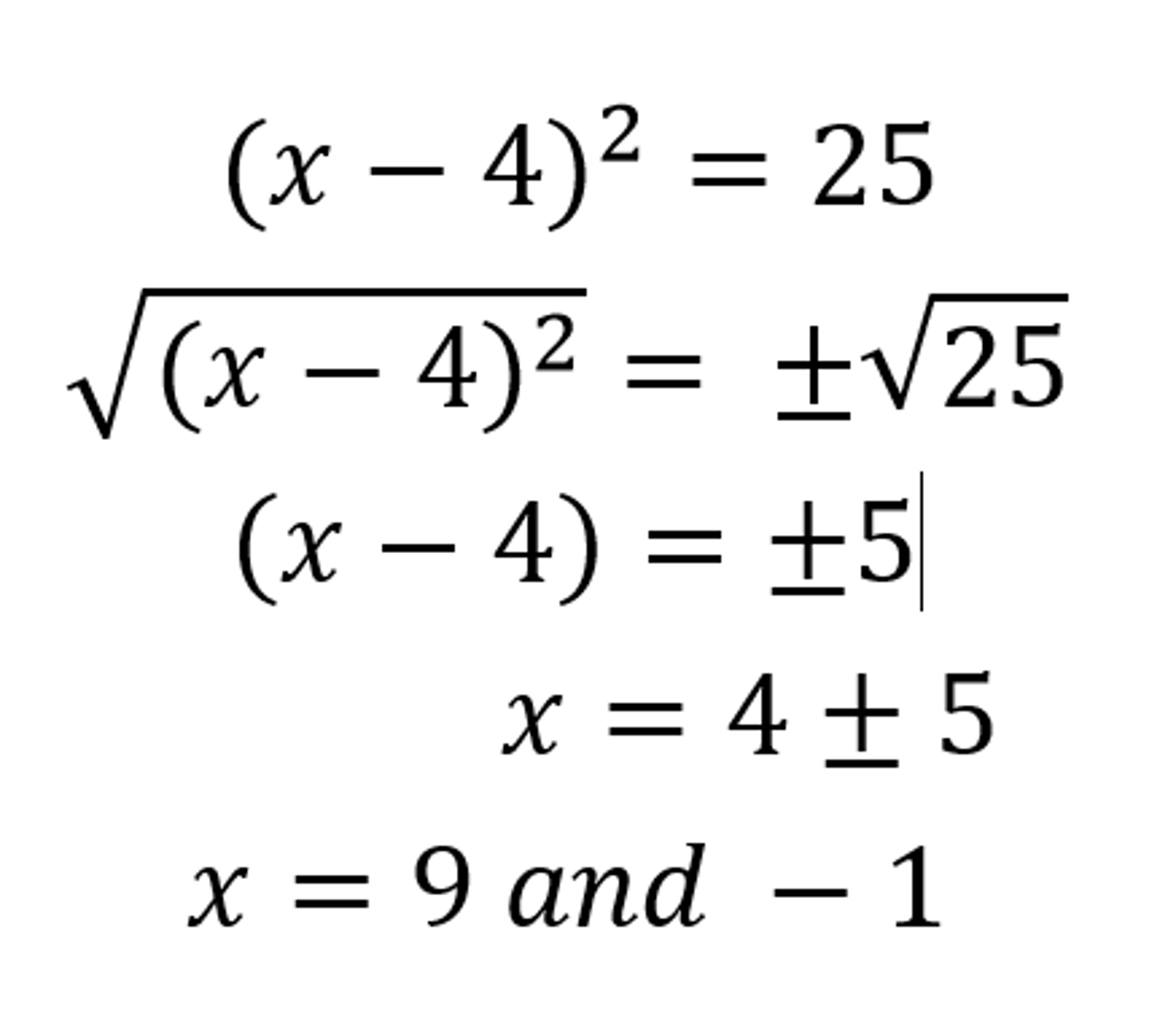
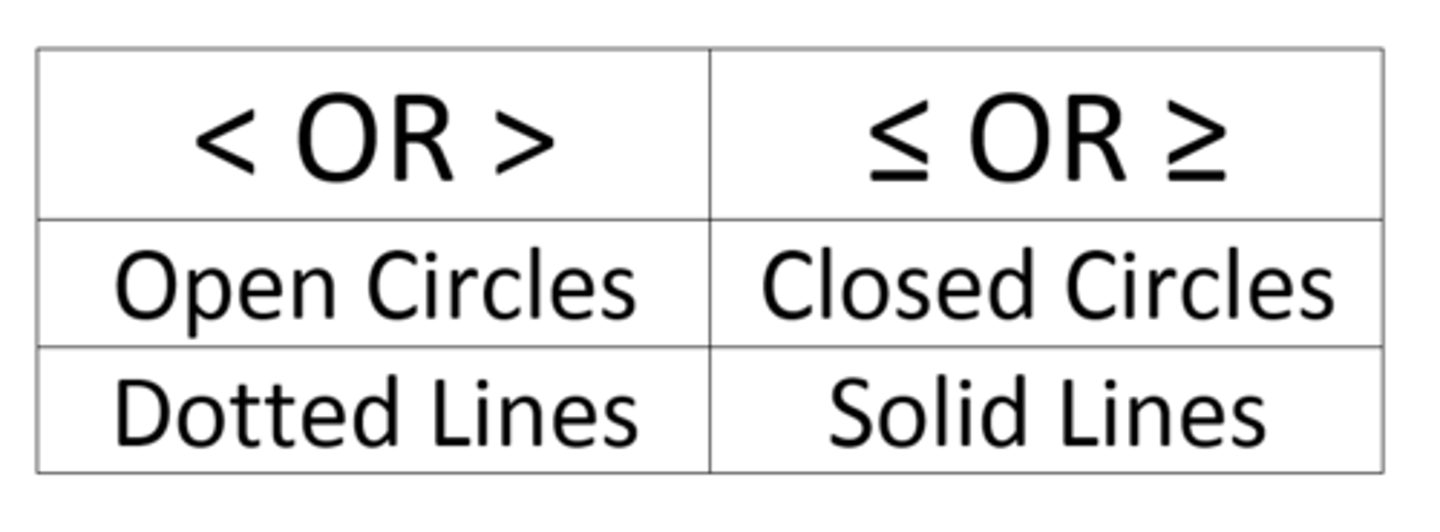
Solid or Dotted Line? Open or Closed Circle?

If it has the line under it (or equal to) it will be a closed circle or solid line.

How to rearrange variables to solve for a specific variable.

Solve A=P+PRT for T. You perform the opposite operation on each variable until you get the one you are solving for all by itself. Subtract P, then divide by P and R.

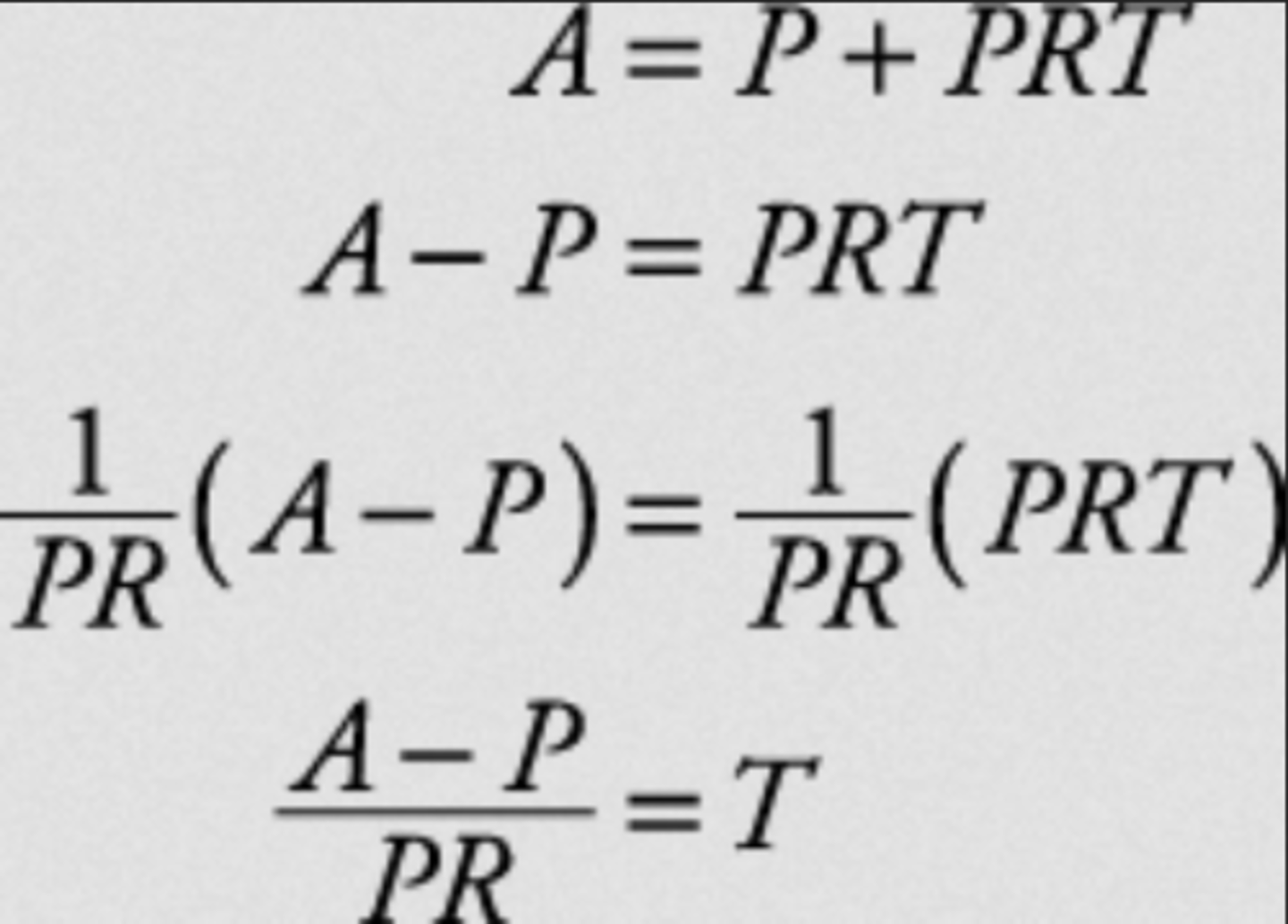
When do you flip an inequality symbol?

Anytime you multiply or divide by a negative number.

Explain each step in solving an equation.

You may have to list the steps you performed explaining what you did, step by step. Know how to justify your solutions.

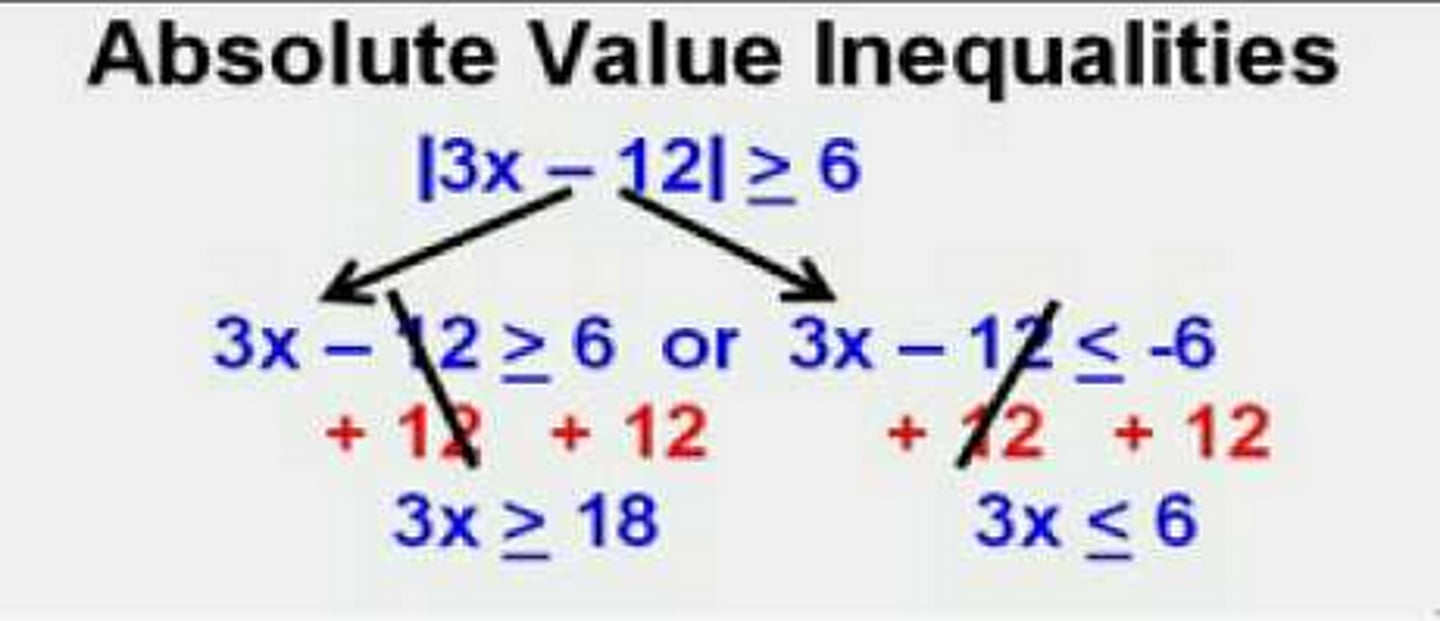
How to solve absolute value inequalities?

Once the absolute value bars are on one side of the equal sign, by itself, you work two separate problems (1) Looks exactly the same as the original equation without the absolute value symbols. (2) Is the same on one side, but flip the inequality symbol and make the number negative.

Absolute value of a negative number. IxI = -3

NO SOLUTION

Factoring with 2 terms

Factor out the number or variable that all the terms have in common.

Factoring with 3 terms

ax^2 + bx + c = 0, where a=1

(x )(x )=0 Find the two numbers that multiply to get you c, AND they add/sub to get you b. If asked to SOLVE by factoring, then set each factor equal to zero and solve.

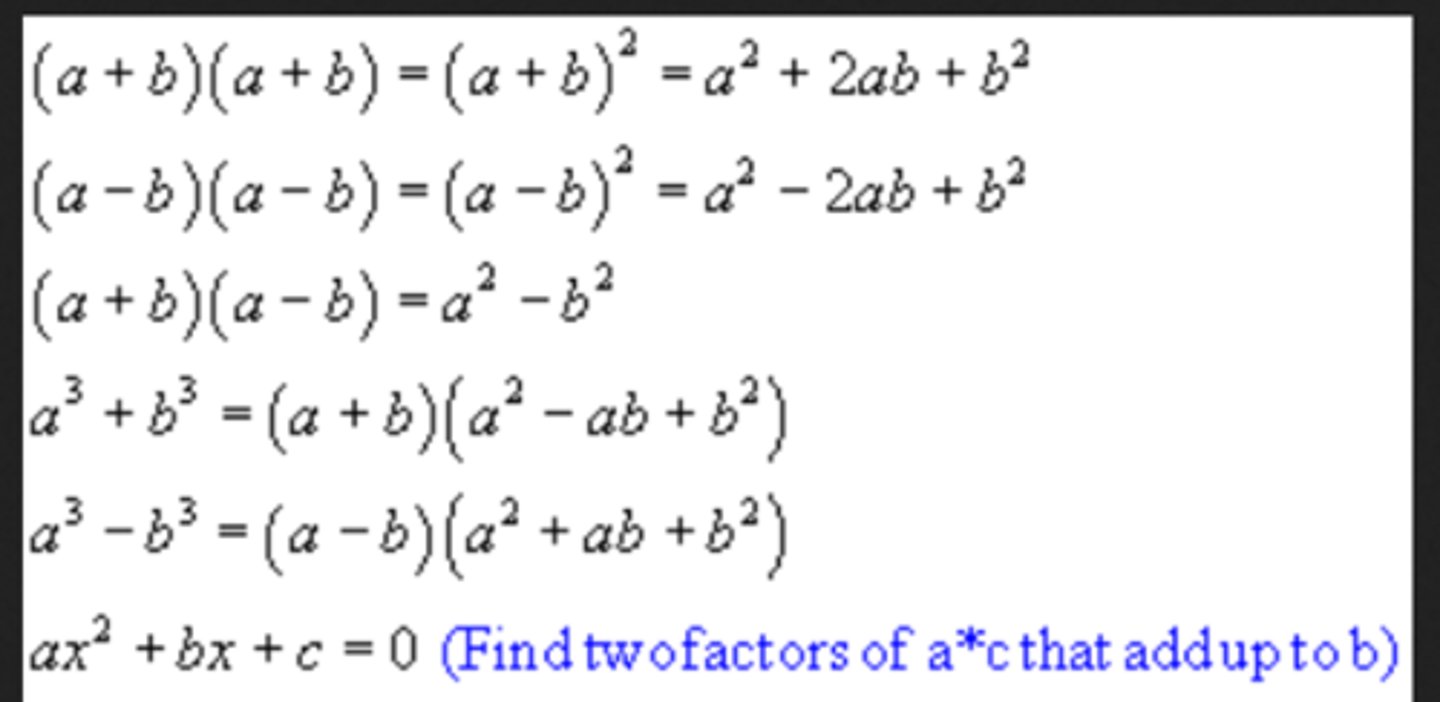
How to use the Discriminant when solving the Quadratic Formula?

If the discriminant is positive, you will have 2 solutions or x-intercepts. If the discriminant is zero, you will have 1 solution or x-intercept. If the discriminant is negative, you will have No Solution (or really a complex solution (imaginary) in the form (a + bi)

Factoring with 4 terms

Solve by grouping. Group two sets and then factor those two groups.

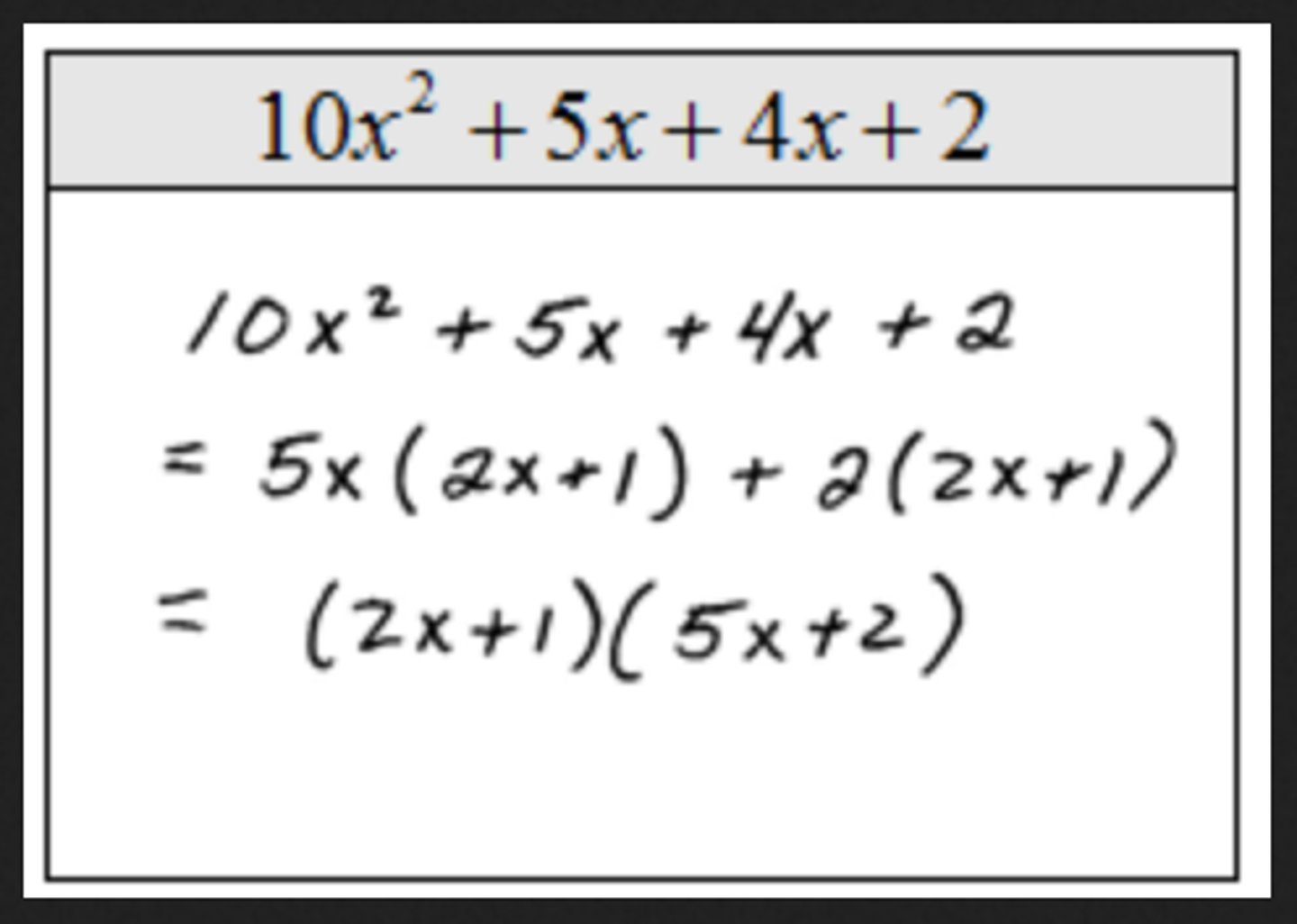
If y=f(x) and y=g(x), then.....

f(x) = g(x) meaning you can set the two equations equal to each other in order to solve for the variable. Then to find y you plug the variable back into one of the original equations and solve.

Absolute Value when solving order of operations problems.

Work any math that you need to within the absolute value bars. Then always give the positive of that number as the answer.

SUBSTITUTION

If you know what one variable equals, like y=35-10x, then you can plug that value in for y in the second equation,

4x - 7y = -23 becomes

4x -7(35-10x)=-23. Distribute and solve for x. Then you can plug back in to one of the original equations to solve for y.

ELIMINATION

You have to get one of the variables to eliminate by getting them to be the same number just one positive and one negative, so they zero out.

Sometimes in order to do this you have to multiply one or both of the equations by a number. Then add straight down and continue to solve.

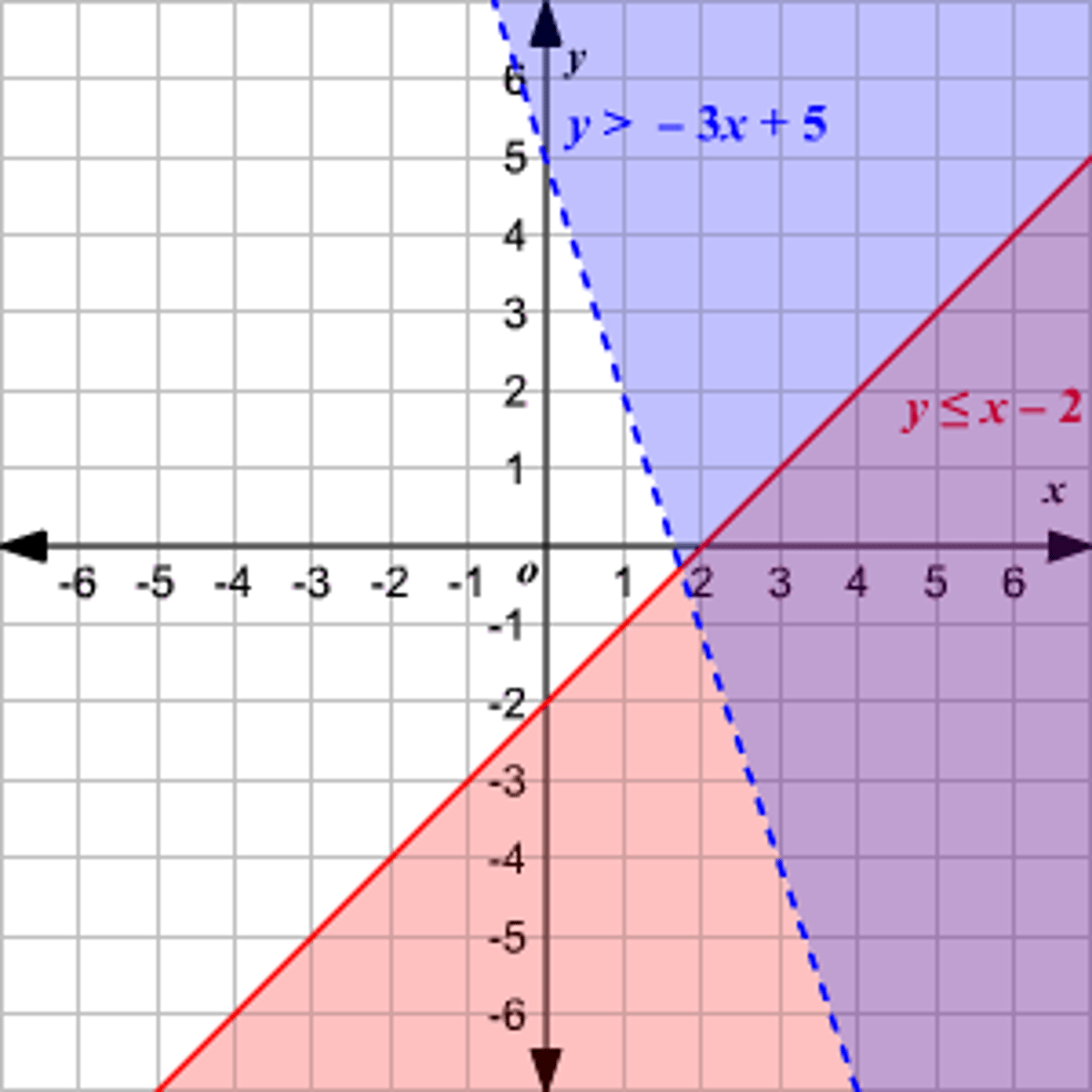
The solution to a system of linear inequalities

The intersection of the two half-planes.

Interpret parts of an expression

Examples such as: C= 250 + 35m, Where C is the cost for renting a car. They pay $250 plus $35 for every extra mile they drive. You have to interpret what the numbers and variables mean in the form of a word problem.

Use the structure of an expression to identify ways to rewrite it.

Example: See x^4 - y^4 as (x^2)^2 - (y^2)^2, thus recognizing it as the difference of two squares that can be factored as (x^2-y^2)(x^2+y^2).

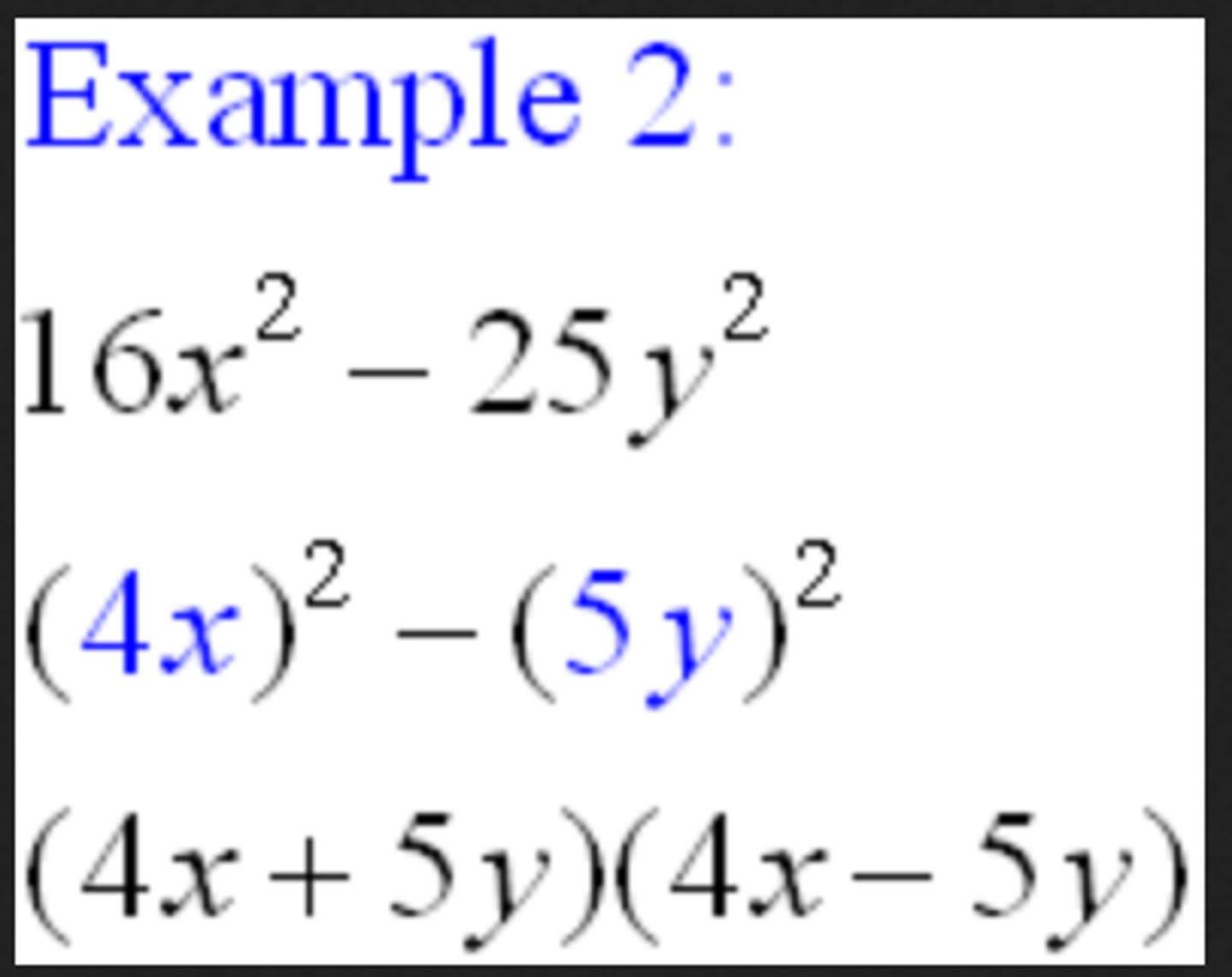
Percents

15% can also be written as 0.15, or as 15/100 which then must be reduced to 3/20.

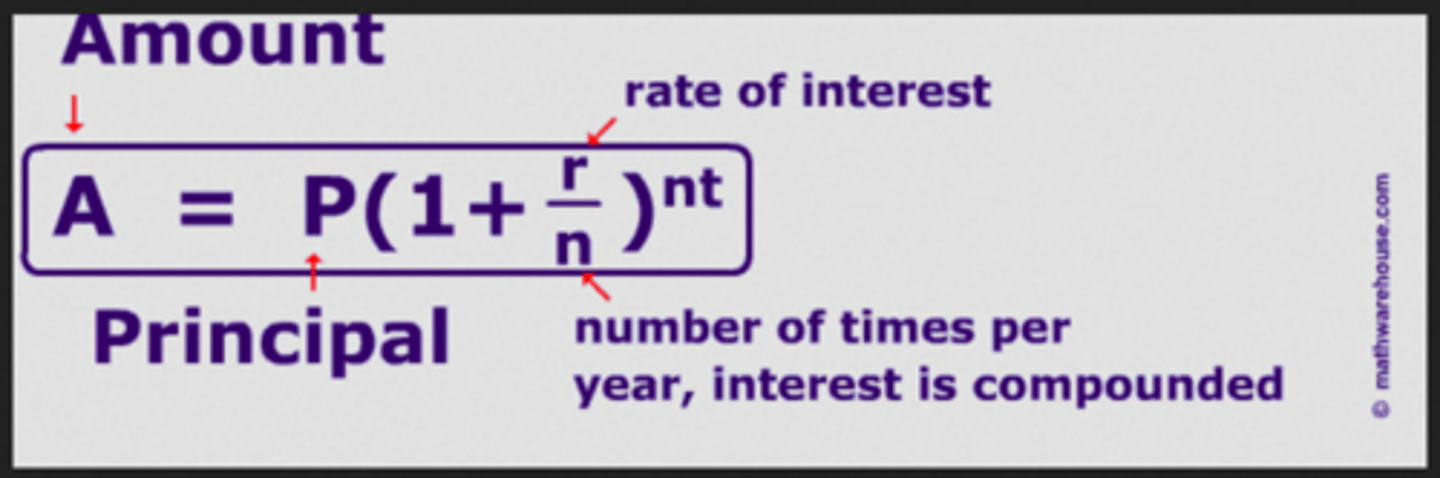
Compound Interest Formula

A=(P+r/n)^nt

Common n values are 12=monthly, 4=quarterly, 2=semiannually, 1=annually.

t is the time in years.

Simple Interest Formula

You can solve for any of the variables when given the other 3. The rate is the percentage rate usually written as a decimal. EX. 13%= 0.13

Sales Tax

Is added on to the cost of the item. To find the amount to add, multiply the cost of the item by the percent of tax.

y= and f(x)=

These are the same. They can be interchanged with one another. f(x) simply lets you know the equation is a function. Can also be written with other variables like g(x), p(x), etc.

Discounts

Are subtracted from the cost of the item. To find the amount to subtract, multiply the cost by the item times the percent being discounted.

How to solve when written in function notation.

Ex: f(x) = 3x + 4, solve for f(-2). All you do is replace the x with a (-2) and solve. 3(-2) +4 = -2

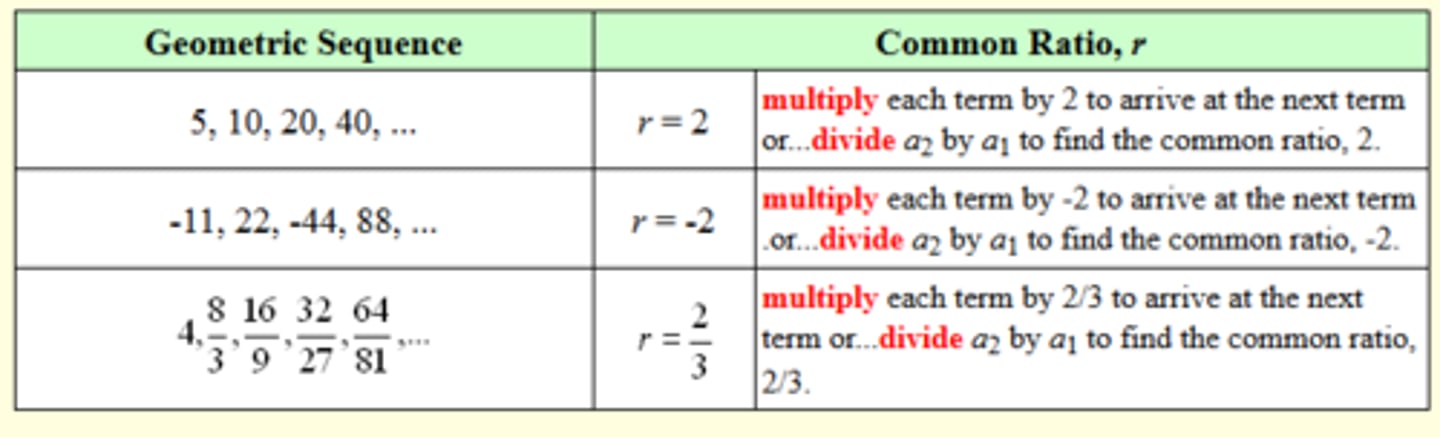
Geometric Sequences

There is a pattern in which you multiply or divide by a common number.

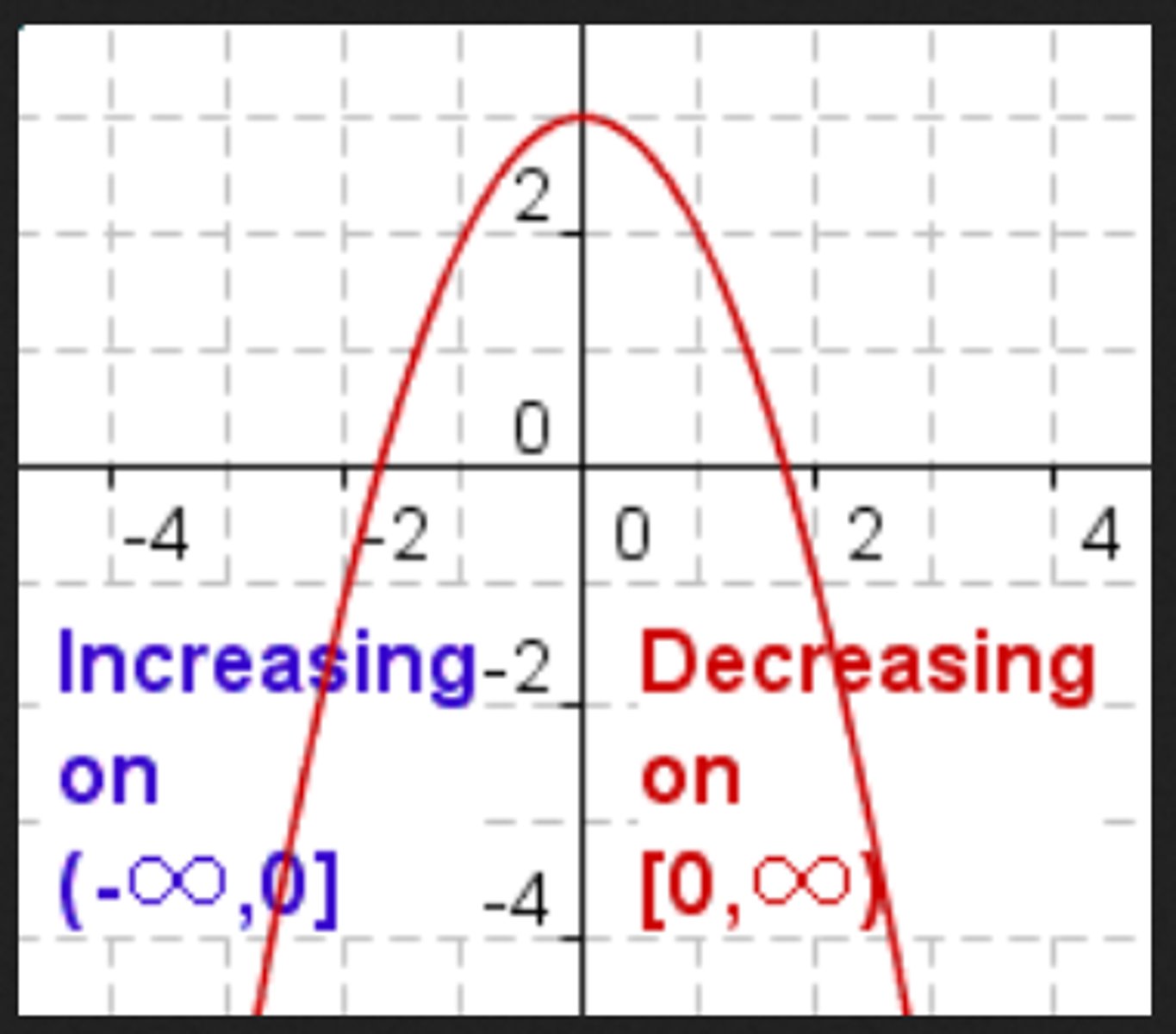
How to tell when a function is increasing or decreasing?

Always read a graph from left to right, just like the words on a page. If it goes up, it is increasing. If it goes down, it is decreasing.

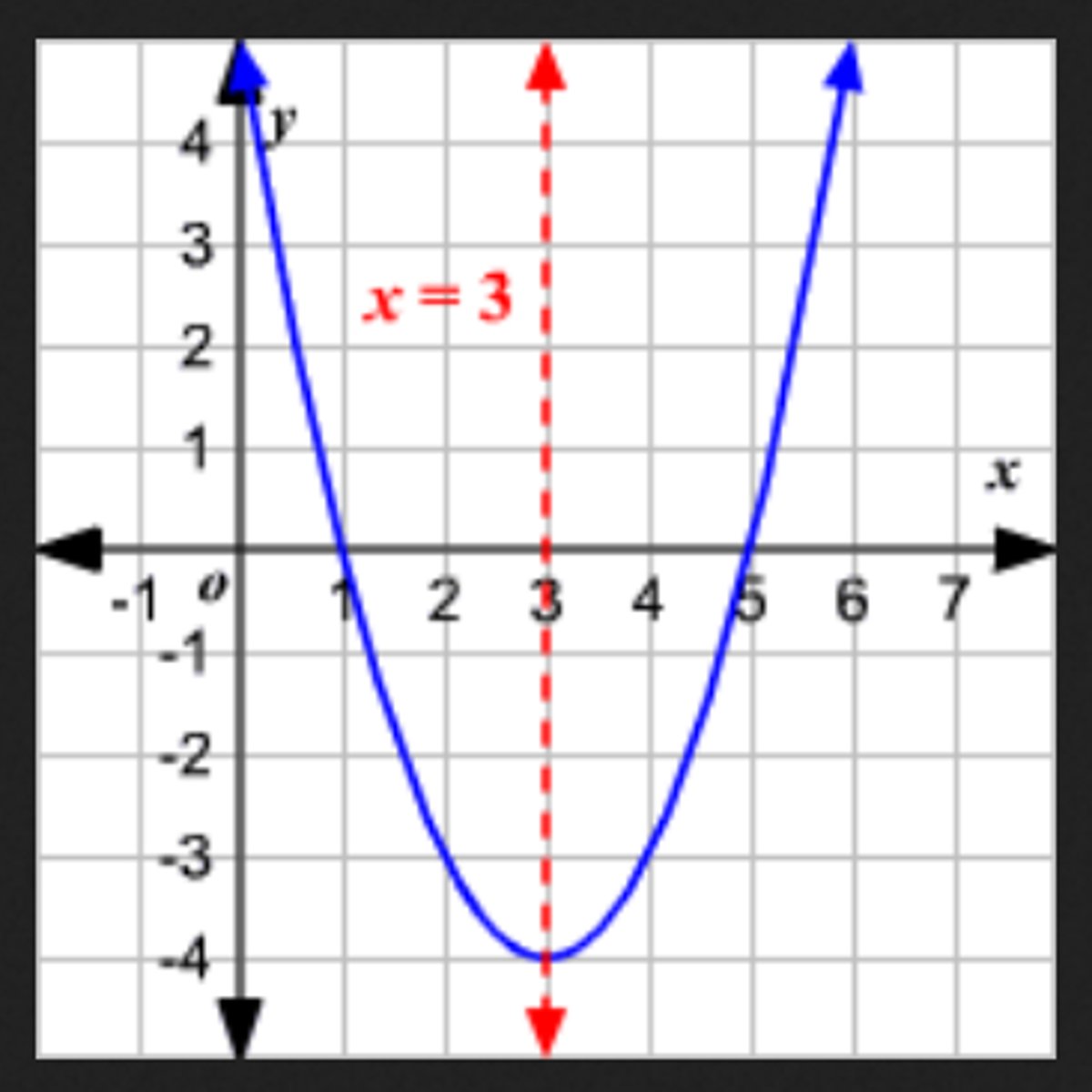
Axis of Symmetry

The equations x=0 is the axis of symmetry for a parabola in standard form.

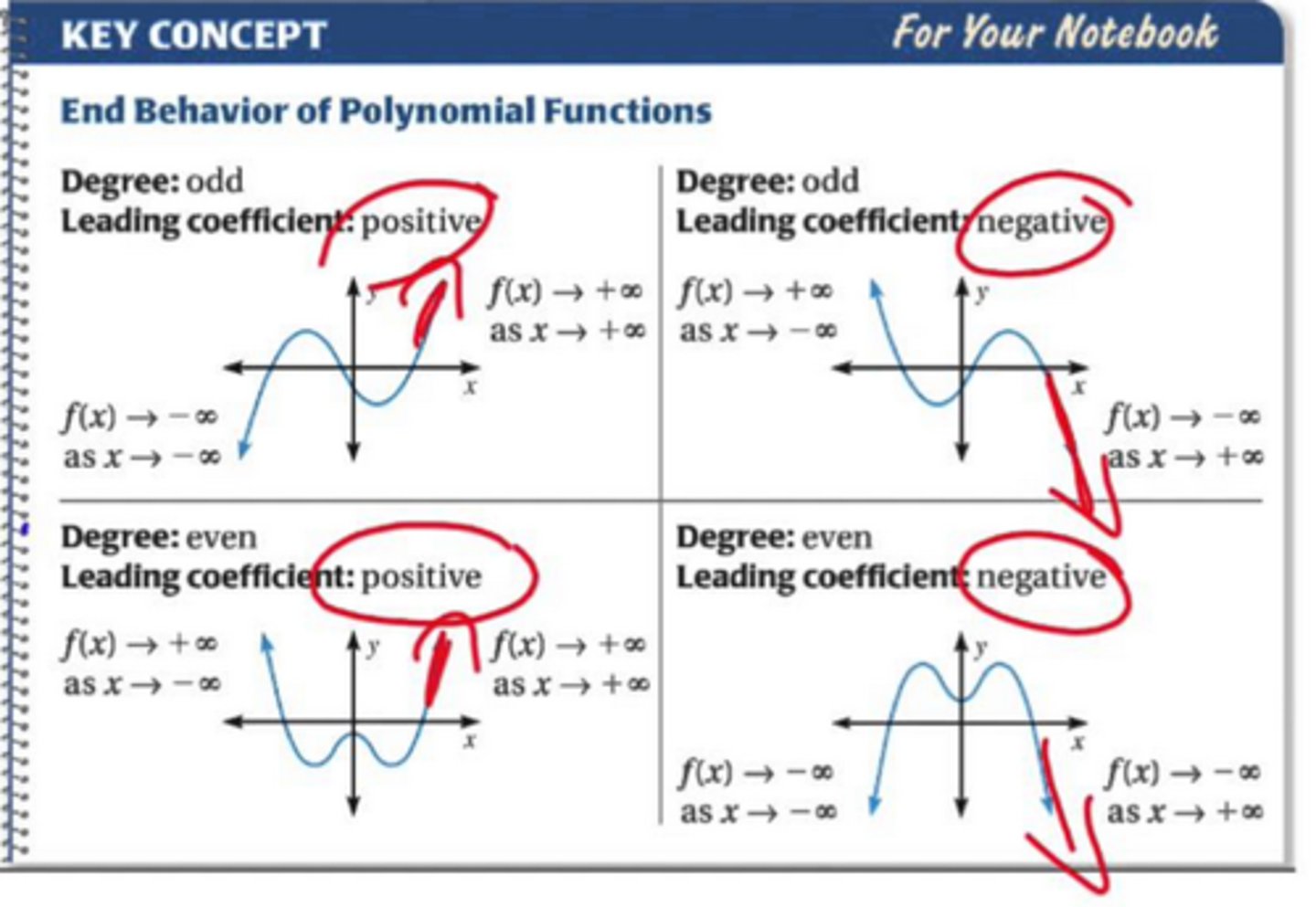
End Behavior

Describes what is happening to the graph overall as the x-values change. As the x-values decrease, does the graph seem to go up or down? As the x-vales increase, does the graph seem to increase or decrease? This represents the end behavior as being positive or negative.

Calculate and interpret the average rate of change (symbolically or from a table)

How fast is it changing? Sometimes you find out how much each one changes, then take their average.

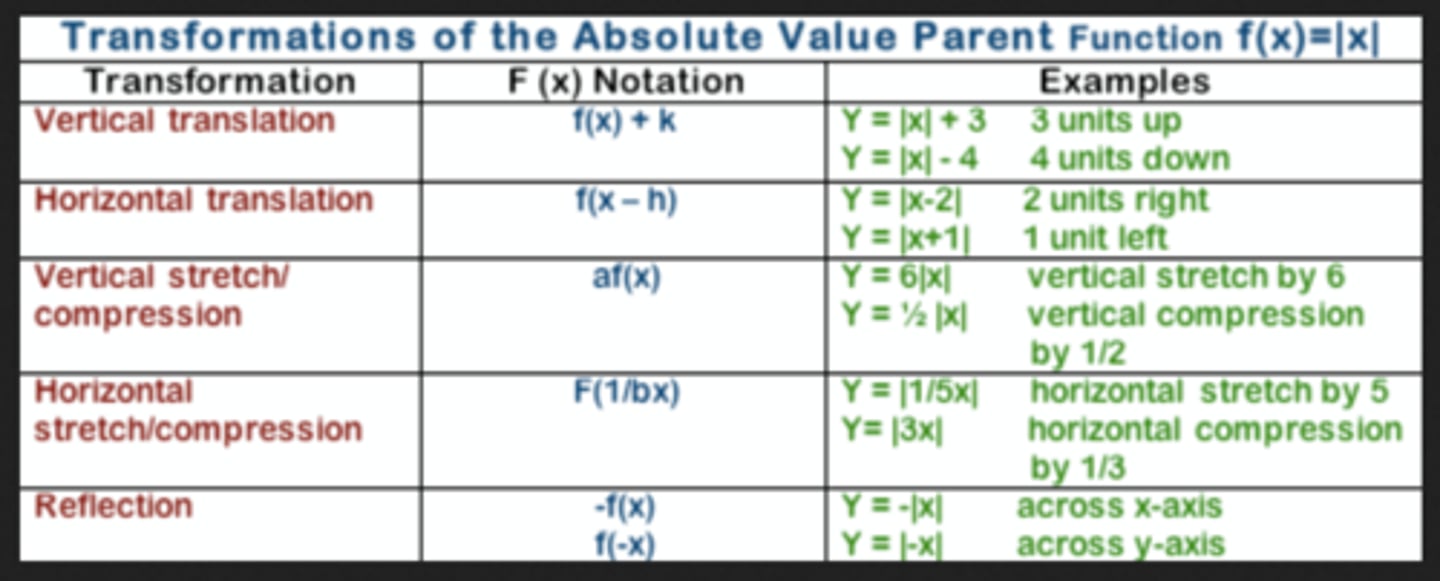
Identify the effects of k on the graph y=f(x)

y=f(x) + k moves the graph up k units or down k units.

y=f(x+k) moves the graph right if k is negative OR left if k is positive. Remember this is opposite of what's on the number line.

y=k f(x) vertical stretch if k is bigger than 1 and a vertical compression if k is less than 1.