k-means
0.0(0)
0.0(0)
Card Sorting
1/27
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
28 Terms
1
New cards
Minimizing WCSS or dissimilarity of a clustering structure is equivalent to
maximizing the inter-cluster dissimilarity
2
New cards
TSS
does not depend on the clustering structure, and is thus a constant

3
New cards
BCSS
accounts for inter-cluster dissimilarity
4
New cards
WCSS
dissimilarity

5
New cards
WCSS+BCSS = a constant, so
minimizing WCSS is equivalent to maximizing BCSS
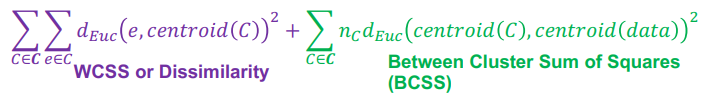
6
New cards
k-means
* Iterative greedy descent algorithm that finds a sub-optimal solution to (see image)
* K-means iteratively alternates between the following two steps:
* assignment step
* refitting step
* K-means iteratively alternates between the following two steps:
* assignment step
* refitting step
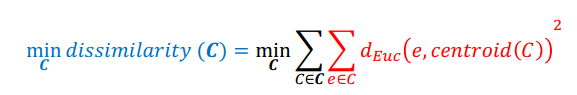
7
New cards
k-means assignment step
* For given set of K cluster centroids, K-means assigns each example to the cluster with closest centroid
* fix centroids and optimize cluster assignments (optimizes the red highlighted part)
* fix centroids and optimize cluster assignments (optimizes the red highlighted part)
8
New cards
k-means refitting step
Re-evaluate and update the cluster centroids, i.e., for fixed cluster assignment, optimize the centroids
9
New cards
K-Means algorithm input
Number K of clusters and N examples x^(1), … , x^(N)
10
New cards
K-Means Algorithm
1. Select K examples as centroids 𝑐(1) , ... , 𝑐(k)
2. Repeat 3 and 4 until cluster centroids do not change:
3. (assignment step) Form K clusters by assigning each observation to its closest cluster centroid
4. (refitting step) Compute the centroid of the obtained K clusters

11
New cards
space complexity of k-means
of the order 𝑂((𝑁 + 𝐾)𝑚), where m is the number of feature attributes
12
New cards
Space requirement for K-means is modest because
only data observations and centroids are stored
13
New cards
time complexity of k-means
𝑂(𝐼 ∗ 𝐾 ∗ 𝑁 ∗ 𝑚) where I is the number of iterations required for convergence
14
New cards
time complexity of K-means is
linear in N
15
New cards
At each iteration, the assignment and refitting steps ensure that
the objective function (1) monotonically decreases
16
New cards
K-means works with
finite partitions of the data
17
New cards
the K-Means algorithm always converge (i.e., cluster assignments do not change) because
* At each iteration, the assignment and refitting steps ensure that the objective function (1) monotonically decreases
* K-means works with finite partitions of the data
* K-means works with finite partitions of the data
18
New cards
he objective function (1) is non-convex, so
K-Means algorithm may converge to a local minimum and not global minimum
19
New cards
Choosing initial cluster centroids is
crucial for K-means algorithm
20
New cards
\
Different initializations of initial cluster centroids may lead to
Different initializations of initial cluster centroids may lead to
convergence to different local optima
21
New cards
k-means is a
non-deterministic algorithm
22
New cards
Solutions to the problem of choice of initial cluster centroids
* Run multiple K-means algorithm starting from randomly chosen cluster centroids. Choose the cluster assignment that has the minimum dissimilarity
* Specialized initialization strategies: K-means++
* Specialized initialization strategies: K-means++
23
New cards
k-means++
* Choose first centroid at random.
* For each data point 𝒙, compute its distance dist(𝒙) from the nearest centroid.
* Choose a data point 𝒙 randomly with probability proportional to dist(𝒙)^2 as the next \n centroid.
* Continue until K cluster centroids are obtained.
* Use the obtained K centroids as initial centroids for the K-means algorithm
* For each data point 𝒙, compute its distance dist(𝒙) from the nearest centroid.
* Choose a data point 𝒙 randomly with probability proportional to dist(𝒙)^2 as the next \n centroid.
* Continue until K cluster centroids are obtained.
* Use the obtained K centroids as initial centroids for the K-means algorithm
24
New cards
Choice of the Number of Clusters K
* conventional approach: use prior domain knowledge
Example: data segmentation – a company determines the number of clusters \n into which its employees must be segmented
* A data-based approach for estimating the optimal number K\* of \n clusters: Elbow method
Example: data segmentation – a company determines the number of clusters \n into which its employees must be segmented
* A data-based approach for estimating the optimal number K\* of \n clusters: Elbow method
25
New cards
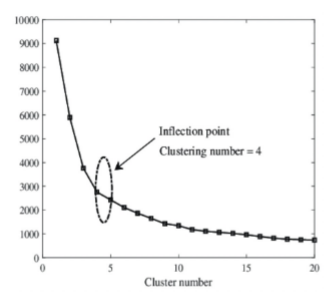
elbow method
* Apply K-means algorithm multiple times with different number of clusters.
* Evaluate the quality of the obtained clustering structure in each run of the \n algorithm using the metric 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) .
* As the number of clusters increases, 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) tends to decrease.
* Plot 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) as a function of the number K of clusters.
* Optimal K\* lies at the elbow of the plot.
* Evaluate the quality of the obtained clustering structure in each run of the \n algorithm using the metric 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) .
* As the number of clusters increases, 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) tends to decrease.
* Plot 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦(𝑪) as a function of the number K of clusters.
* Optimal K\* lies at the elbow of the plot.
26
New cards
elbow criterion
* Marginal gain in the objective may decrease at true/natural value of K
* Not always ambiguously defined.
* Not always ambiguously defined.
27
New cards
properties of k-means
* Optimizes a global objective \n function
* Squared Euclidean distance based
* Non-deterministic
* Squared Euclidean distance based
* Non-deterministic
28
New cards
challenges of k-means
* Requires as input: number of clusters and an initial choice of centroids
* Convergence to local minima implies multiple restarts
* Convergence to local minima implies multiple restarts