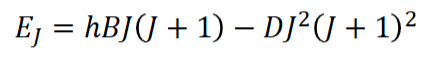rotational/microwave spectroscopy

in which regions are transitions between energy levels measured

microwave and far infrared

equation and units for wavenumber + why this is the case

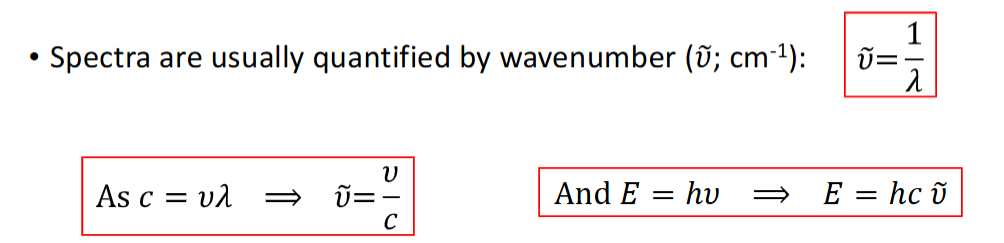
phase used for rotational spectroscopy and why?

quantities needed? how can this be achieved for the other phases?

• usually done in the gas phase

• solids inhibit rotation and too many collisions cause rapid energy transfer in liquids

• sensitive technique so only small quantities of vapour are needed. many solids/liquids can be heated to give sufficient vapour pressure to record a spectrum

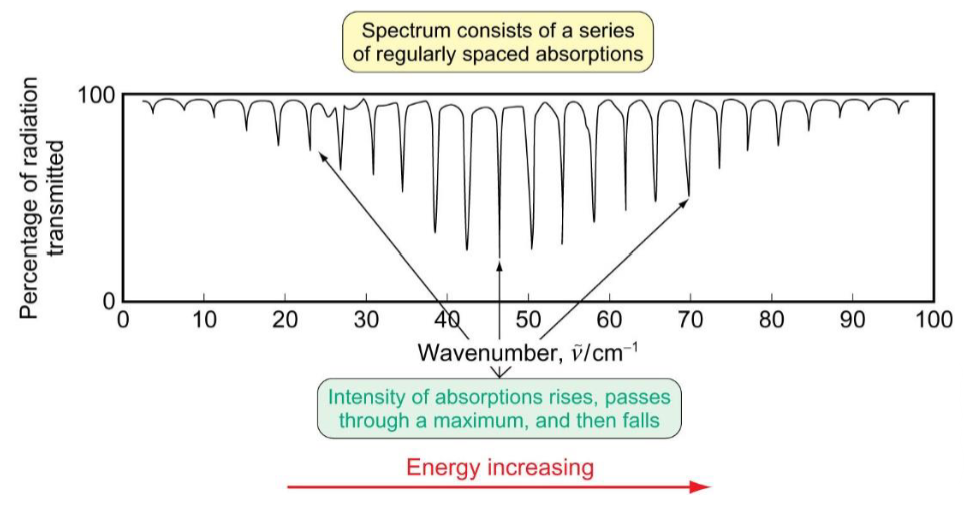
what does a rotational spectrum look like

energy?

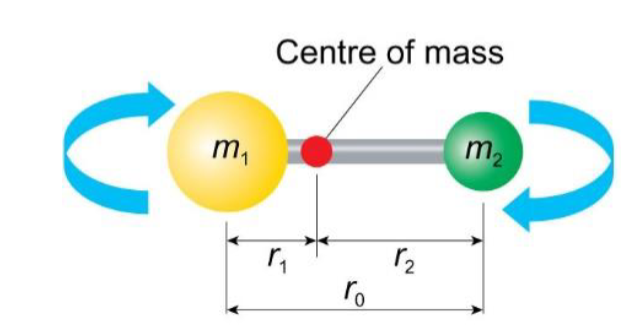
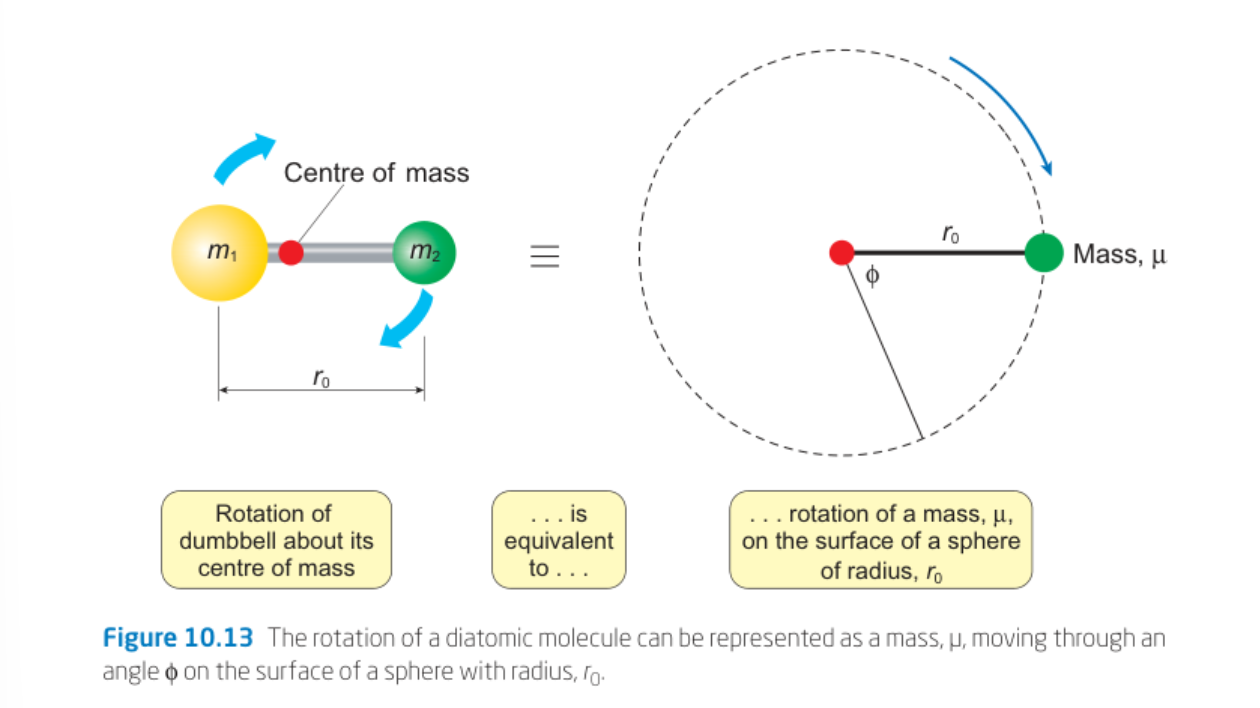
rigid rotor model

• type of molecule?

• assumption?

• diagram

diatomic molecules

model assumes the bond length is fixed between the two atoms in a diatomic molecule, ie it does not change when the molecule rotates about its centre of mass.

moment of interia

• symbol

• equation

• what it tells us

• what does a higher value mean

symbol I

tells us how easy it is to spin the diatomic molecule about its centre of mass

larger masses or longer bond lengths mean the rotor will spin more slowly for a given magnitude of push. this means the moment of inertia is larger.

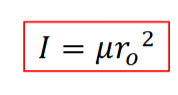
reduced mass symbol + equation

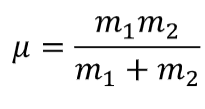
how can the rotation of a diatomic molecule be represented

quantisation of rotational energies

• symbol

• equation (not in terms of B) + what the symbols are

symbol E_J

J is the rotational quantum number and takes integer values J ≥ 0. E_J is then the energy of rotational level J

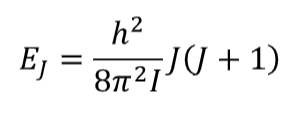
ground state for rotational energies

for J = 0, E_J = 0, so there is no non-zero ground state energy as there is for translational motion

rotational constant

• symbol

• equation

• rewrite equation for E_J as a result

• what does it depend on

symbol B

E_J = hBJ(J+1)

B is independent of J but depends on the chemistry of the molecule - each molecule has a unique value of B due to its moment of inertia I.

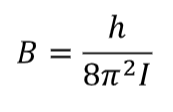
name the selection rules for rotational spectroscopy

• gross selection rule

• specific selection rule

gross selection rule

what is the case for diatomics

for a molecule to have a rotational spectrum it must have a permanent electric dipole. this is so that is has an oscillating electric dipole during rotation that can interact with the oscillating electric and magnetic fields of the electromagnetic radiation at the same frequency.

diatomics: homonuclear molecules have no permanent electric dipole and therefore no rotational spectrum eg Cl₂, H₂. heteronuclear diatomics do have a permanent electric dipole and do have a rotational spectrum, eg CO, NO.

specific selection rule

transitions can only take place between adjacent energy levels

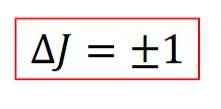
for J=0 to J=5 including energy level diagram

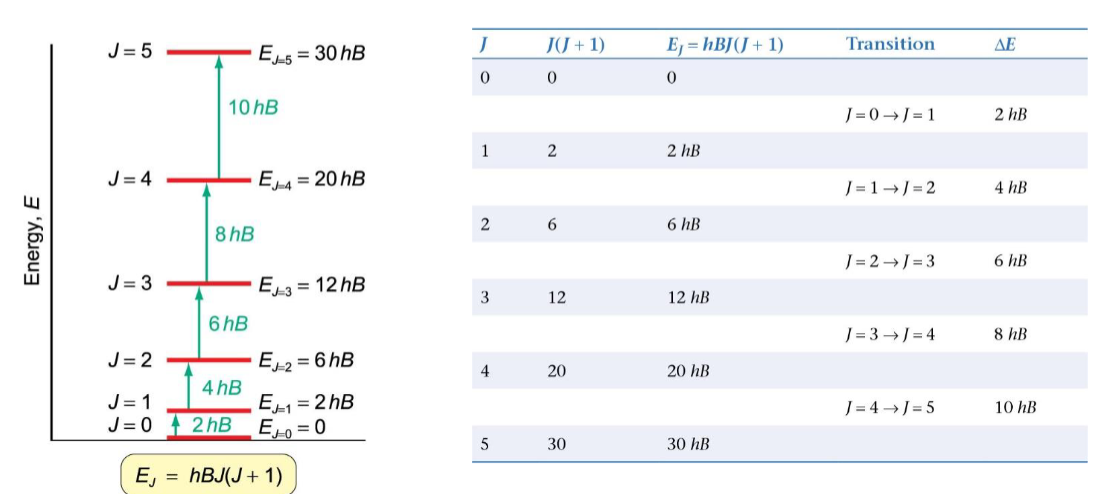
simplified rotation spectrum (don’t need to show intensity) showing ΔE and gaps between different ΔE values

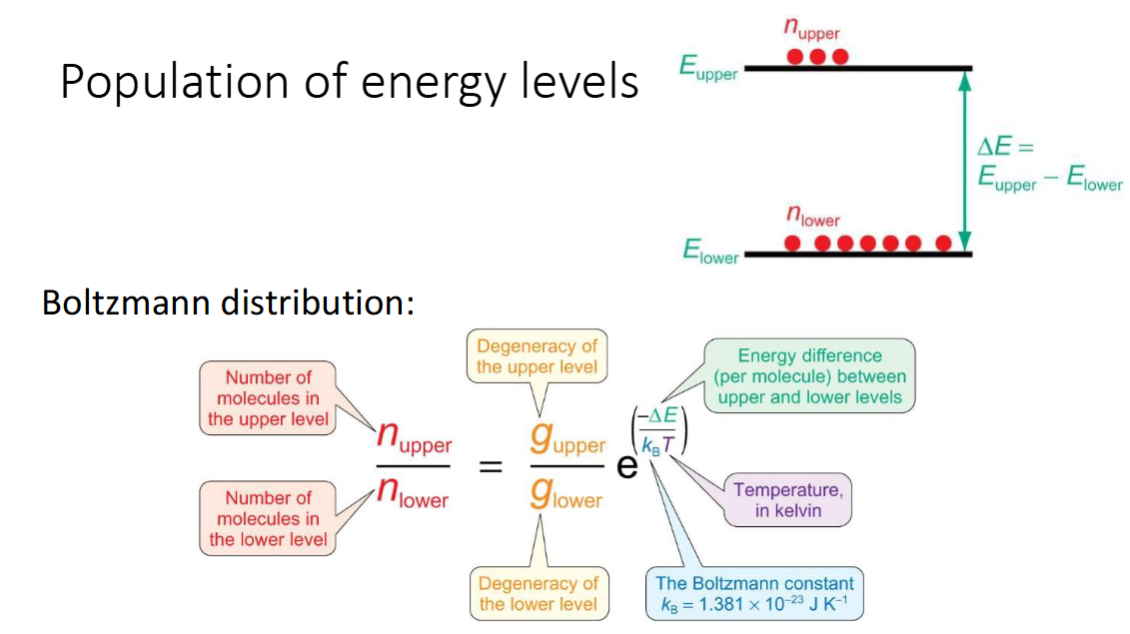
population of energy levels

• name of distribution

• equation and explain terms

• diagram to show

degeneracy of rotational energy levels

(2J+1) distinct states for the J^th energy level

eg J = 0 has a spherical symmetric wavefunction similar to an s orbital

J = 1 has three wavefunctions similar to p orbitals of the H atom

J = 2 has five wavefunctions similar to the d orbitals of the H atom

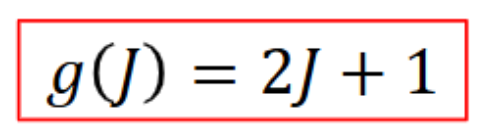
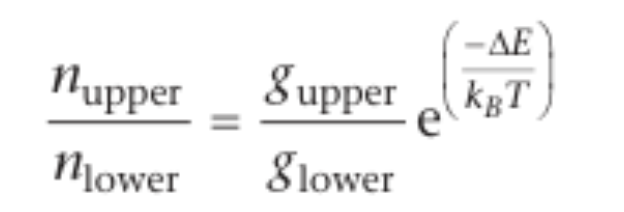
effect of degeneracies

ΔE is much less than k_BT so the population for these levels is determined largely by the ratio of the degeneracies. although the degeneracy of the level increases as J increases, the value of ΔE also increases and eventually becomes larger than k_BT - this is seen in the spectrum where the intensity increases to a maximum and then when ΔE ≥ k_BT the exponential term decreases and the peaks get lower in intensity again - the ratio of adjacent peaks is greater than 1 before the maxium and less than 1 after.

how can temperature be estimated

• ΔE can be obtained from the wavenumbers of the spectral peaks.

• peak intensities allow calculation of energy level occupancies.

• assigning peaks to specific energy levels allows calculation of degeneracies.

• temperature is then the only unknown and the equation can be used to calculate it.

how can bond lengths be measured

• ΔE = 2hB and ΔE = hv

• the separation between the spectral lines (in frequency units) is equal to 2B

• B is found (find separation and convert to Hz) and used to calculate moment of inertia I

• calculate reduced mass

• use moment of inertia and reduced mass to find bond length r₀

polyatomic molecules and simplest system

molecules with more than two atoms that have a permanent dipole give rise to rotational spectra similar in appearance to those of diatomics, however the interpretation of the data is much more complex

simplest linear example (after diatomics) is OCS

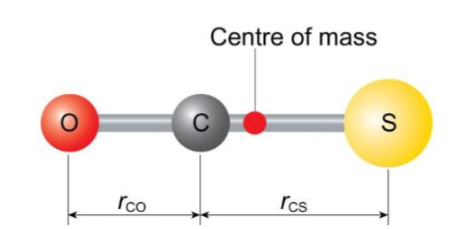
non-rigid rotors

• why this model?

• what happens as E_J increases

• equation accounting for this?

• assuming the bonds are rigid and of fixed length is not always valid

• as rotational energy increases, the molecule spins faster and the length can increase - centrifugal distortion

• this is accounted for by an extra term in the energy of rotation - D is the centrifugal distortion constant

• as rotational energy increases, the gaps between the energy levels get smaller