Esercizi statistica

30

33

si utilizza t tabulato

35

38

41

44

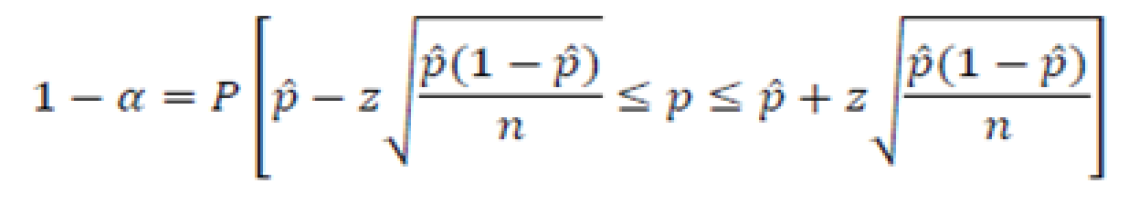
47

49

53

55

58

g.l. = n-1

60

63

g.l. di t si considerano TUTTI I VALORI: n1 + n2 - 2

65

67

69

72

74

76

79

valore tabulato f=n-1

valore tabulato t=nA+nB-2

82

85

89

sono campioni APPAIATI

calcolare D

91

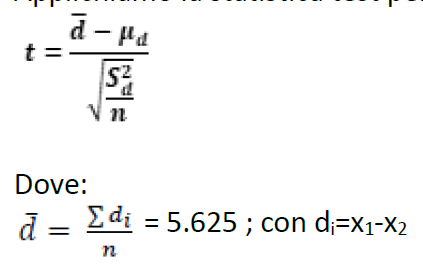
93

H1: u_d diverso da 0 quando si conforntano 2 trattamenti

96

98

100

102

106

108

110

112

test F= S²_(max) / S²_(min)

g.l. di t = (n1 - 1) + (n2 - 1)

116

120

125

127

129

131

g.l. di X²= n. gruppi - 1

137

quando ci sono più di 5 osservazioni nei vari campioni, si ricerca il valore tabulato di X² (invece che nelle tabelle di kruskal wallis), con k-1 g.l. (k → numero dei gruppi)

143

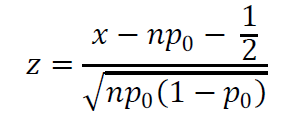
146

148

150

H0: p1=p2 (non ci sono i cappellini)

nelle formula il numeratore é: (^p1 - ^p2) - (p1 - p2)

153

distribuzione binomiale

155

157

test del X² da fare su excel

161

t tabulato: g.l.=n-2

163

t tab → g.l. k-2

165

H0: p=0 significa che non c’è correlazione

r è una stima campionaria del coefficiente di correlazione della popolazione p

si calcola r e affinchè sia valido è necessario il valore di

t=r *rad ((n-2) / (1-r²))

e t tabulato con g.l.= n-2

168

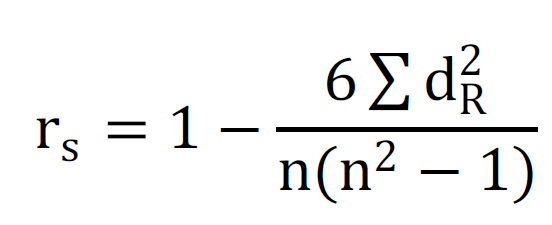
170

172

coefficiente di spearman

da confrontare con valore tabulato (intervalo)

174

ESERCIZI SBAGLIATO

è necessario applicare il metodo di confronto tra due medie di campioni appaiati e non il test per la correlazione

178

180

TABELLE DI CONTINGENZA

182

184

186

Correzione di Yates per valori inferiori a 5 o n<100;

X²=[n ( | ad - bc | - n/2 )² ] / [ (a+b) * (a+c) * (b+c) * (b+d) ]

190

X²=Σ((O_ij - E_ij)² / E_ij)

X²_tab → g.l. (i-1)*(j-1)

194

X² → g.l. (i-1)*(j-1)

199

201

203

R²= devianza di regr/ devianza totale

se R² vicino a 1, modello si adatta bene ai dati;

se R² vicino a 0, modello si adatta poco ai dati

205

207

213

219

224

228

t tabulato per alfa 1/2

232

1. si applica il confronto tra due proporzioni con metodo semiparametrico

   x²= n(ad-bc)² / (a+b)(a+c)(b+c)(b+d)

2. si deve verificare che OR si stat. significativo mediante:

   z=lnOR / ES(lnOR)

   ES(lnOR)=rad (1/a+1/b+1/c+1/d)

3. intervallo di confidenza:

   lnOR - z*ES(lnOR) < lnOR < lnOR + z*ES(lnOR)

234

z=1,96

238

Bayes → teorema della probabilità a posteriori

P(M|T+) → probabilità che M si verifichi SE si è verificato T+

P(M|T+) = P(M e T+)/P(T+)

• P(M e T+) = P(T+|M) * P(M)

• P(T+) = P [(M e T+) o (S e T+)] = P [ (T+|M) (M) + (T+|S)*(S)]

240

242

244

246