Quantitative Economics and Econometrics

autocorrelation

serial correlation of the same variable across two time periods

e.g. Bob is selected to participate in the survey where he reports his mood every week. The response in week 1 may be systematically correlated to the response in week 2.

unbiased estimator

Expectation of the estimator = true value of the estimator

Variance (general formula)

E(x²) - [E(x)]²

Panel data

Data that spans multiple time periods

Repeated cross-section? Is there autocorrelation?

In each time period, a new sample is selected. This means that across time periods and within time period, there is independence.

NO there is no autocorrelation.

tobit - when to use

there exist corner solutions, or censoring

when will truncation (or nonresponse) lead to OLS be unbiased/consistent

if the selection criteria is wholly independent of u

on the other hand, if the selection criteria depends on y (e.g. s=1 iff y>c, then s is wholly dependent on u)

first-differenced equation

taking two cross sections in two time periods, then subtracting to get a “change in” OLS eqn

distributed lag model

when there are lagged indep variables included in the regression

e.g. trash2025 = b0+ b1*govbudget2023 + b2*govbudget2022

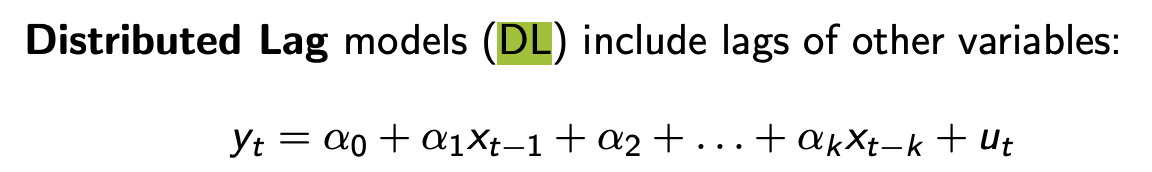
time dummies in first-difference eqns

1. why do we need them?

2. how do we interpret the coeff on the time dummy

1. for removing the time-invariant, fixed effects (a)

2. since it would be 1 for the year and -1 for the year after, it measures the effect of entering/exiting that year on y

chow test

1. what is it for

2. how do we do it

3. when is DiD or First Differences better?

write the formula

1. for comparing before and after a structural change

2. same as in F-test. compute f-statistic. But make sure the regression has dummy variables interacting on regressors BEFORE and then AFTER the break

3. DiD is better for a TREATMENT to determine causality. First differences is better when you know there are fixed effects influencing individuals/cities in diff ways

formula: let SSR1+SSR2=SSR_UR then it is the same as the F statistic formula.

SSR_R - (SSR₁ + SSR₂) / q

———

(SSR₁+SSR₂) / df

problems with first-differencing

1. key assumption that a needs to be uncorrelated with all x

2. sometimes variables do not vary much across two periods (or even more! e.g. educ)

how to deal with OVB (5 possibilities)

1. include it as a regressor

2. include more controls s.t. conditional exogeneity holds

3. use panel data, fixed effects / first-differencing, so every individual is observed multiple times (this assumes OVB doesnt vary over time)

4. IVs

5. run a randomised controlled experiment

1. what is the OLS variance

2. how is the IV variance different

3. compare sizes

1. sigma² / SSTx

2. there is also a R²(x,z) term in the denominator

3. IV variance is larger

how to know if we shd use OLS or TSLS

Hausman Test

CEV assumption

ALL regressors (including the TRUE REGRESSOR) is independent of the measurement error

bias vs consistency vs efficiency

bias = tends to produce the wrong outcome

consistency = tends to produce the same outcome (low var)

efficiency = doesn’t need a large sample size to produce a given outcome

what does logit/probit replace? why is it better?

replaces LPM

better bcos only returns fitted values between 0 and 1

what is the beta in a logit/probit (interpret)

the estimated beta in a logit/probit model is the value which maximises the log-likelihoods across all observations

How do we correct for sample selection bias

Heckman Correction

How do we perform Heckman Correction

1. Write the equation. s=1[gamma*z + v] is the selection criteria

2. Perform a probit and we are interested in the Inverse Mills Ratio lambda(gamma*z) for each observation

3. End goal: regress y on x and Lambda(Gamma*z)

What does Tobit rely on? (assumptions))

Homoskedasticity of error terms is a MUST

Error terms MUST also be normally distributed

Is it a problem to truncate x or truncate y?

Truncate y, because this leads to systematic bias in the sample

Truncation vs censoring?

Truncation is when values above/below a certain y are completely tossed away from a sample. They are out of the dataset.

Censoring is ALL individuals are sampled, they are in the dataset, but then the dependent variable is restricted to a certain range (e.g. top-coding, where salary “500,000 gbp and more” is a selection)

Truncation - use MLE truncreg (OR Heckit if truncation is from an unobserved process, like self-selection bias e.g. unemployed people are excluded from the sample)

Censoring - use Tobit

What happens (to the regression, and so to the coefficients) when you use OLS to erroneously predict a top-coded regression sample?

Since values above a certain y are censored-off, then the top-coded-out responses artificially ‘flatten’ the OLS regression

OLS produces coefficients way way below what is the true value (in fact, it tends toward zero)

Incidental truncation (sample selection bias), definition?

When you toss away samples that don’t meet a certain selection criteria (e.g. s=1[y>50]) and the selection criteria is not random

However, if the selection criteria is based on x and not y, OLS remains consistent and unbiased. E.g. if you use IQ to predict wage. But you restrict the IQ to be x>100 then OLS is still valid, but the interpretation is just slightly different in that you are estimating the effects for the population of which IQ>100

Why is it only a problem if we truncate y?

Truncating x does not give any issues, unbiasedness and consistency still hold.

But doing so for y is problematic because y and u are correlated. Hence, by truncating y, the sample selection is correlated with u (MLR 4 violated)

Steps to perform Hausman Test?

H0: cov(x1,u) = 0 (exogeneity) → use OLS

Ha: cov(x1,u) =/= 0 (endogeneity) → use TSLS

1. Regress x on z to obtain fitted values of x (I.e. run the first stage of TSLS)

2. For each observation, subtract x-hat from x, to yield v-hat

3. Regress y on x (original values) and v-hat

4. T-test to check significance of coefficient on v-hat

Derive the OLS (SLR) beta-hat from the definition.

check tablet notes for answer derivation steps

Derive the OLS (MLR) beta-hat step by step using the partialling-out method.

1. Regress xi1 on xi2, with ri1 being the error term and alphas as coefficients

2. Regress y on ri1 (y = B0 + B1ri1 + v)

3. Rewrite the OLS SLR beta-hat.

What are the ways we can test for multiple exclusion restriction in MLE? And why do we want to do it?

Compare this with the OLS case. Why is there a different methodology for MLE?

1. Wald statistic (in x)

2. LM statistic (in m)

3. LR statistic (in y) - we know the form = 2

the point is to check whether adding more indep variables makes a difference, or to see whether the indep variable is affecting the dep var at all

In OLS, we do the same using the t-statistic. MLE has diff ways to find bc u is not assumed normally distributed.

weak vs strict exogeneity

weak: E(u|x) = 0

strict: E(u|X) = 0 (as in, the average of error terms must be uncorrelated across time periods)

OLS exogeneity vs TS exogeneity

(Why do we need strict exogeneity in TS?)

under cross-sections/OLS, we need just weak exogeneity because the samples are chosen from a random process

under TS, we need strong exogeneity because samples are not random.

Bidirectionality in TS? Is it ok

If y affects x too, (endogeneity), generally TS3 condition is violated - strict exogeneity does not hold true

How do we model an exponential time series

use log specification on y, linear on independent variables

spurious regression problem

when x is erroneously concluded to have a positive effect on y.

when in fact an omitted variable TIME naturally causes both x and y to increase with time.

When there exist serially correlated errors, standard OLS variances are invalid because…

They assume that the covariances of the errors across observations are zero. 

The number of lags in an AR or DL model is best chosen using…

An information criterion like BIC (Bayesian Information Criterion)

What are the appropriate ways to adjust for seasonality? (3)

1. Include month dummies

2. Use trigonometric functions as controls

3. Use an annual change transformation (1st differencing)

Why does QLR have different test statistics to T? Is it larger or smaller than T?

The QLR test statistic is the maximum out of many test statistics. It is therefore larger than T.

Random walk process - definition? What happens to the variance? And what about stationarity? What type of trend is this?

When is the only time a random walk “OLS consistent”?

When the autocorrelation term (Beta) is exactly equal to one. Variance increases linearly over time. Violates stationarity and weak dependence. This is a stochastic trend (unit root)

A random walk can be OLS consistent ONLY if the error term is stationary AND the regressor and regressand are cointegrated (cointegrated = fancy way of saying they move together. e.g. short term and long term interest rates)

Because of lack of what in TS do we need additional/new requirements compared to OLS? And what are these requirements?

Lack of random sampling

New requirements: Weak dependence, stationarity, and strict exogeneity

MA model (Check TS requirements)

Moving average model

• Satisfies both weak dependence and stationarity

• Values, especially errors from more than 2 periods ago has no effect on current y

y = beta(e_t-1) + e_t

Assumption we need to make to establish stationarity?

u is independent of the dependent variable cov(u,x_t)=0

AR(q) model assumption for weak dependence?

Beta must be less than 1.

Derive the mean and variance of a stable AR model (What must we assume? What abt the autocorrelation?)

(ASSUME STATIONARITY. As it is autoregressive, there exists autocorrelation)

By stationarity, E(y_t) = E(y_t-1). Take expectation of both sides of the model. Then E(y_t) = B₀ / (1-B₁)

---

Take variance of both sides of model. By stationarity, Var(y_t) = Var(y_t-1).

Var(y_t) = sigma²_e / 1-B₁²

Derive the mean and variance of a random walk AR? And with drift term?

With drift term:

• The mean is E(y_t) = alpha₀t + E(y₀)

• The variance is Var(y_t) = sigma_e²t

Log-likelihood function (Write down the formula) for Probit/Logit

What does the MLE try to do?

The MLE chooses beta to maximise the log-likelihood function

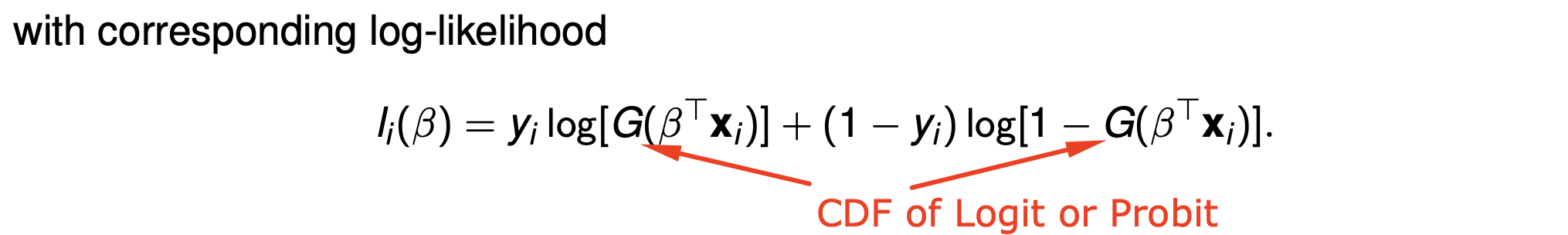
CDF of Probit

Probit uses the normal distribution.

The CDF is therefore the area underneath the PDF. PDF = 1/sqrt(2pi) * exp(-z²/2)

So take the integral of PDF evaluated from -inf to z.

CDF of Logit

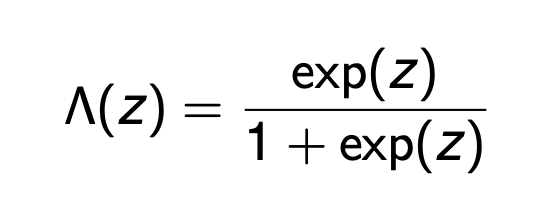
How do we test whether to include more lags in forecasting model? (1 do and 1 don’t)

In the first place, use AIC/BIC to determine the best number of lags.

If unsure, DO compute the RMSFE in the regression w/ and w/o the new lag variable. If it FALLS then yes include the lag.

DO NOT test for coefficient significance on lag (this does not necessarily tell us whether the new variable improves forecasting - pvalues are good for within-sample inference but not OOS forecasting)

forecast interval assumptions and formula

assume:

u is normally distributed

if using transformations (like log), the forecasted change is small

formula:

y-hat_T+1|T ± 1.96(RMSFE-hat)

Is it ok if coefficients are biased in forecasting

Yes because we just care whether the forecasting is correct

How do I obtain the effect of x on y if using PROBIT/LOGIT?

If x is a discrete regressor, then simply plug in values into the cdf. For example if we want to measure the effect of going from x=3 to x=4,

CDF(B0 + B1(3)) - CDF(B0 + B1(4))

If x is a continuous regressor, then we would have to find the marginal. = G’(B0 + B₁x)B₁ Take the derivative of the CDF and evaluate at x=3. In the probit case that would be the Normal PDF. In the logit case that is PDF=CDF(1-CDF)

Logit pdf

PDF = CDF(1-CDF)

Where CDF = exp(.)/(1+exp(.))

What is the key assumption to probit

We are using the normal distribution, specifically the standard normal (mean = 0, variance = 1)

We need to standardise normal distributions that are nonstandard, by dividing by sigma

Partial effect at the average (Formula?)

Average partial effect (Formula?)

PEA = pdf(B^Tx)*B_j

APE = (See image)

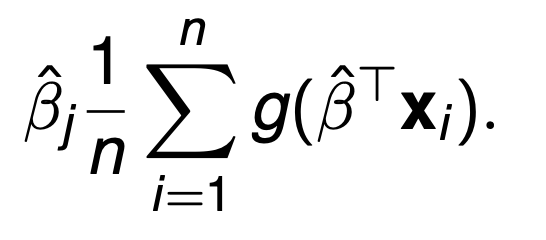
how do we know whether the data fits well for probit/logit/tobit

use Pseudo R² = 1- [ln(L_UR)/lnL_R]

Where L is the log-likelihood

Log-likelihood function (Write down the formula) for Tobit?

How is the function different if it is not ‘above’ censored but instead ‘below’ censored?

Note: The ENTIRETY of c_i - BtX should be divided by sigma (error in the slides)

If it is below censored, then the sign obviously flips, but also no need to do 1- in the first bit.

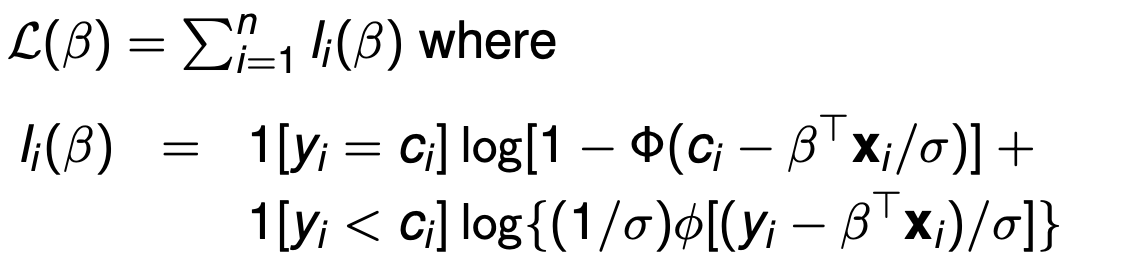
What does beta measure in Tobit?

Beta measures the effect of x_j on the observed values of y, i.e. y*

Tobit conditional partial effect (what is it? Formula?)

Conditional partial effect is E(y|x, y>0)

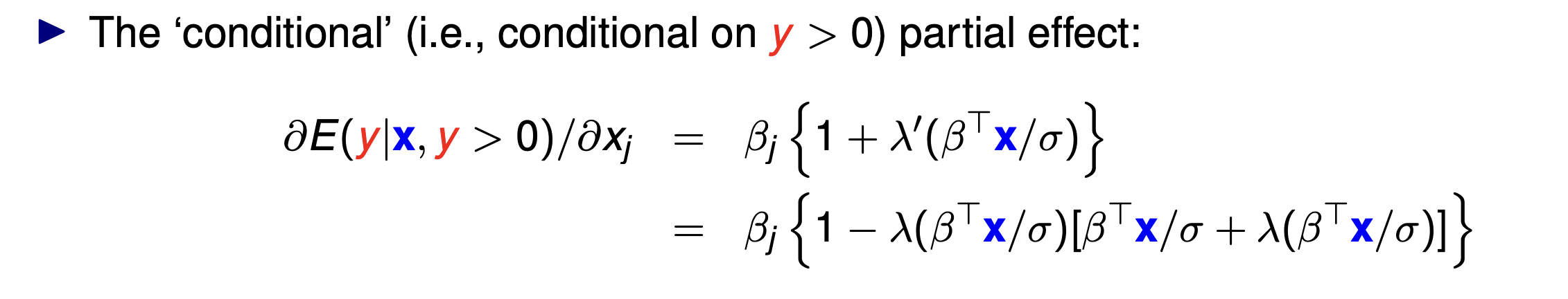
Inverse mills ratio formula

PDF/CDF

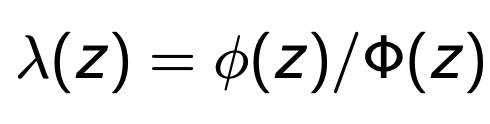
Tobit unconditional partial effect (What is it similar to? Definition? Formula?)

Unconditional partial effect is E(y|x).

The formula is similar to the probit/logit continuous PEA. Except note that we use cdf instead of pdf. and we must standardise the value.

“Unconditional” because it is NOT conditional on y being greater or less than the censor threshold c

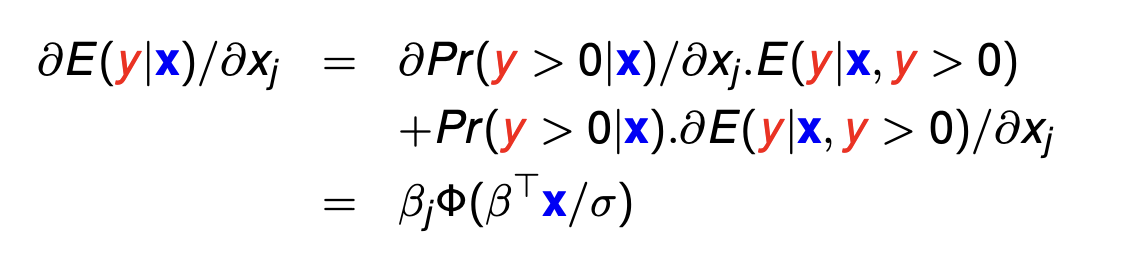
how do we know the autocorrelation of an AR model?

how do we know if an AR model displays weak dependence?

The coefficient on the lag is the sample autocorrelation

IF AR model has B<1, → weak dependence

if random walk or B>1, → no weak dependence

percentage change in time series formula

100Δln(Y_t)

= 100(ln(Y_t) - ln(Y_t-1))

this can be shown to equal 100*(change in Y_t formula)

= 100(ln(Y_t/Y_t-1))

= 100(ln(1+(Y_t - Y_t-1)/Y_t-1))

approx equal to 100(Y_t - Y_t-1)/Y_t-1)

Holds for small changes in Y_t

Autocorrelation formula

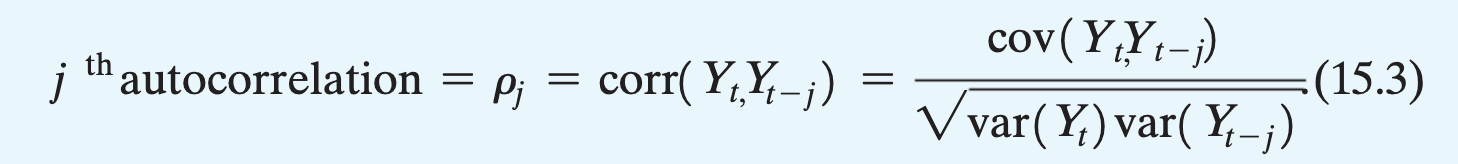
General formula for correlation

This is how the correlation coeff, r, is calculated

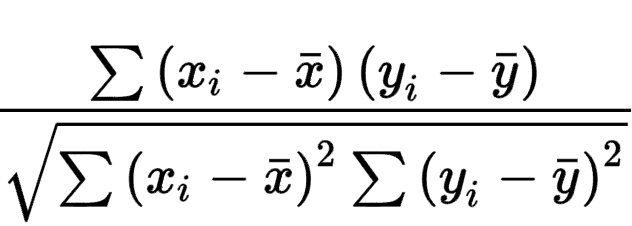
Sample autocorrelation formula

the denominator is simply var(yt) because we have assumed var(yt) and var(yt-1) are the same under stationarity.

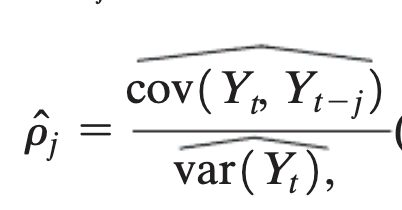
Textbook definition of stationarity

Historical relationships can be generalised to the future because the distribution of Y_t is same over time.

Formally, the joint distribution of (Y_t+1, Y_t+2, …) does not depend on t

What is the formula for forecast error? And hence the formula for MSFE? RMSFE?

Forecast error = Y_T+1 - Y-hat_T+1|T

MSFE = exp[(forecast error)²]

RMSFE = root of MSFE

How is the QLR test statistic found? Explain in detail

For every time period between [.15T, .85T] = [t1, t2],

1. Create a regression equation for each break date you would like to test (every period in the data). With a dummy variable =1 if t>break date, =0 if not.

2. yt = b0 + b1y_t-1 + a₀t + a₁t*y_t-1 + u

3. The null hypothesis is H0: alpha0 = alpha1 = 0. The alternative hypothesis is at least one of them is not equal zero. Repeat for every possible time, t.

4. Compute the joint f-statistic, and find the maximum one.

note: the QLR cannot be performed on the last 15% of data, but we can still check whether there is a structural break in the last 15% by comparing the POOS forecasts with the actual data

What are the three ways to calculate RMSFE?

Sample error method

Final prediction error method

Pseudo out-of-sample method

POOS method (Steps?) and hence write the formula for MSFE under POOS

1. Choose a number of out-of-sample observations, P (s=T-P) s will be your in-sample observations (Usually 10%/20% left of T is P)

2. Estimate regression y on s.

3. Calculate Y-hat for 1 period ahead of s, and find the forecast error.

4. Repeat for every period in P until you get many forecast errors

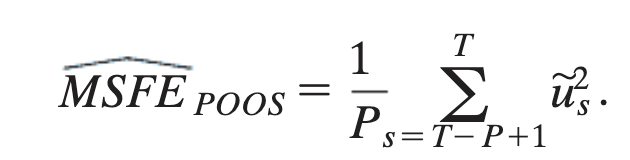
Sample error method for finding MSFE

ASSUME: Stationarity

• Write out the MSFE formula and expand for both

• We have the oracle forecast variance and estimation error

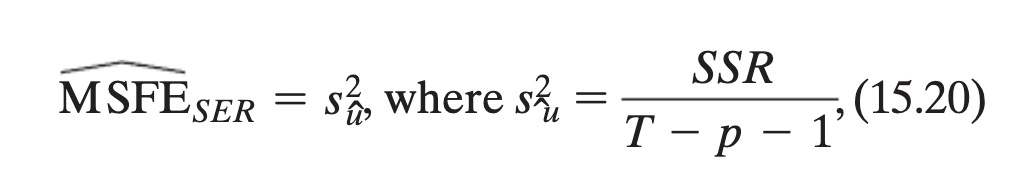
Final prediction method for finding MSFE

Assume: Stationarity, homoskedasticity of errors

T = observations

p = number of lags

deterministic vs stochastic

stationairty implies…?

deterministic: trend has a determined pattern, a clear trend. Stationary → deterministic

stochastic: trend appears to be random

Dickey-Fuller test (What is it for? How do we do it?)

It is to determine whether a AR model is stochastic or not (unit root or not)

H₀: B₁ = 1 H_A: B₁ < 1

steps:

1. let a₁ = B₁-1, regress deltaY on Y_t-1

2. calculate the Dickey-Fuller statistic a₁/SE(a₁)

3. compare to critical values

note: we DO NOT RUN A T-TEST as OLS does not work

How do we check for structural breaks?

Use the QLR test for the centre 70%. For the last 15%, the POOS observations can be used to generate a forecast. Plot this against the true values and see if they deviate.

QLR test steps:

1. Create a regression equation for each break date you would like to test (every period in the data). With a dummy variable =1 if t>break date, =0 if not.

2. yt = b0 + b1y_t-1 + a₀t + a₁t*y_t-1 + u

3. The null hypothesis is H0: alpha0 = alpha1 = 0. The alternative hypothesis is at least one of them is not equal zero. Repeat for every possible time, t.

4. Compute the joint f-statistic, and find the maximum one.

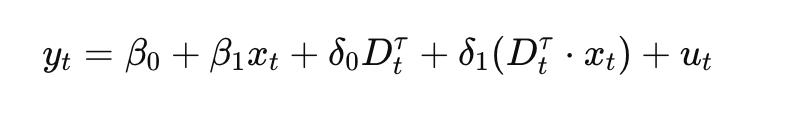
What is meant by “dynamic causal effect”

In a distributed lag model, a particular X_t will have effects that span not only for Y_t but also Y_t+1, Y_t+2, and so on…

The dynamic causal effect is the effect of X_t on all Y_t, Y_t+1, Y_t+2, …

i.e. the sequence B₁, B₂, B₃, …

Anytime a DL model includes a human element, it is likely that…

Strict exogeneity may be violated.

Because humans are forward-thinking. Changing future value of Y would likely influence a different pattern for X

Autocorrelation is a problem for the …

It does not affect…

But, autocorrelation won’t be a problem if we assume…

STANDARD ERRORS in OLS. This leads to problems for inference. That’s why we use HAC SEs.

It does not affect the accuracy/consistency/biasedness of the coefficients

If we assume homoskedastic standard errors, then autocorrelation is not a problem. BUT… this is often a terrible assumption which is why we use HAC SEs.

How do we find the MSPE (steps)

The mean-squared prediction error

• Use M-fold Cross Prediction

This is the similar process as what we did for finding MSFE.

STEPS:

1. Determine m, the number of folds. Divide your sample N by m as equal as possible.

2. Using all but subsample m=1, estimate OLS and find the MSPE-hat for m=1

3. Repeat for m=2 (Do include m=1 here) and so on, until all the m has been done

4. Calculate the eqn in the image

MSPE. What are the two ways to estimate it. Report the formula for the more ‘strict’ way to estimate it.

You can use m-fold cross prediction or use MSPE_OLS. MSPE_OLS is more strict because HOMOSKEDASTICITY IS REQUIRED.

where k is the number of regressors…

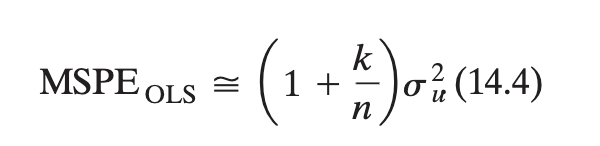
OVB bias direction intuition?

Bias direction = sign of corr w/ x * sign of effect on y

checks for internal/external validity (5)

1. OVB

2. Linear model misspecification

3. Errors-in-variables bias (measurement error)

4. Sample selection bias

5. Simultaneous causality bias

OLS estimates (b1 and b0) for binary explanatory variable

B-hat1 = ybar1 - ybar0

B-hat0 = ybar0

average treatment effect

ATE = ybar(1) - ybar(0)

However, this is not observed. This requires us knowing what would happen to EVERY individual if they somehow were both in the control and experiment

Instead, we only observe y₀ and y₁. y₀bar is not the same as ybar(0) … because it is the ybar of the observations assigned 0.

Sample variance of u formula (under OLS)

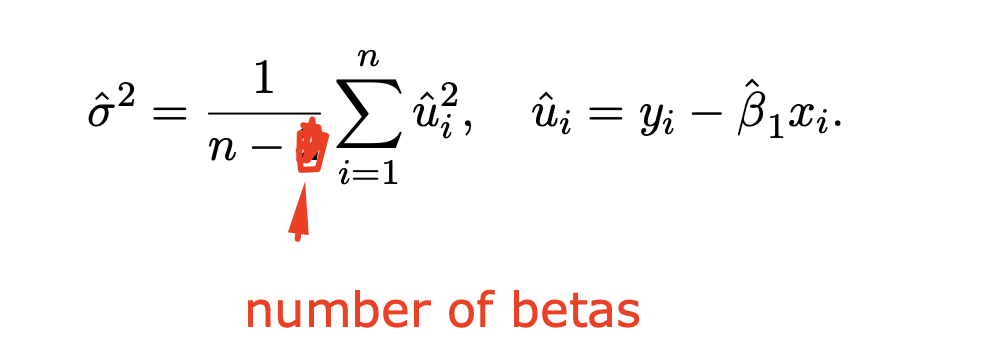
If both the regressor and regressand are in the log-form, how do we interpret the coefficient on the regressor?

e.g. log(y) = b0 + b1(logx)

A 1% increase in x is associated with a b1% increase in y.

Variance of B₁-hat for MLR

The denominator is also equiv. to sum(r_i1-hat)²

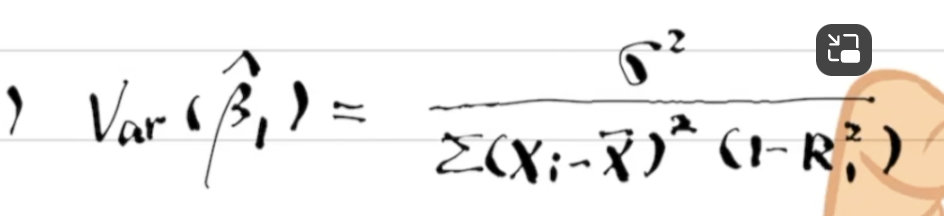
Derive the proof of OVB

SER/RMSE formula

SER means standard error for the regression.

= sqrt(SSR/n-df)

NOTE: The red highlighted should be n-df

ALSO: SSR=sum(u-hat)²

HAC / Newey West standard errors

????

F-statistic formula (there are three forms)

where q=number of restrictions (n-k-1) is the df

R² form of the formula

F = (R²_UR - R²_R)/q all divided by 1-R²_UR/df

and finally the joint significance of an unrestricted model can be tested if the R² is known. But the test must be on ALL the included variables.

F = R²/q / (1-R²)/df

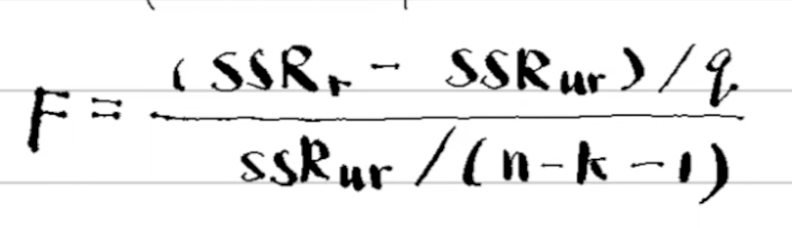
consistency formula (how do we know if b1-hat is consistent)

show that plim(b1-hat) = b1

how to prove the asymptotic normal distribution?

1. show that the estimator is unbiased

2. show that the variance of the estimator is = …

3. then the numerator of the expression is ok (by 1) and the denominator of the expression is just 2. so it converges asymptotically to the normal dist (0,1)

What is the overidentification test for?
Write the steps.

It is to check the validity of an instrument, namely, that the IVs are exogenous

REQUIRED: more instruments than endogenous variables

H₀: all IVs are exogenous

H_A: H₀ is false

1. Regress u_i-hat (from 2nd stage of TSLS) on known exogenous variables (x₂, x₃, …)

2. Look at the generated R²

3. The test statistic is nR²~X²_#endog. Reject H₀ if it has a low p value

IV Estimator (TSLS) steps

regress x on z and all other exogenous variables

regress y on x-bar and all other exogenous variables

the b1 obtained from the 2nd stage regression is the iv estimator

relevance test

for iv estimation, see if the instrument is weak or if it actually works with the endogenous variable

1. run 1st stage of TSLS (regress x on z and other exog vars)

2. test the coefficient on z using t-test