MATH REVIEWER

(Quadrilaterals, triangles, similarity and congruence)

Consecutive Exterior

Angles that are supplementary when formed by two parallel lines and a transversal.

Consecutive Interior

Angles that are supplementary when formed by two parallel lines and a transversal.

Alternating Exterior

Angles that are congruent when formed by two parallel lines and a transversal.

Alternating Interior

Angles that are congruent when formed by two parallel lines and a transversal.

Diagonals

Line segments that bisect each other in a quadrilateral, dividing each other into equal parts.

Perpendicular

Two lines that intersect to form 90-degree angles.

Quadrilateral

A polygon with four sides.

General Quadrilateral

A four-sided polygon that has no parallel sides.

Parallelogram

A quadrilateral with two pairs of parallel sides.

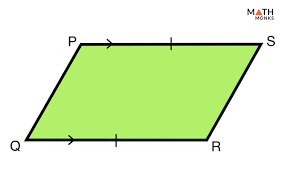
Rectangle

A quadrilateral with four right angles and opposite sides that are congruent.

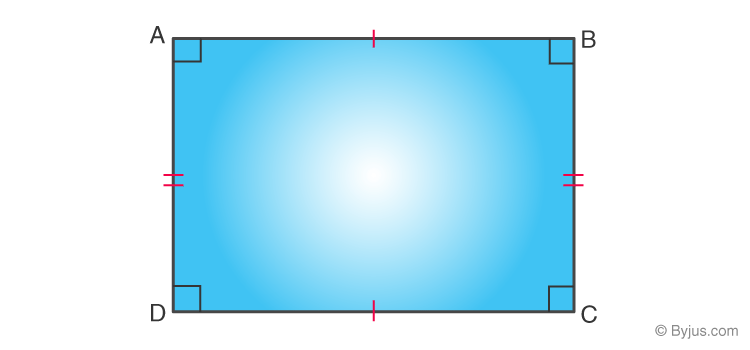
Square

A quadrilateral with four right angles and four equal sides.

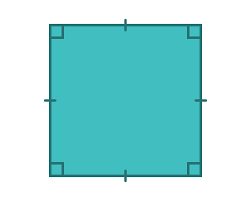
Rhombus

A parallelogram with four equal sides and opposite angles that are congruent.

Trapezoid

A quadrilateral with one pair of parallel sides.

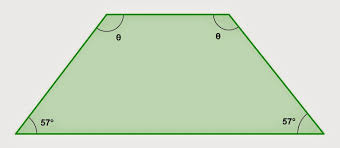
Isosceles Trapezoid

A trapezoid with one pair of parallel sides and the non-parallel sides that are congruent.

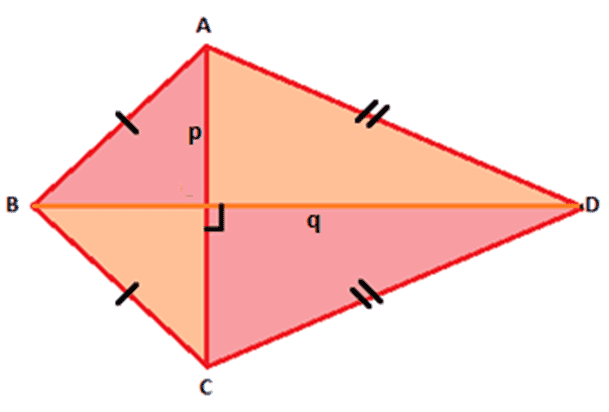
Kite

A quadrilateral with two pairs of distinct sides that are congruent.

Triangle Congruence

The condition when two triangles are congruent based on specific criteria.

SSS Postulate

Side Side Side postulate, stating that if three sides of two triangles are congruent, the triangles are congruent.

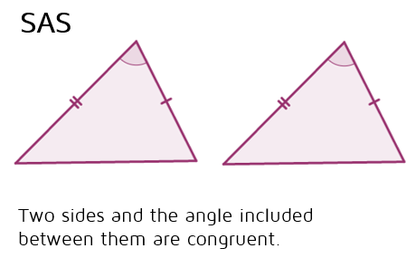
SAS Postulate

Side Angle Side postulate, stating that if two sides and the included angle of two triangles are congruent, the triangles are congruent.

AAS Postulate

Angle Angle Side postulate, stating that if two angles and a non-included side of two triangles are congruent, the triangles are congruent.

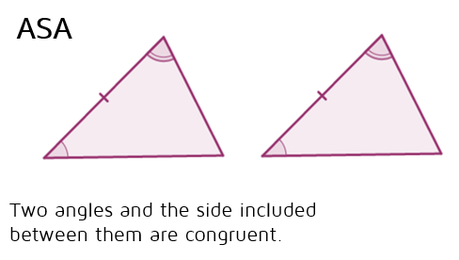
ASA Postulate

Angle Side Angle postulate, stating that if two angles and the included side of two triangles are congruent, the triangles are congruent.

CPCTC

Corresponding parts of congruent triangles are congruent.

LL Theorem

Leg Leg Theorem, stating that if the legs of two right triangles are congruent, the triangles are congruent.

LA Theorem

Leg Angle theorem, stating that if a leg and an acute angle of two right triangles are congruent, the triangles are congruent.

HL Theorem

Hypotenuse Leg theorem, stating that if the hypotenuse and a leg of two right triangles are congruent, the triangles are congruent.

HA Theorem

Hypotenuse Angle theorem, stating that if the hypotenuse and an acute angle of two right triangles are congruent, the triangles are congruent.

Similarity

A condition where corresponding sides are proportional and corresponding angles are congruent.

AA Postulate

Angle Angle postulate, stating that if two corresponding angles are congruent, the triangles are similar.

SSS Similarity

Side Side Side postulate for similarity, stating that if the lengths of all three sides of two triangles are proportional, the triangles are similar.

SAS Similarity

Side Angle Side postulate for similarity, stating that if two sides of two triangles are proportional and one angle is congruent, the triangles are similar.

To get similarity…

Get the corresponding sides and divide, they should all equal to the same fraction which is their proportion ratio.

45-45-90

1 : 1 : √2

hypotenuse = legs(√2)

legs = hypotenuse/√2

30-60-90

1 : √3 : 2

hypotenuse = shorter leg(2)

long leg = short leg(√3)

short leg = hypotenuse/2
short leg = long leg/√3

CENTER

The middle of the circle

CHORD

A line that does not pass through the radius and is contained in the circle

DIAMETER

Half of the circle, arc of a diameter is a semi circle of 180 degrees.

RADIUS

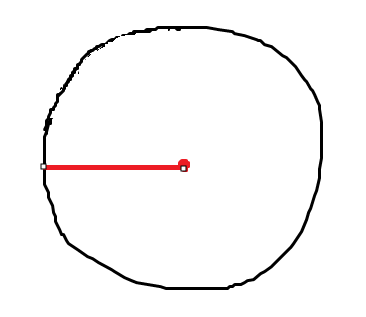
TANGENT AND TANGENT POINT

A line that touches the circle at

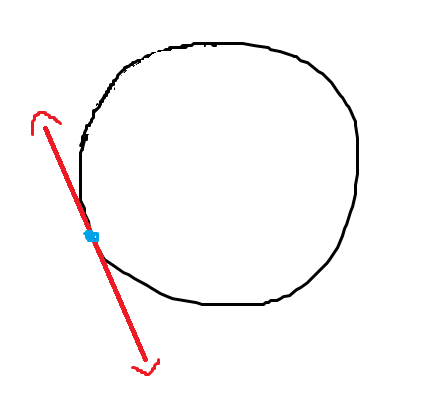
SECANT

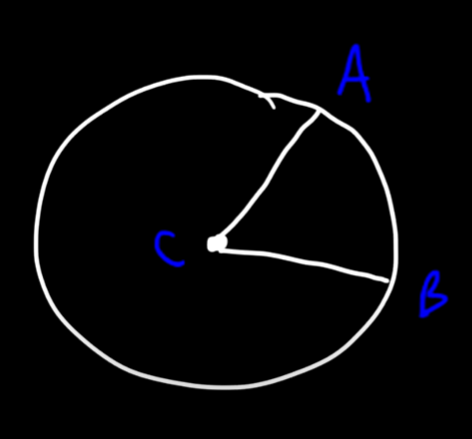
CENTRAL ANGLE

An angle that includes the center. The measure of the intercepted arc (AB) is equal to the center angle (C).

<ACB = 50 degrees
m AB = 50

INSCRIBED ANGLE

It’s an angle where the vertex is not on the center of the circle and instead is on the circle itself. So it’s made up of 2 chords, AB and BC with arc AC.

<ABC = 30 degrees
m AC = 60 degrees (ABC*2 = AC)

*The arc is twice the angle value

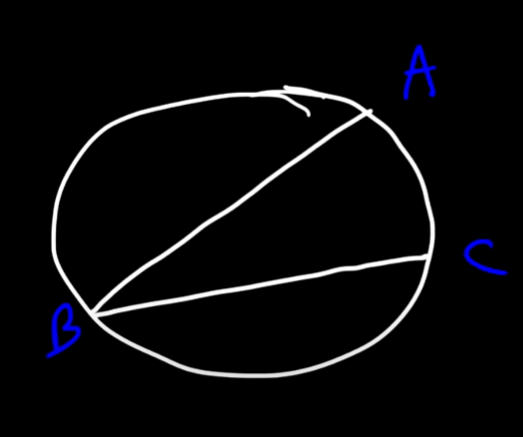
TANGENT-CHORD ANGLE

<ABC = 25 degrees
m AB = 50 degrees

*Arc is twice the value of a tangent chord angle

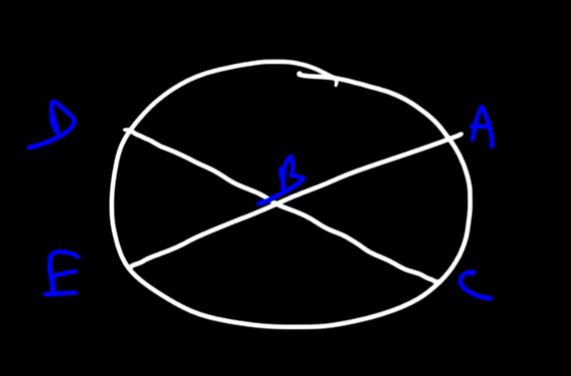
CHORD-CHORD ANGLE

<DBE = <ABC are vertical angles so they’re congruent.

m<ABC and m <DBE = (m AC + m DE)/2

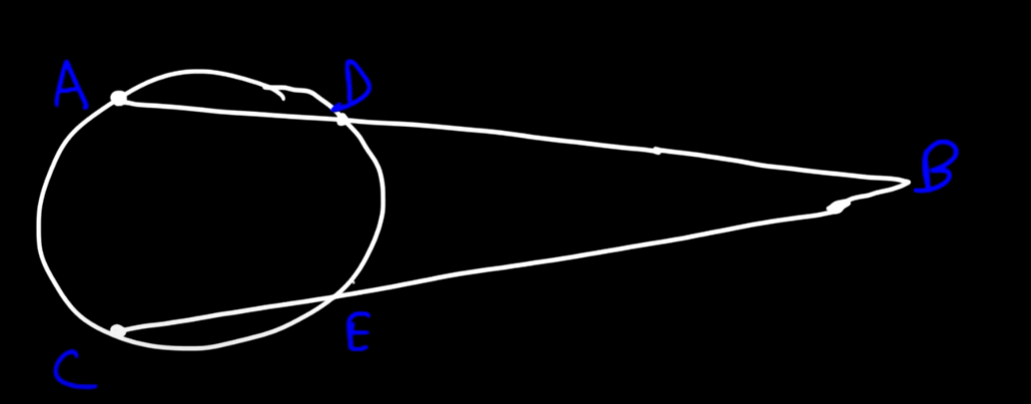
SECANT-SECANT ANGLE

Made up of 2 secant segments.

m<B = (m AC - m AD)/2

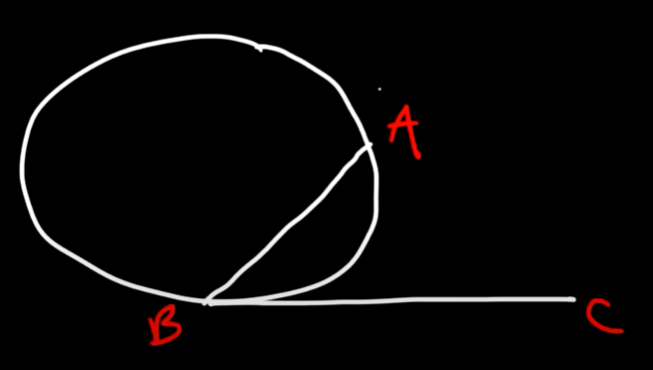
SECANT-TANGENT ANGLE

AB = Secant, CB = Tangent

Angle <B = (AC - DC)/2

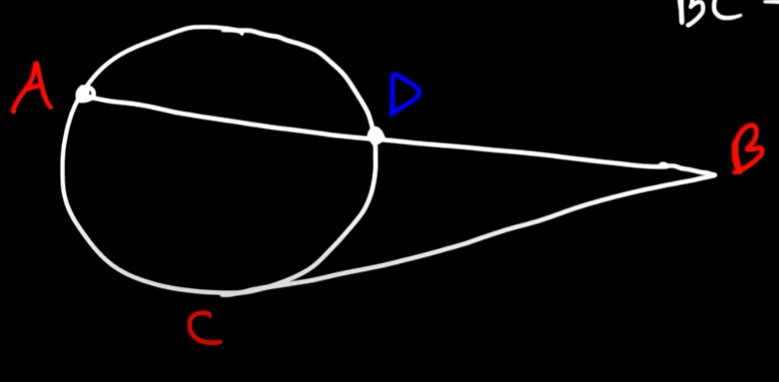
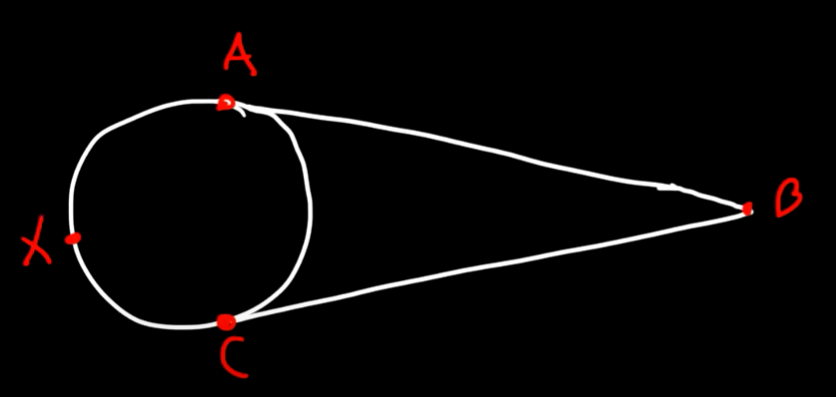
TANGENT-TANGENT ANGLE

m <B = (m AXC - m AC)/2

REMEMBER

• Arc and angle are equal (center angle)

• Angle is half of INTERCEPTED arc (inscribed angle)

• Angle is (arc + arc)/2 (Chord-chord angle)

• angle = (arc - arc)/2 (Secant-secant angle)

• angle = (S arc - T arc)/2 (Secant-tangent angle)

• angle = (arc - arc)/2 (Tangent-tangent angle)

• ALL ARCS SHOULD ADD TO 360

• SEMICIRCLES ARE ALWAYS 180

• If 2 angles share the same arc they are congruent.