Linear Algebra

What does it mean if a matrix is Singular

It does not have an inverse and it’s determinant is zero.

What is a triangular matrix

A triangular matrix is a special kind of square matrix where all the entries above or below the main diagonal are zero. There are two types: upper triangular matrices, with zeros below the diagonal, and lower triangular matrices, with zeros above the diagonal.

What do we know about the determinant of a triangular matrix?

The determinant of a triangular matrix is equal to the product of its diagonal entries.

What are the row operation rules for determinants?

1. Row swap: flips the sign of the determinant.

2. Row scaling (multiply a row by k): multiplies the determinant by k.

3. Row replacement (add a multiple of one row to another): determinant stays the same.

So:

• If you only use row replacement, the determinant is unchanged.

• If you also do row swaps or scaling, then you must adjust for those effects.

What is det(AB)?

What is det(A) det(B)?

What is det(cA)?

cⁿdet(A)

What’s det(A^-1)

1/det(A)

What does it mean to be “skew symmetric”

A matrix A is considered skew symmetric if A^T = -A, meaning its transpose is equal to the negative of the matrix itself.

What is Cramer’s Rule

It’s a special law used to help solve systems of equations in the form: x_i = det(A_i)/det(A) Where A_i is the original matrix A with column i replaced by the solution to the system.

What is a subspace?

A subspace is a subset of a vector space that is closed under vector addition and scalar multiplication, meaning it contains the zero vector and is itself a vector space.

What does it mean to span a set of vectors?

To span a set of vectors means to form a vector space by combining them through linear combinations, such that any vector in the space can be expressed as a linear combination of those vectors.

What are the vector space axioms?

The vector space axioms are a set of rules that define the structure of a vector space. They include properties such as closure under addition and scalar multiplication, the existence of an additive identity, and the existence of additive inverses.

What is a subspace?

A subspace is a non-empty subset of a vector space that is closed under addition and scalar multiplication, satisfying the vector space axioms.

How do you prove that a transformation is a linear transformation?

To prove that a transformation is linear, you need to show that it satisfies two properties: additivity, where any the transformed sum of any two vectors is equal to the sum of each vector transformed individually (T(u + v) = T(u) + T(v) for all vectors u and v), and homogeneity, where the transformation of the scalar multiple of any vector is equal to the scalar multiple of that same vector transformed (T(cu) = cT(u)) for any scalar c and vector u. The intuition to get here is that a linear transformation is one where the output is a linear combination of the inputs for all inputs.

What is the change of basis matrix?

The change of basis matrix is a matrix that represents the coordinates of vectors in one basis relative to another basis in a vector space. It allows for the transformation of vector representations when switching from one basis to another. Multiplying the change of basis matrix by any vector in the original basis will give you that vector in the new basis (in terms of the new basis coordinates)

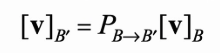
How do we find the change of basis matrix

To find the change of basis matrix, we express each vector of the new basis in terms of the old basis and form a matrix where each column corresponds to these vector representations.