Chemistry 211 - Exam 3 Prep (GMU, Dr. Fayissa)

Spring 2024 Semester

Particle

Localized energy

• Mass

• Momentum

• KE and PE

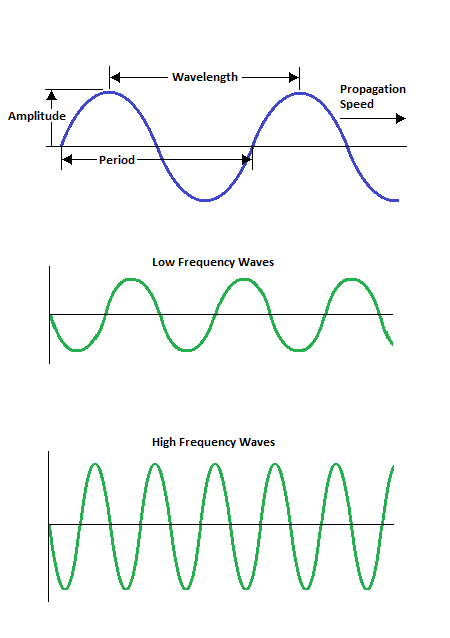
Wave

Continuous distribution of energy

• Frequency (v)

• Wavelength (λ)

• Speed (c)

• Amplitude (A)

When a wave hits a clear medium (like water)

it refracts because the speed of light changes which bends the path

When a particle hits a clear medium (like water)

the speed continues to change gradually

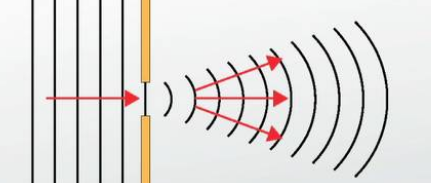
When a wave hits a small opening

it creates a semicircular wave coming out the other side (diffraction)

When a beam of particles hits a small opening

only what hit the opening go directly through to the other side, the rest is blocked

When a wave hits two small openings

it creates 2 semicircular waves thats can have both constructive and destructive interfrence with each other

Diffraction

Diffuses light/waves as it moves through a gap, leads to interference

Refraction

Bending light as it passes through something, think straw in water

Diffusion

Scattering light as it passes through something, think light through a prism = rainbow

Wavelength

Distance per cycle, λ

Frequency

Cycles per second, v

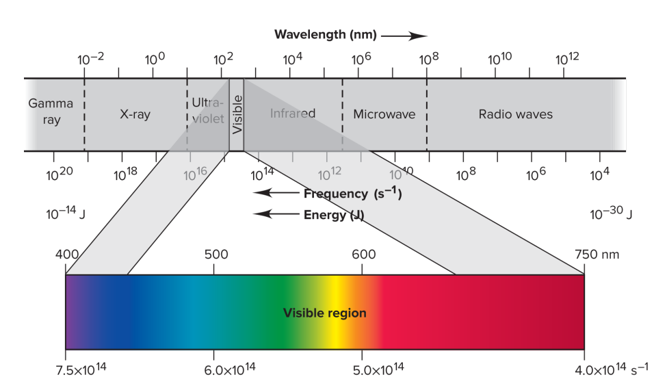
Electromagnetic Spectrum

This spectrum is the full range of electromagnetic radiation, organized by frequency or wavelength

• Raging

• Martians

• Invaded

• Venus

• Using

• X-ray

• Guns

Blackbody Radiation

Visible light when a solid is heated to 1000K, color and intensity change with temperature

Temperature

is energy

Color

is determined by wavelength and frequency

Energy of a Photon Equation

E = nhv

AND

E = hc/λ

where,

• n = postive integer

• h = Planck’s constant

• v = frequency

• c = speed of light

• λ = wavelength

Speed of Light

299,792,458 m/s

Plank’s Constant

6.626×10^-23 J/s

Quantum Theory

• LIMITs to how much energy something can emit or absorb

• Quantized = fixed quantities for energy values

• Change energy states either emit/absorb energy

Energy is directly proportional to

frequency of a wave

Energy is inversely proportional to

wavelength of a wave

Photoelectric Effect

• Threshold frequency

• Frequency determines whether electrons are released

• No time lag

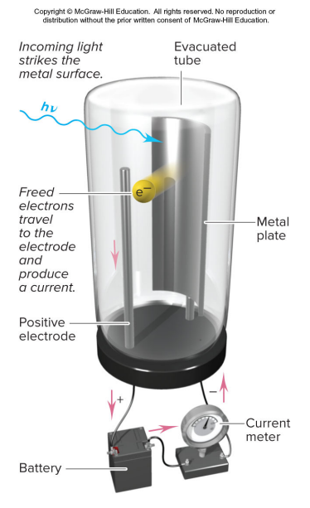
Energy of a Photon (Metal)

hv = Φ + (1/2)mv²

where:

• hv = energy of a photon

• Φ = binding energy of a electron to a metal surface, different for each metal

• m = mass

• v = velocity

Spectral Lines of Atomic Hydrogen

The line spectrum emitted by a hydrogen atom when an excited hydrogen atom returns to its ground state.

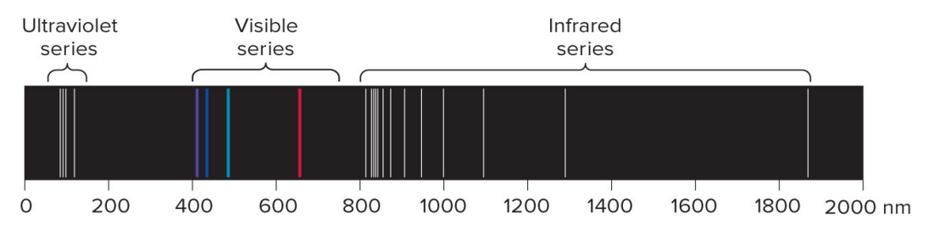
Rydberg Equation

A mathematical formula to determine the wavelength of light emitted by an electron moving between the energy levels of an atom. This equation doesn’t explain why line spectra occurs.

where:

• n₂ > n₁

• If n₁ =

  • 1: UV

  • 2: Visible

  • 3: Infrared

• R = Rydberg constant, 1.0967×10⁷ m^-1

• λ = wavelength

Issues with Rutherford

• Positive nucleus is supposed to attract negative electrons, but it doesn’t

• Contradicts classical physics

• Supposed to be a continuous specrtra, like an ombre, not like the actual hydrogen line spectra

Bohr fixes Rutherford Issues

• Planck + Einstein = quantized energy

• Stationary states

  • Hydrogen only has certian energy levels, and they have fixed orbits

  • Higher level is further from nucleus, but further is less stable

  • 1st orbit is ground state

Change of Energy of a Photon

E_Photon = E_Final - E_Initial= hv

• hv = energy of a photon

• No energy emitted in stationary states

• Jumping states emit or absorb photons

  • Higher than n=1 (ground state) is an excited state

Quantum Staircase

• Space between levels get smaller as you get farther away from the nucleus

• Highest frequency needed to go from n=1 to n=2

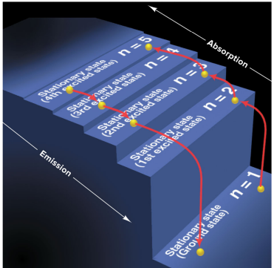
Photon Absorbtion

Lower energy level to higher energy level

EX: n=2 > n=4

Photon Emission

Higher energy level to lower energy level

EX: n=3 > n=1

Bohr Model Equation

where:

• z = charge of nucleus

• n = energy of ground state

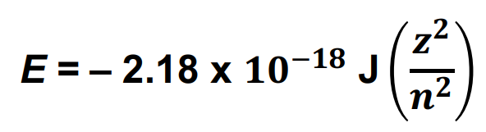
Matter/Energy Equation

e = mc²

where:

e = energy

m = mass

c = speed of light

De Broglie Wavelength

h = Plank’s Constant, 6.626×10^-34 J*s

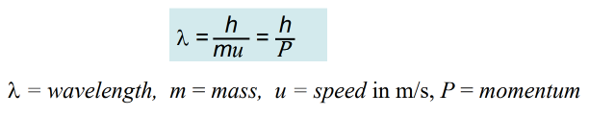
Heisenburg’s Uncertainty Principle

Can’t know both position and speed at the same time

If we know one, the other becomes less certain and vice versa

Quantum Mechanics

Wave nature of objects on the atomic scale

Schrodinger’s Wave Equation (Quantum Mechanics)

HΨ = EΨ

where:

• H = Hamiltonian Operator (Total Energy of a System, KE + PE)

• Ψ = Wave function is atomic orbital

• E = Energy

• Ψ² = Probabilty density, the measure of the probability of finding an electron in some tiny volume of the atom

• Solveable for hydrogen, not for many-electron atoms

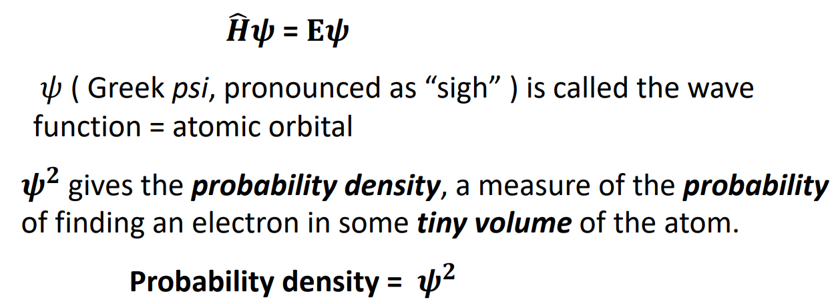
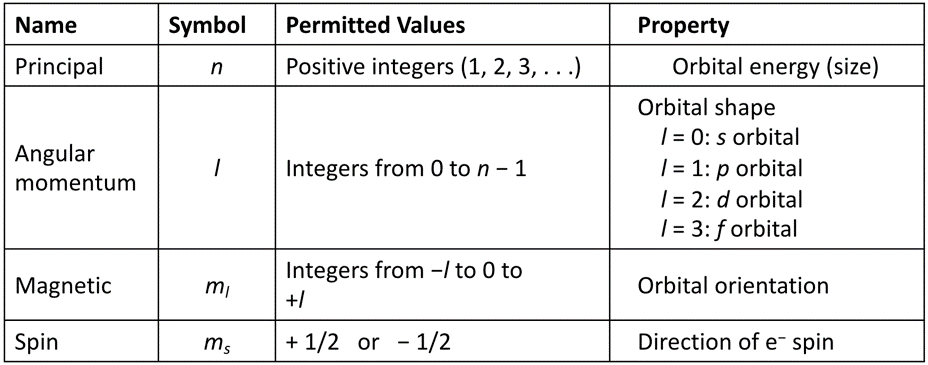
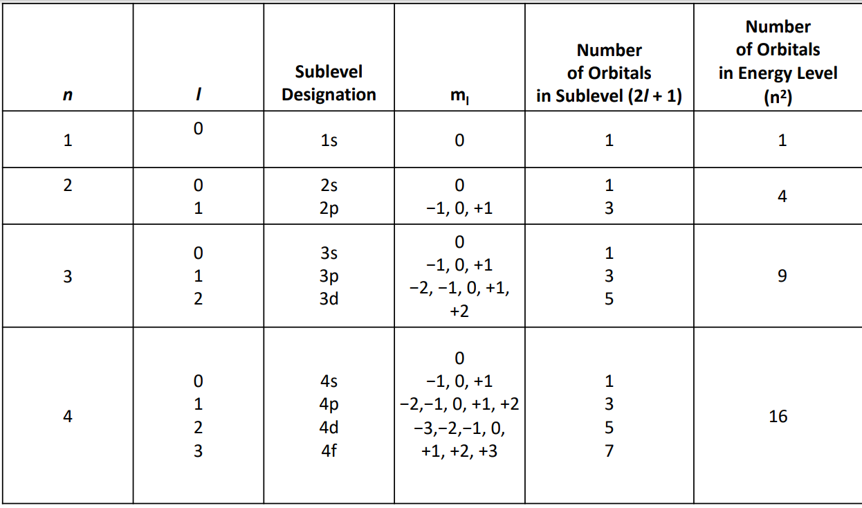
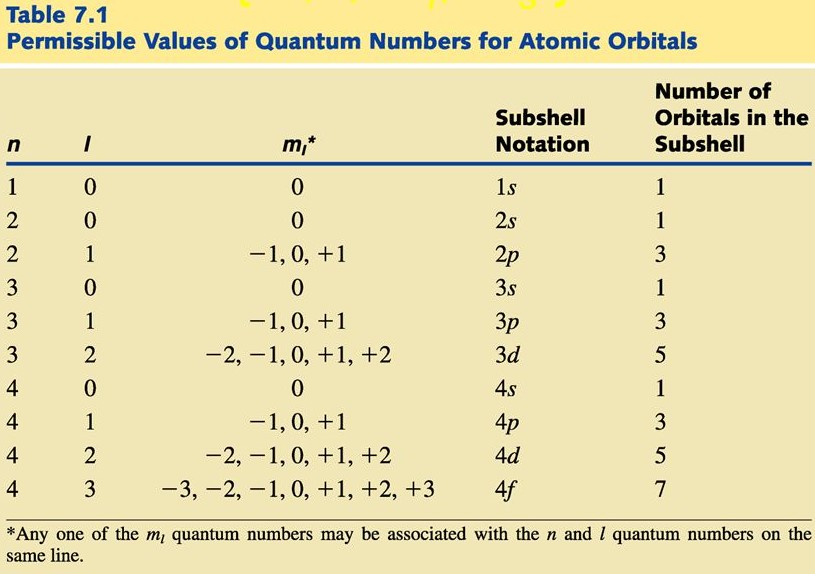
4 Quantum Numbers

• Principle (n)

  • Always postive

  • Relative size and distance from nucleus

  • Energy

• Angular Momentum (l)

  • Any number from 0 to (n-1)

  • Shape

• Magnetic (m_l)

  • -l

  • -l+1

  • 0

  • l+1

  • l

  • Orientation

• Spin (m₂)

  • +1/2

  • -1/2

  • Direction of electron spin

n, l, m Chart

Pauli Exclusion Principle

1. Each atom is described completely by the four quantum numbers

2. No atom in an element will have the exact same 4 numbers

3. An atomic orbital can hold a maximum of two electrons and they have opposite spins.

Factors Affecting Atomic Orbital Energies

1. Nuclear charge

2. Shielding Effect

3. Orbital shape

As a element gets bigger the closer electrons get pulled more closely, while the farther away electrons are not pulled as tightly due to shielding and being farther away from the nucleus.

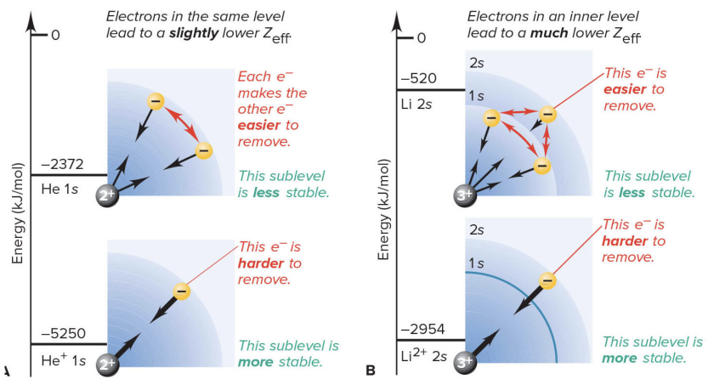
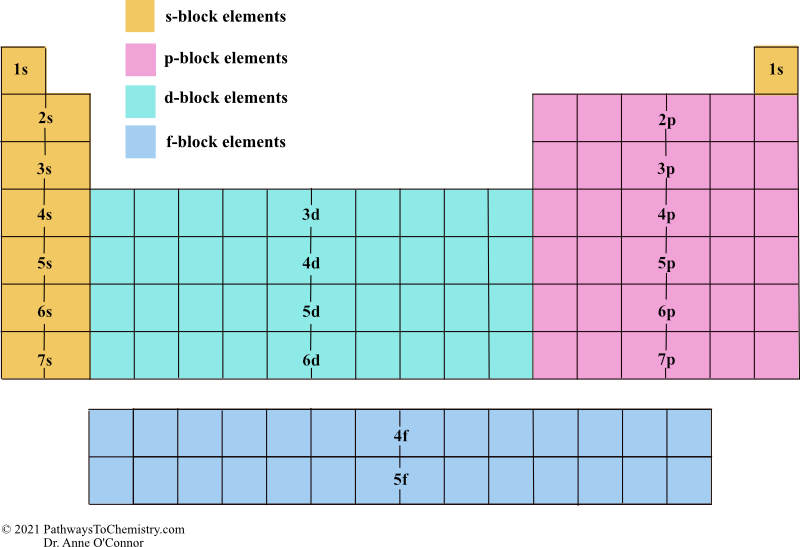
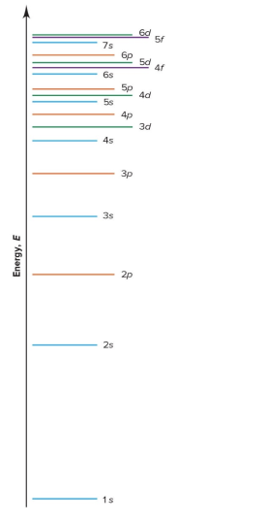
Sublevel Energy Levels

s < p < d < f  in energy

Ground State Electron Configuration Example

Electron Configuration Chart

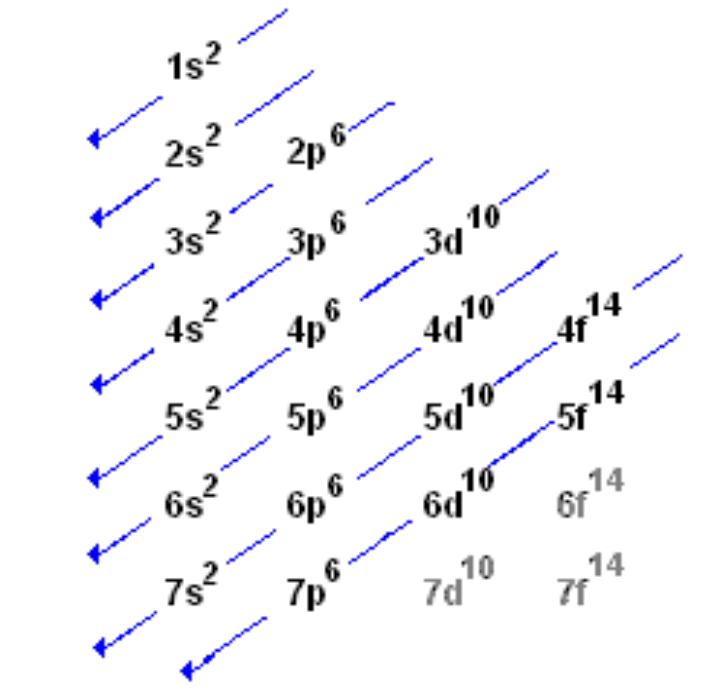
Ground State for Elements and Their Electrons

The most stable state for an element, which can be found from the periodic table (all elements are in these states on the periodic table)

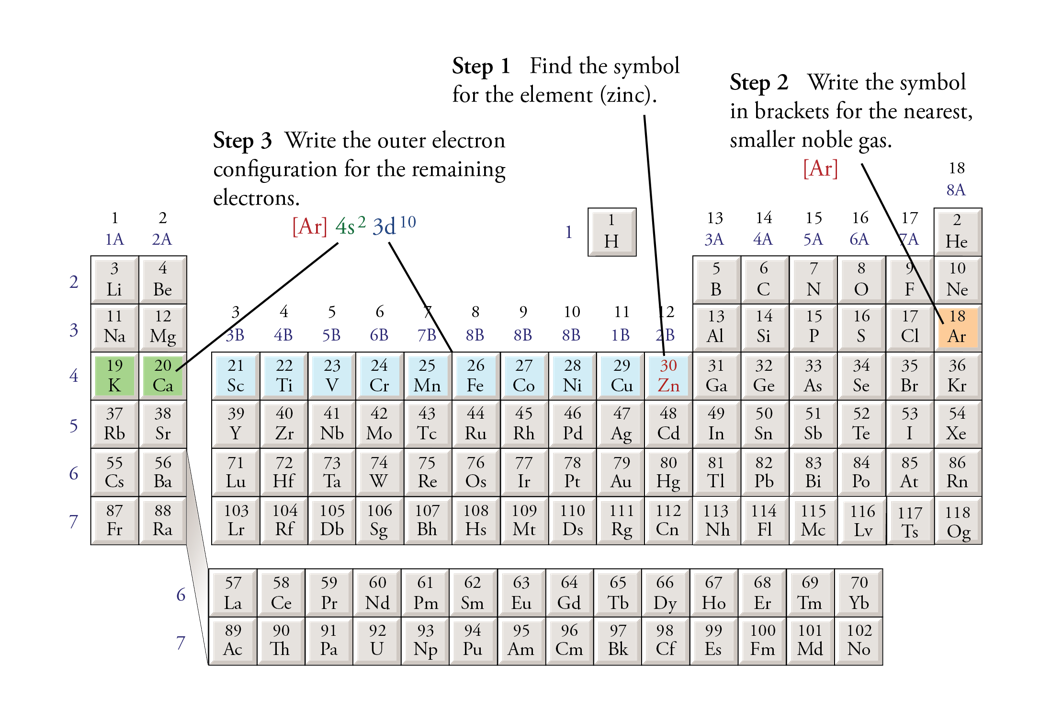
Condensed Electron Configuration

1. Find the element on the table

2. Write the symbol in brackets for the nearest, smaller noble gas

3. Subtract the amount of electrons for the noble gas from the element you are writing for

4. Write the electron config for those remaining atoms

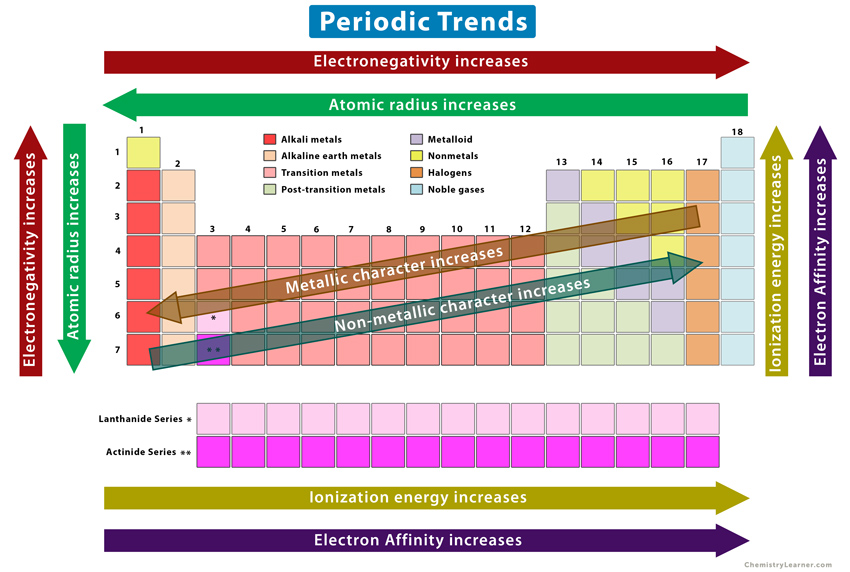
Atomic Radius Trend

Increases DOWN a column

Increases to the LEFT of a period

Ionization Energy Trend

Increases UP a column

Increases to the RIGHT of a period

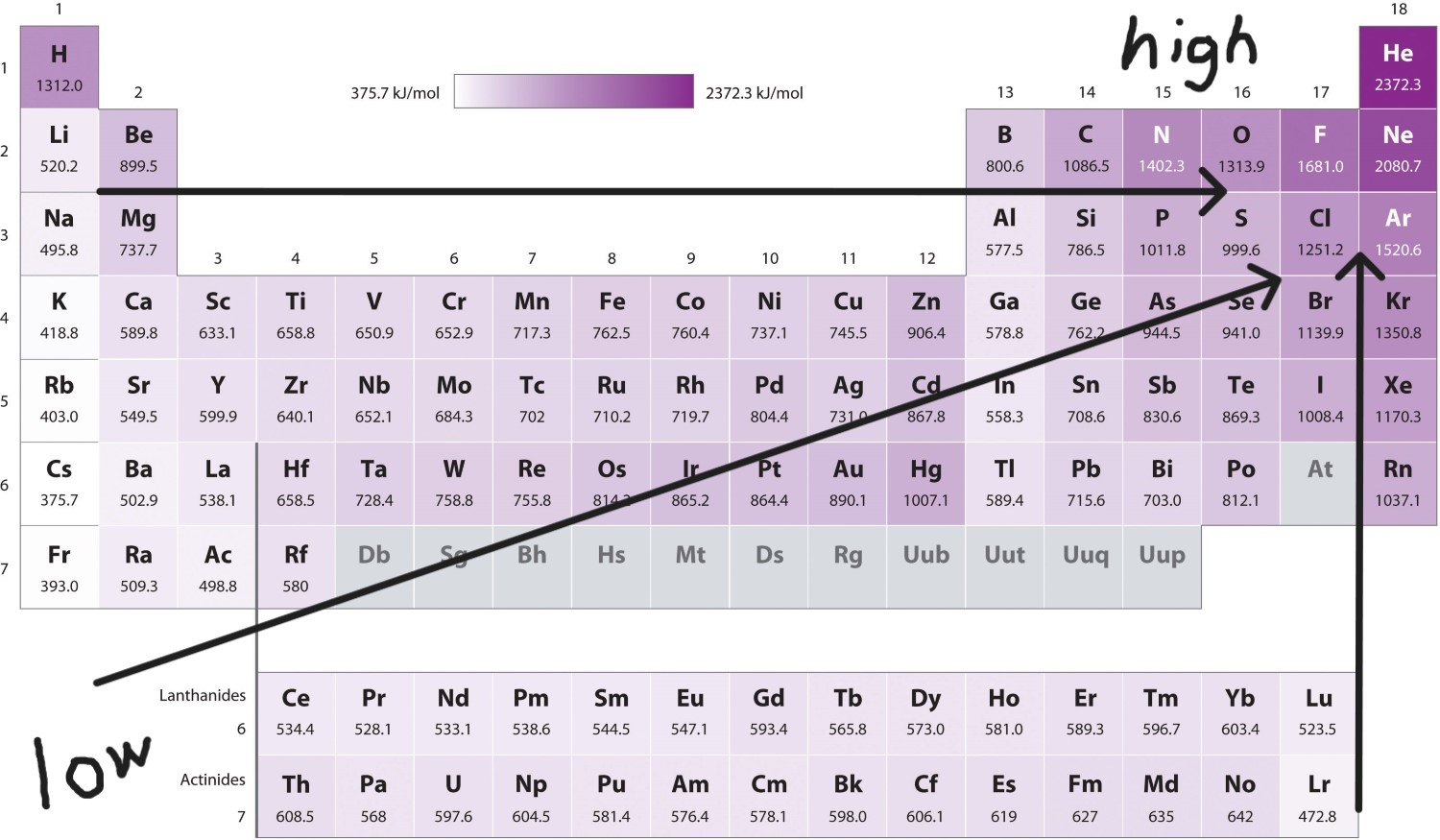
Electron Affinity Trend

Increases UP a column

Increases to the RIGHT of a period

(with many exceptions for both)

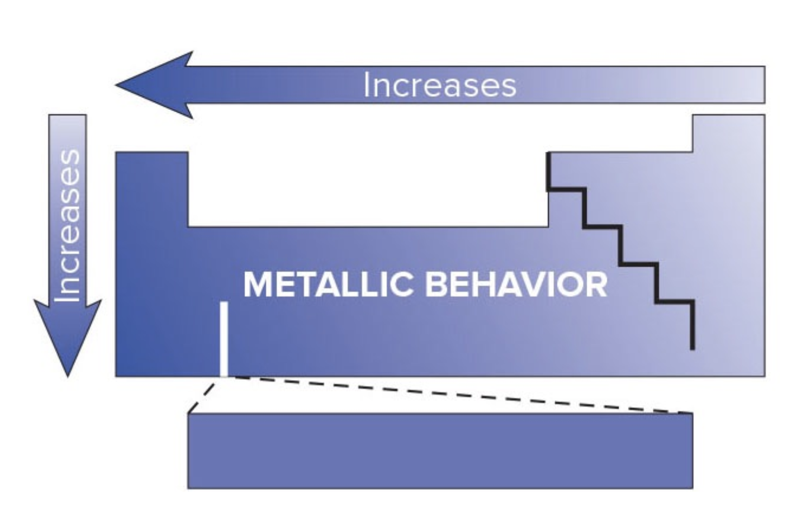
Metalic Behavior Trend

Increases DOWN a column

Increases to the LEFT of a period

Ionic Bonding

Bond between metal and nonmetal, the metal transfers an electron to the nonmetal, a strong bond

Covalent Bonding

Sharing of electrons between two nonmetals, a weak bond

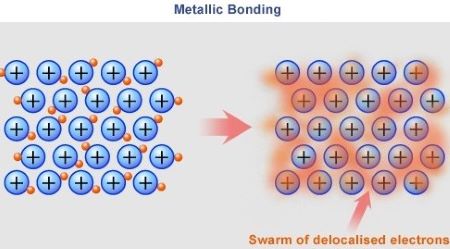
Metallic Bonding

A type of chemical bond similar to a covalent bond. Atoms in metals are held together by forces caused by the valence electrons. Electrons float freely around metalic ion cores.

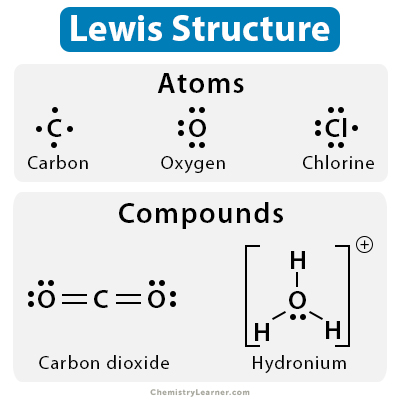
Lewis Dot Diagram

Representation of valence electrons.

• - is a pair electron bond between two elements

• = is a double pair electron bond between two elements

• Each dot represents an electron

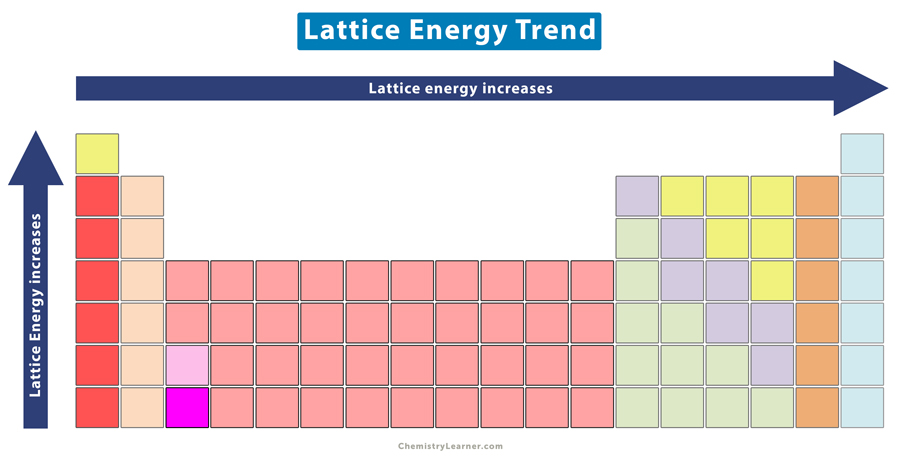
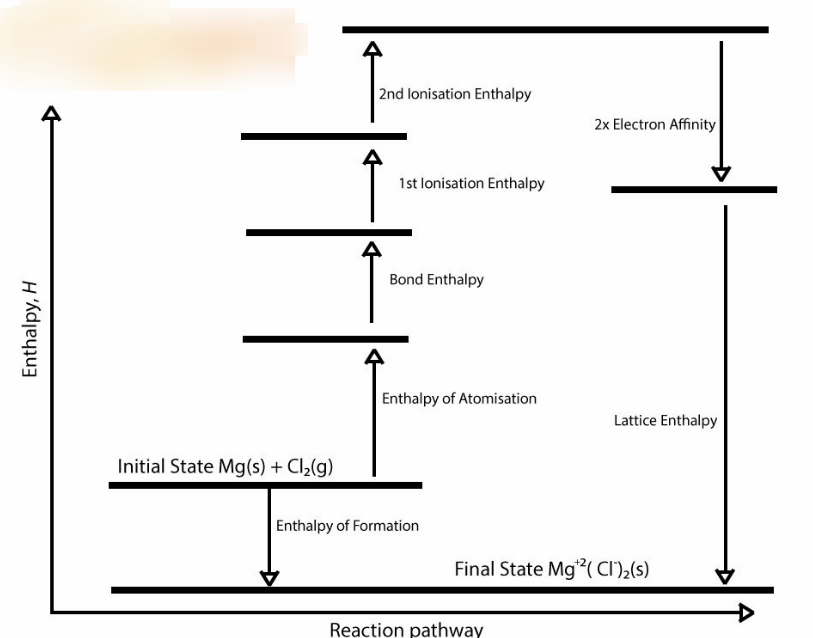
Lattice Energy Trend

Lattice energy: the energy required to separate 1 mol of an ionic solid into gaseous ions.

• As ionic size increases, lattice energy decreases.

• As  ionic charge increases, lattice energy increases.

Coulomb’s Law

k(Q1*Q2 / r1 + r2)

where:

• k = Coulomb’s constant

• Q1 = Charge of particle 1

• Q2 = Charge of particle 2

• r1 = Particle 1 radius

• r2 = Particle 2 radius

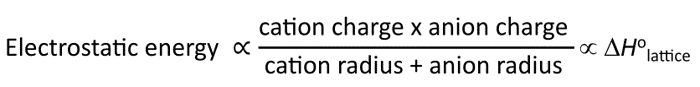
Covalent Bond Properties

• Bond Order

  • The number of electrons being bonded.

  • EX:

    • Bond Order 1 = Single Bond

    • Bond Order 2 = Double Bond

    • Bond Order 3 = Triple Bond

• Bond Energy

  • Energy needed to overcome the attraction between the nuclei and shared electrons. The stronger the bond, the higher the bond energy.

    • Higher bond order = more bond energy

    • Lower bond order = less bond energy

• Bond Length

  • The distance between the nuclei of bonded atom

    • Higher bond order = shorter length (3)

    • Lower bond order = longer length (1)

Enthalpy of a Reaction

Change in H of Reaction = Change in H of Reactant Bonds - Change in H of Product Bonds

You basically subtract the H of products from the H of Reactants to find your H of the whole reaction

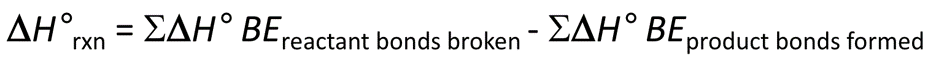
Electronegativity Trends

Increases UP a column

Increases to the RIGHT of a period

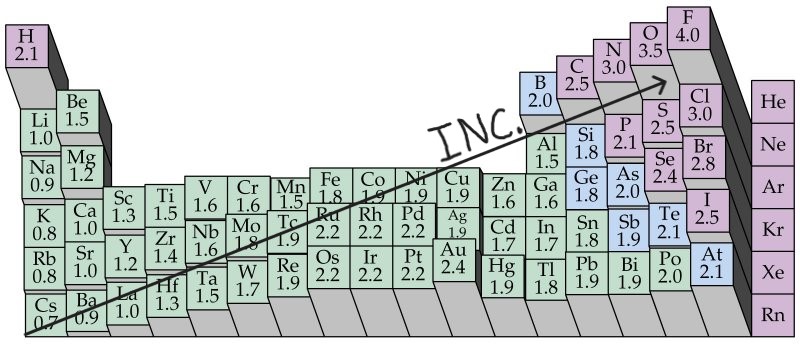
Bond Polarity / Ionic Character

The greater the difference in electronegativities between two bonded atoms, the greater the polarity / Ionic Character of the bond

Metallic and Non-Metallic Character

Diamagnetic Elements

Elements that have all of their electrons paired up in their electron configuration.

Paramagnetic (Non-Diamagnetic)

Elements that have one or more unpaired electrons in their electron configuration.

Quantum Numbers for Oribitals

• S: l = 0, m1 = 0

• P: l = 1, m1 = -1, 0, +1

• D: l = 2, m1 = -2, -1, 0, +1, +2

• F: l = 3, m1 = -3, -2, -1, 0, +1, +2, +3

Lattice Enthalpy Energy Diagram

All Periodic Table Trends

SPDF Blocks Periodic Table