Geometry H - Postulates, Theorems, Laws, Formulas

ruler postulate

Every point on a line can be paired with a real number. This

makes a one‐to‐one correspondence between the points on

the line and the real numbers.

segment addition postulate

If three points A, B and C are collinear and B is between A and

C, then AB + BC = AC.

protractor postulate

The measure of an angle is the absolute value of the difference of its ray.

angle addition postulate

two adjacent angles can be added together to form a larger angle.

What info can you assume from a diagram?

1. adjacent angles

2. vertical angles

3. supplementary

What info can’t you assume from a diagram?

1. congruent angles or segments

2. right angles

3. complementary angles

linear pair postulate

If two angles form a linear pair, then they are supplementary.

midpoint formula

a+b/2

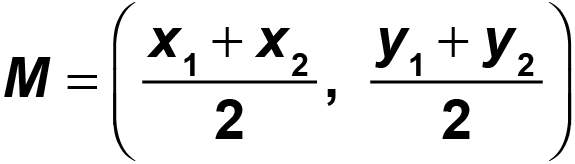
distance formula

perimeter

• square = 4s

• triangle = a+b+c

• rectangle = 2L+2W

The sum of the sides.

area

• square = s²

• triangle = ½ bh

• circle = πr²

• rectangle = LW

negation

opposes the truth value. (~)

conjunction

• “and” statement (∧)

• both have to be true to be true

• p∧q

disjunction

• “or” statement (∨)

• one has to be true to be true

• p∨q

conditional

• “if, then…” statement

• always true except when p is true and q is false.

• logically equivalent to contrapositive

• p→q

inverse

negate p and q

• ~p→~q

converse

switch p and q

• q→p

contraposititve

• switch AND negate p and q.

• logically equivalent to conditional

• ~q→~p.

biconditional

• “if and only if” statement

• both p and sue have to be both false or both true to be true.

• p↔q

addition property of equality

If a=b, then a+c = b+c.
Adding the same number to both sides of an equation keeps the equation balanced.

subtraction property of equality

If a = b, then a - c = b - c.
Subtracting the same number from both sides of an equation keeps the equation balanced.

multiplication property of equality

If a = b, then a · c = b · c (for any c ≠ 0).
Multiplying both sides of an equation by the same nonzero number keeps the equation balanced.

division property of equality

• If a = b, then a / c = b / c (for any c ≠ 0).
  Dividing both sides of an equation by the same nonzero number keeps the equation balanced.

reflexive property of equality

a = a.
Any number or expression is always equal to itself.

transitive property of equality

If a = b and b = c, then a = c.
If two things are equal to the same thing, they are equal to each other.

substitution property of equality

If a = b, then a can be substituted for b in any expression.
If two quantities are equal, one can replace the other in any equation or expression.

symmetric property of equality

If a = b, then a can be substituted for b in any expression.
If two quantities are equal, one can replace the other in any equation or expression.

distributive property of equality

a(b + c) = ab + ac.
Multiplying a number by a sum is the same as multiplying the number by each term in the sum and adding the products.

reflexive property of congruence

AB ≅ AB or ∠A ≅ ∠A
Any geometric figure is congruent to itself.

symmetric property of congruence

If AB ≅ CD, then CD ≅ AB.
If one figure is congruent to another, the second figure is congruent to the first.

transitive property of congruence

If AB ≅ CD and CD ≅ EF, then AB ≅ EF.
If two figures are each congruent to a third figure, they are congruent to each other.

vertical angles theorem

Vertical Angles are congruent.

congruent supplements theorem

If two angles are supplements of the same angle (or congruent

angles), then the two angles are congruent.

right angle theorem

All right angles are congruent.

congruent complements theorem

If two angles are complements of the same angle (or congruent

angles), then the two angles are congruent.

same side interior angles postulate

If a transversal intersects two parallel lines, then the same‐side

interior angles are supplementary.

corresponding angles theorem

If a transversal intersects two parallel lines, the corresponding

angles are congruent.

alternate interior angles theorem

If a transversal intersects two parallel lines, then alternate

interior angles are congruent.

alternate exterior angles theorem

If a transversal intersects two parallel lines, then alternate

exterior angles are congruent.

converse of corresponding angles theorem

If two lines and a transversal form corresponding angles that

are congruent, then the lines are parallel.

converse of same side interior angles postulate

If two lines and a transversal form same‐side interior angles

that are supplementary, then the two lines are parallel.

converse of alternate interior angles theorem

If two lines and a transversal form alternate interior angles that

are congruent, then the two lines are parallel.

converse of alternate exterior angles theorem

If two lines and a transversal form alternate exterior angles

that are congruent, then the two lines are parallel.

triangle angle-sum theorem

The sum of the measures of the angles of a triangle is 180.

triangle exterior angle theorem

The measure of each exterior angle of a triangle equals the sum

of the measures of its two remote interior angles.

third angles theorem

If the two angles of one triangle are congruent to two angles of

another triangle, then the third angles are congruent.

sss postulate

If three sides of one triangle are congruent to three sides of

another triangle, then the two triangles are congruent.

sas postulate

If two sides and the included angle of one triangle are

congruent to two sides and the included angle of another

triangle, then the two triangles are congruent.

asa postulate

If two angles and the included side of one triangle are

congruent to two angles and the included side of another

triangle, then the two triangles are congruent.

isosceles triangle theorem

If 2 sides of a triangle are congruent, then the angles opposite those sides are congruent.

converse of isosceles triangle theorem

if two angles of a triangle are congruent, then the sides opposite those angles are congruent

perpendicular bisector of base theorem

if the line bisects the vertex angle of an isosceles triangle, then the line is a perpendicular bisector of the bases.