psych 218 midterm 2 - correlation

correlation coefficient exceptions ®

• If you have a curvilinear relationship, the correlation coefficient will be zero. 

  • This is bc r can only handle linear relationships 

    • This does not mean there is no relationships between the variables. 

      • There may be a non-linear relationships between the variables

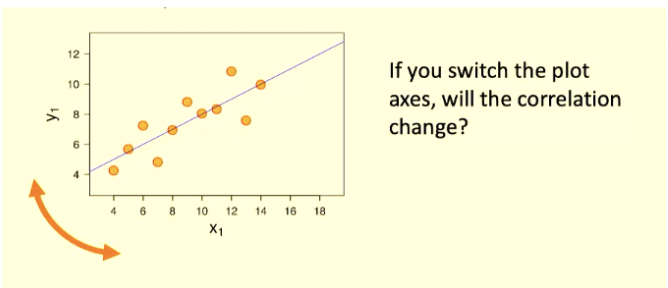
• Direction will not change. If it was positive b4 it will stay positive and vise versa 

• Magnitude will not change

• Form will not change 

• Changing the visualization will not change the relationship between the variables 

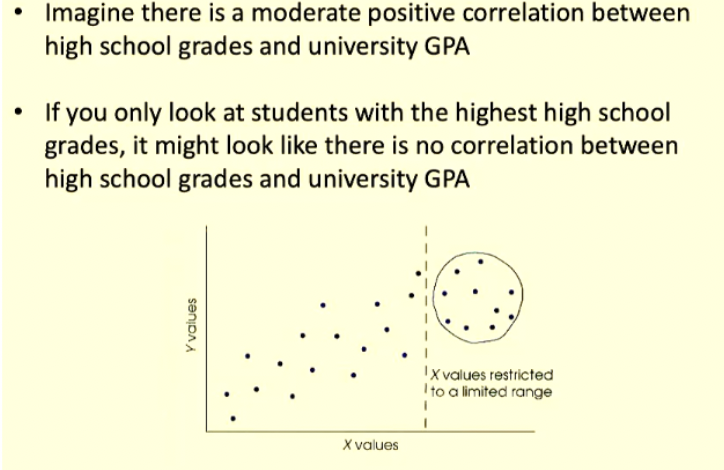
•  Range restriction 

• When you have access to only a small slice of the total data 

• can impact your interpretation of correlations as there could be a correlation when looking at the overall data but when you are range restricted you may be told there is a different correlation/interpretation

• 3 ways to calculate the pearson correlation coefficient ®

• Z score method (dont care about this one)

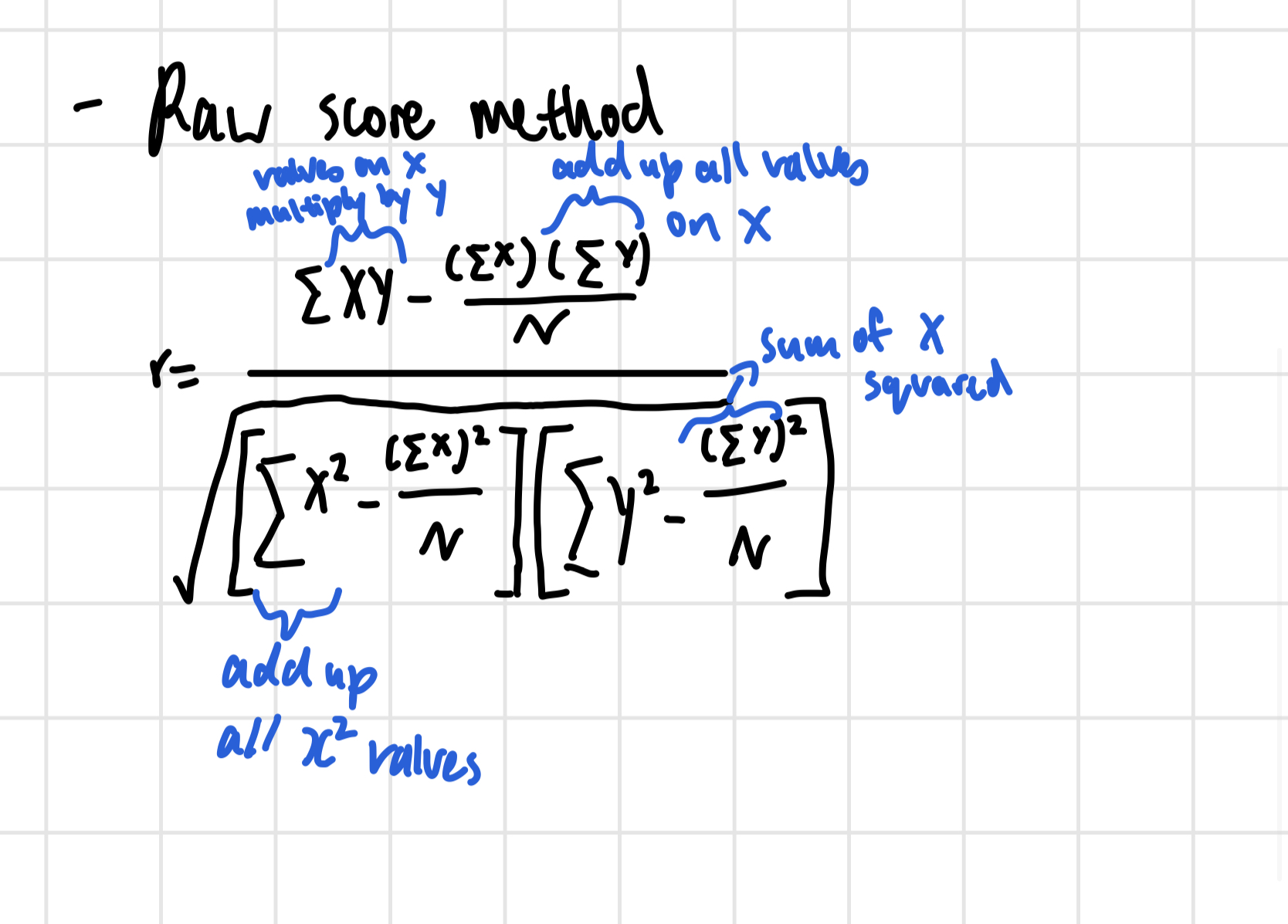
• Raw score method

• Cross product method

how to do cross product method way of calculation

how to do raw score method way of calculation

• How big is the correlation 

• • If r is 0 → no relationship 

  • If r is between 0 and 0.10 → trivial relationship 

  • If r is between 0.10 and 0.30 → small to medium relationship 

  • If r is between 0.30 and 0.50 → medium to large relationship 

  • If r is greater than 0.50 → there is a large to very large relationship 

If relationship is curvilinear, the correlation coefficient ———-, can be used to describe the strength of the relationship

(eta → ‘ey-tah’)

What can you conclude from correlations?

• A correlation can tell you about the relationship between 2 variables but it cannot tell you about causality 

• It can be exploratory → be a starting point for more research 

• Correlations can help when there are ethical constraints. → there are certain variables that are unethical to manipulate so its better to use correlational designs

regression

• using correlations to predict and account for differences in scores

• How much can we explain (in terms of accounting for variability)

• If a correlation is perfect, all of the points line up perfectly —> We can say ‘all of the variability in Y can be accounted for by variability in X’ 

• If the correlation is less than perfect, some variability in Y cannot be accounted for by variability in X 

• r² expresses the proportion of variability that CAN be explained

r²

• To compute r^2, square the correlation (r x r) 

• Ranges from 0 to 1 (can multiply this number by 100 to get a percentage)

• Also called the ‘coefficient of determination’

• Measure of effect size 

explain the concept behind this visual

Blue square is the variability we can explain, and the remaining area is the area we cannot; we can explain 42% of the variability

Partial correlation

• The numbers 123 are all different variables when you are given variables 

• The correlation between 2 variables when the effect of a third (or fourth, etc) variable has been eliminated (or held constant) 

how to calculate partial correlation

• First calculate correlation for education and life expectancy

• then control partial correlation between education and life expectancy, controlling for IQ

• then compare the regular correlation to the partial correlation and note any differences between the two values

• If there is a difference when the 3rd variable is accounted for, thats telling you that the 3rd variable accounts for at least some of the relationship between the original pair of variables 

• 

what are correlations with binary variables

• Variables that have 2 cateogies/values 

  • Can be qualitative or quantitative variables 

  • yes/no, self/other, pass/fail, Mac/PC

• You need to apply numbers to each category (0/1, ½, etc) 

• 

• How to interpret correlation when there are binary variables 

• Line of best fit would slope upwards, suggesting a positive correlation 

• High on X is associated with high on Y (and low X with low Y) 

  • Mac = high, PC = low 

• Thus, having a mac (compared to having a PC) is associated with higher grades  

Linear transforms in terms of r²

• Linear transforms only ‘shift’ or ‘stretch’ the data but does not affect the correlation coefficient 

• Exception: multiplying one (but not both) variables by a negative number (you change it to be either positive or negative) 

• Disparate subgroups 

• Presence of distinct subgroups (age, gender, class, etc) 

• Can artificially increase or decrease correlation coefficient 

• e.g.

  

  • When you look at 1 subgroup, theres no correlation. But when you look at the entire picture, there is a positive correlation