2.18. - Proton-spin mágneses momentumok viselkedése mágneses térben. Az eredő momentum iránya és nagysága.

A protonok mágneses momentuma mágneses térben milyen kvantáltságot mutat?

A protonok mágneses momentuma mágneses térben iránykvantálást mutat. Energetikailag különböző állapotok lépnek fel. A klasszikus viselkedésű mágneses momentum energiája mágneses térben lecsökken mint azon kívül. A mágneses tér orientálja ezt a momentumot parallel irányba (mágneses tér irányítottságával párhuzamosan).

Ha E értéke csökken milyen irányba orientálja a momentumot a mágneses tér?

Ha 𝐸 értéke csökken, vagy ha a cos𝜙 nő akkor a mágneses tér orientálja a momentumot parallel és antiparallel irányba. Ezek két energiaszinttel jellemezhetőek. A parallel orientációnak mindig kisebb az energiának.

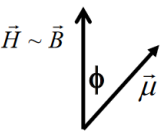
Kvantumos viselkedésű mágneses momentum milyen orientációt tud felvenni?

Kvantumos viselkedésű mágneses momentum kétféle orientációt tud felvenni, parallel és antiparallel orientációkat. Energia különbségek lesznek.

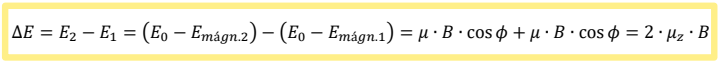
Mágneses térrel parallel és antiparallel orientált momentum vektorok eredője:

▪ Az ellentétes irányú vektorok eredője = 0!

▪ Melyikből van több? 𝑁₁ és 𝑁₂

Boltzmann eloszlás:

az alacsonyabb energiájúnívó populációja nagyobb, azaz 𝑁₁ > 𝑁₂

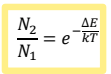
A mágneses momentumok csak nem teljesen közömbösítik egymást. ez mit eredméynez?

Az antiparallel orientációk száma alig kisebb, mint a parallelorientációké. A mágneses momentumok csak nem teljesen közömbösítik egymást. Ebből adódik, hogy az eredő vektor parallel a mágneses térrel és igen kicsi.

Mivel növelhető a ∆E?

Mag-mágneses momentumokra alapozott mérésekben igen kis effektus várható. De a gazdag információtartalom miatt mégis érdemes mérést tervezni.

Nagyobb populáció-különbség kell ami ∆𝐸-től függ, amelyet ha növelünk nő az eredő vektor is. ∆𝐸 a mágneses tér nagyságával növelhető.

Összefoglalva:

▪ 𝐵⃗ -vel (mágneses térerősség) parallel és antiparallel állásúak lehetnek

▪ a parallel orientációnak kisebb az energiája és nagyobb a populációja

▪ mindkét orientációban precesszálnak 𝒇 = 𝟏/𝒉 ∙ 𝟐 ∙ 𝝁 ∙ 𝑩 frekvenciával

▪ a parallel orientációjú energiaállapot 𝒉 ∙ 𝒇 = ∆𝑬 = 𝟐 ∙ 𝝁 ∙ 𝑩 fotonenergiával gerjeszthető (átvihető) antiparallel állapotba

▪ a két orientáció energiakülönbsége lineárisan nő B-vel

▪ az eredő mágneses momentum vektor parallel a mágneses tér irányával és nagysága |𝐵⃗ |-vel növelhető ▪ protonok eredő momentuma: ∑ 𝜇 = M