C1 - Linear Equations

Row operations

Alterations to a matrix that maintains the linear equation equivalency

• Replace, interchange, scaling

• Two row-equivalent matrices have the same solution set

Row echelon form

• Each leading entry below the last is to the right of the former’s column

• All entries below leading entry are zero

• Nonzero rows above zero rows

Reduced row echelon form

• All requirements of row echelon form

• Each leading entry must be 1

• The leading 1 is the only nonzero entry in the column

Uniqueness of echelon forms

Each matrix is row equivalent to only one RREF

Pivot position

Leading 1 in the RREF

• Pivot column contains pivot position

• Rows w/ no pivot correspond to free variables

Existence and Uniqueness Theorem

Linear system is consistent if and only if row

• [0 0 … b]

  • b = nonzero

does not appear.

Span

All possible combinations of a set of vectors

Matrix equation

Ax = b

• Linear combination of columns

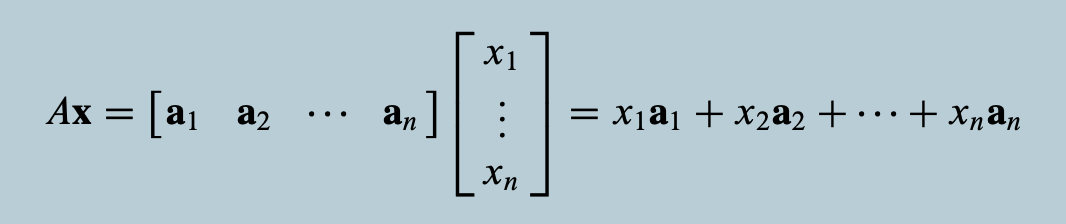
Equivalent statements for matrix equations

*For coefficient matrices

Homogeneous system

Ax = 0

Nontrivial solutions of homogeneous systems

Nontrivial solutions exist if at least one free variable exists

Parametric vector form

x = su + tv

• Parameter t

Theorem

Scalar additions of a homogeneous solution correspond to non-homogeneous solutions

Linear independence

• When a set of rows in a matrix does not have a free variable

• If and only if the only solution to a₁x₁ + a₂x₂ + … = 0 is trivial

  • Each vector adds a unique dimension

Linear dependence of zero vectors

Vector set is linearly dependent if it contains the zero vector

Transformation

Changing of any vector’s position based on how the unit vectors change

• Matrix columns can indicate this change

• Multiplying by a “transformation matrix” transforms a vector

• Change in dimensions is arbitrary

Linear transformation

T(u + v) = T(u) + T(v)

T(cu) = cT(u)

• c = scalar

Domain, range, codomain

Domain: input values

Range: output values

Codomain: dimension in which the output values exist