Specialist

Distance from point to a plane

Distance from origin to the plane

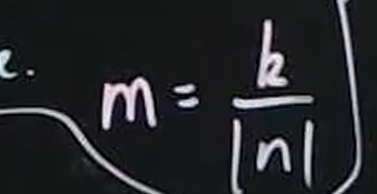
Arc Length Formula of a parametric curve

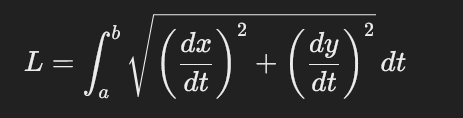
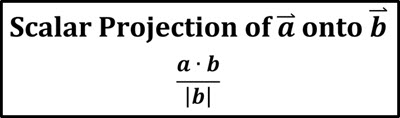
Scalar projection of a onto b

and used to find distance between two points/lines/ maybe planes

find a vector between the two points on a line
then find the normal then do the projection of that vector onto the normal as seen in the image

Maximum height of a projectile formula

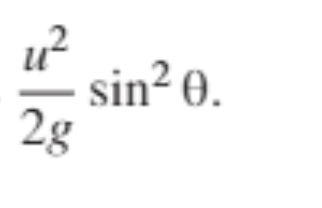
Range of a projectile formula

direction of projection

refers to the initial velocity vector of the objec

Can find angle of projection if velocity vector in i and j components is known

draw the diagram out, take tan theta of j/i

Finding time of maximum height

Set Y COMPONENT of velocity vector equals to 0

then substitute the time into the POSITION VECTOR y-component

If need to prove for odd integers use

2k+1

Inductive Hypothesis: Assume P(2k+1)P(2k+1) is true for some odd integer 2k+12k+1.

Inductive Step: Prove P(2k+3)P(2k+3) is true using the assumption for P(2k+1)P(2k+1).

Possible Induction statement

Given 𝑃(𝑘) is true, therefore 𝑃(𝑘 + 1) is true ∀𝑘 ∈ ℤ), therefore by mathematical

induction, 𝑃(𝑛) is true ∀𝑛 ∈ ℤ)

When finding coefficents or third solution to complex polynomials, you can do

(z-c), and then expand with solutions already known

then combine or GROUP like terms if there are mulitple variables, using e.g. z³ or z², z

then compare coefficents to original polynomial and solve for variables

Particle heads to y-direction/x-direction means

means either i or j component will be set to equal 0

what does initial direction mean

it means intial velocity v(o)

u is what?

u is the magnittude of the intial velocity vector

When wanting to factorise complex quadratics

complete the square then but into a²-b² form

Complex polynomial finding solutions and variables working out

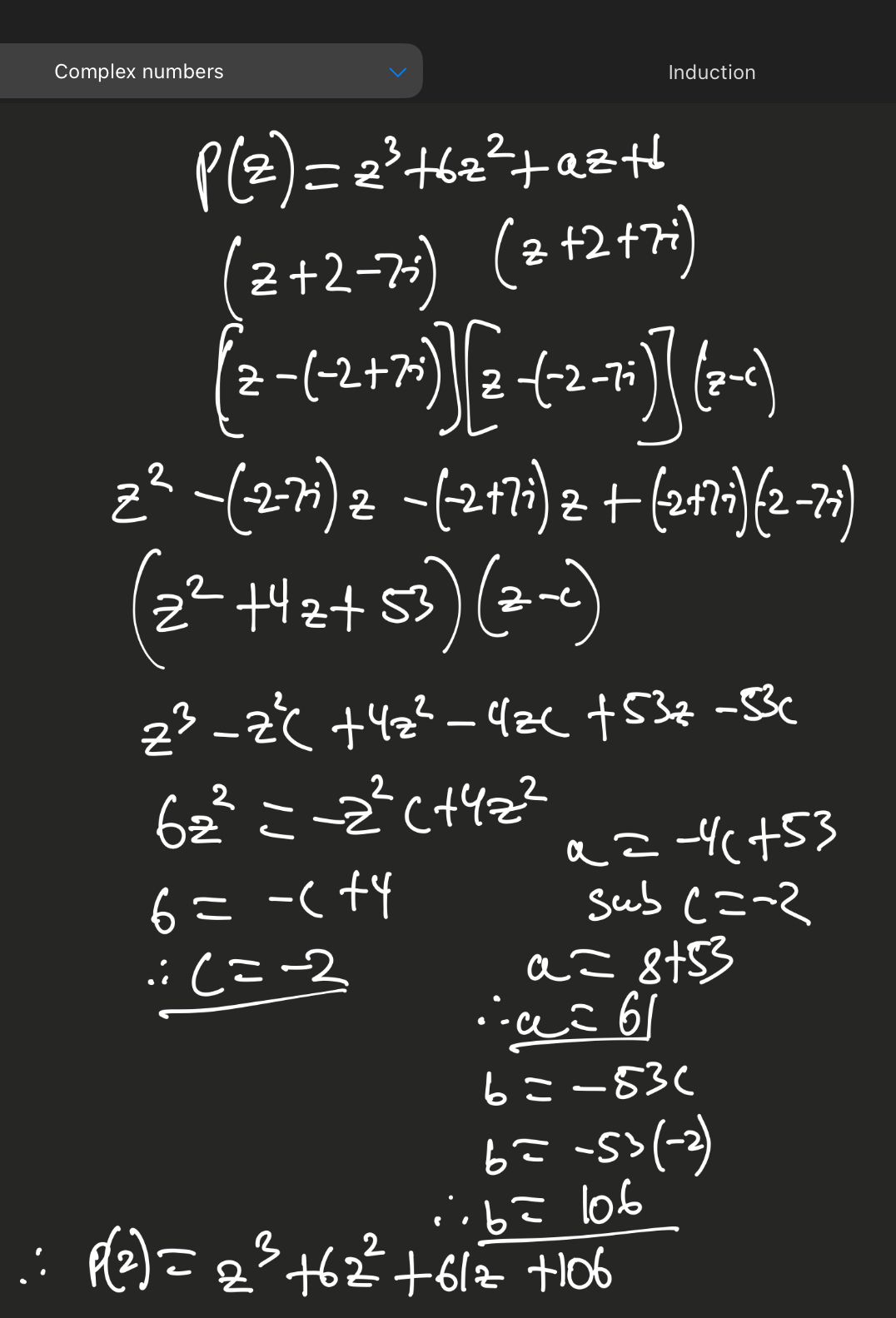
Vector Projection formula

definition of skew lines

only in 3d planes, it is when two lines do not intersect or are parallel with each other

Vector equation of a sphere

equation for leslie matrices

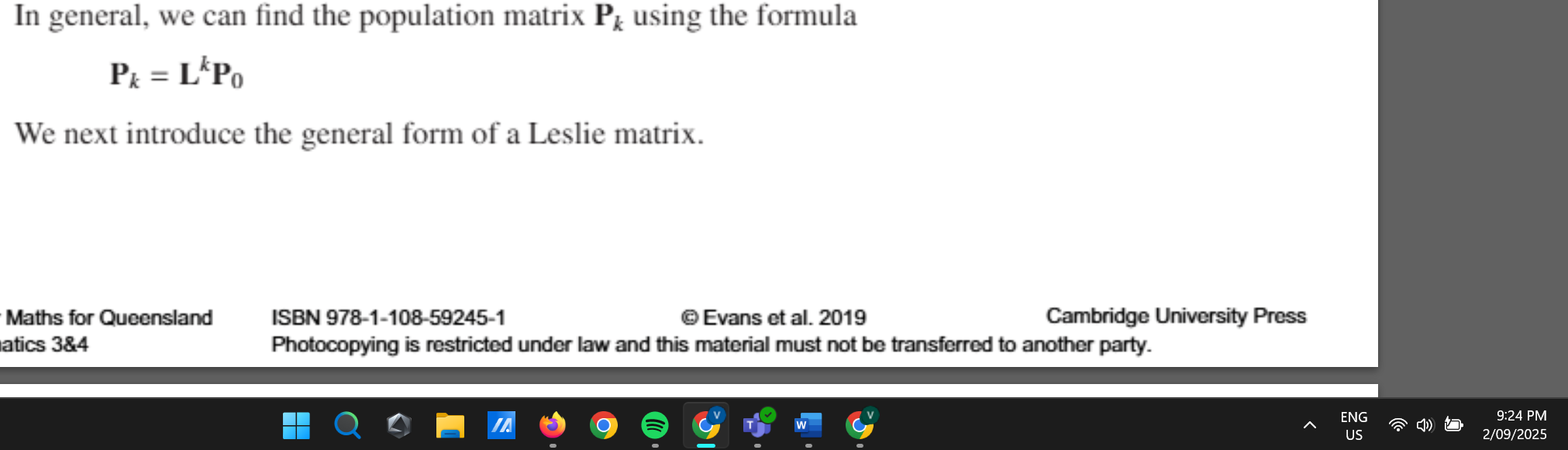
leslie matrix formation

circular motion formulas

for complex numbers arg(z), if the angle is above or below the range -pi to pi then do this

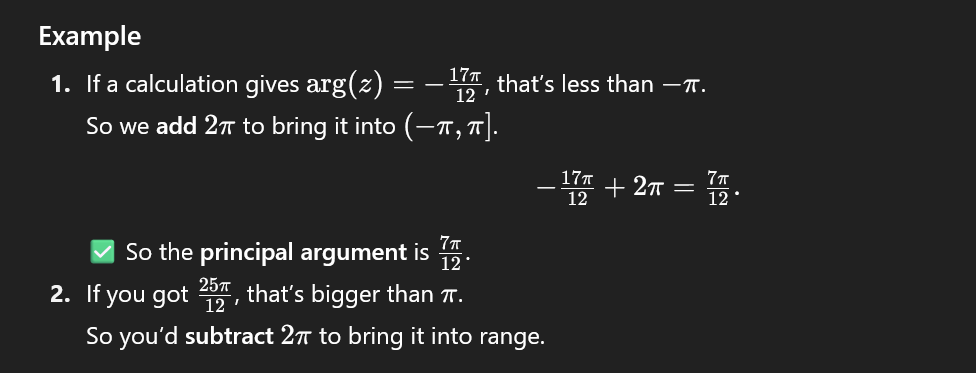
Conditions for the function to be circular motion

Not allowed (if you want pure circular motion)

• Products of trig functions: cos⁡(ωt)sin⁡(ωt)\cos(\omega t)\sin(\omega t)cos(ωt)sin(ωt)

• Squares: cos⁡2(ωt)\cos^2(\omega t)cos2(ωt), sin⁡2(ωt)\sin^2(\omega t)sin2(ωt)

• Different frequencies: one term has cos⁡(ωt)\cos(\omega t)cos(ωt), the other sin⁡(2ωt)\sin(2\omega t)sin(2ωt)

geometric interpretation for a system of linear equations with infinite solutions 

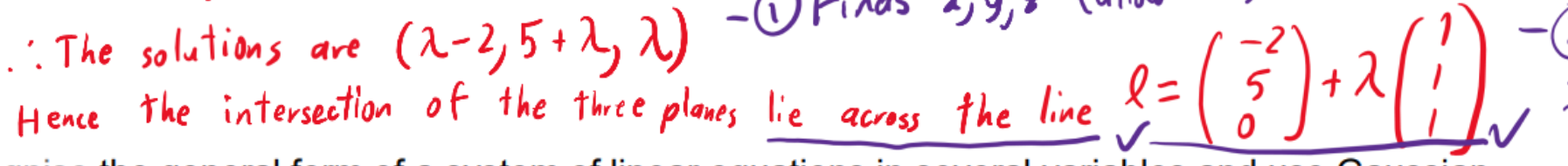
what is T, omega(w), and f actually mean in circular motion

• ω\omegaω tells how fast the angle changes

• T tells how long one circle takes

• f tells how many circles per second happen

in the formula book for sample means standard deviation what does it actually mean

the standard deviation of the sampling distribution of the sample mean.

• If you kept taking lots of different random samples of 15 rats each,

• each sample would have its own sample mean (xˉ\bar{x}xˉ),

• those means wouldn’t all be exactly 65, they’d vary around the true population mean μ\muμ,

• the spread of those sample means is what the SE measures.