MA-105: Module 4 Vocabulary (Probability, Fundamental Counting Principle, Permutations, Combinations)

Probability, Fundamental Counting Principle, Permutations, Combinations

What is the Fundamental Counting Principle?

A strategy used to count the number of possible outcomes in a situation

---

Example: “The model of car you are thinking of buying is available in ten different colors and four different styles. In how many ways can you order the car?”

Answer: 40 (10 times 4)

What is a permutation?

What is a combination?

When is a permutation used?

What is the permutation formula?

P = n! / r!(n - r)!

---

n = number of total objects

r = number of objects selected

Solve this FACTORIAL problem:

In how many distinct ways can the letters of the word TELEVISION be arranged?

There are 10 letters in the word “television”.

There are TWO E’s and TWO I’s

---

10! = 3,628,800

2! (for both the E’s and the I’s) = 2

3,628,800 divided by 2 (for the E’s) = 1,814,400

1,814,400 divided by 2 (again, for the I’s) = 907,200

THUS, The letters of the word TELEVISION can be arranged in 907,200 distinct ways.

How many cards are there in a deck?

52 cards

How do you find the probability of EITHER (one or the other) option being chosen?

(E.g.: Find the probability of drawing either a diamond OR a club card.)

Find the probabilities of selecting each option, and ADD them

---

Example: Probability of drawing a club = 13/52 (52 total cards in a deck, 13 club cards)

Probability of drawing a diamond = 13/52

13/52 + 13/52 = 26/52 —> ½ simplified

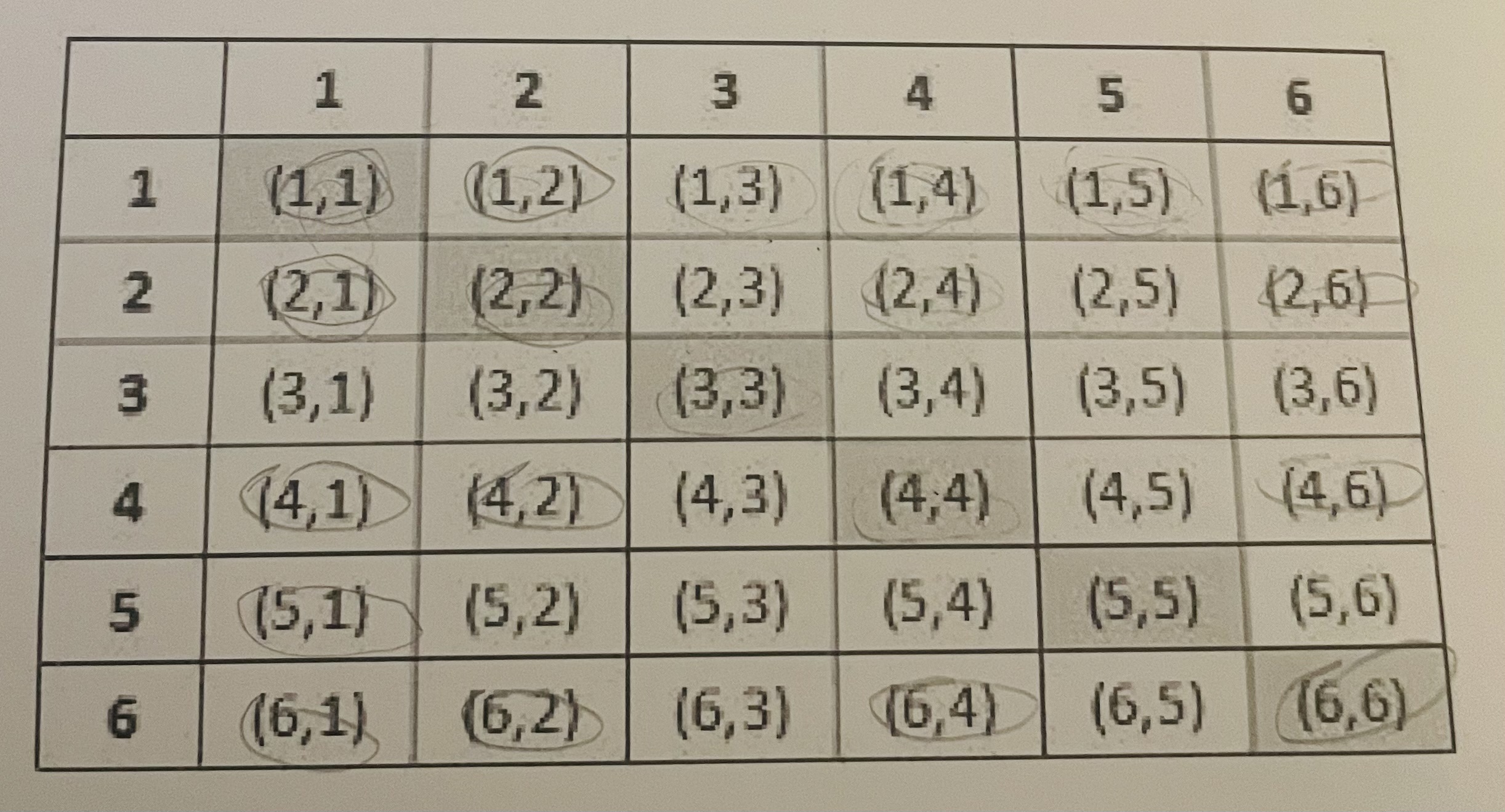
Memorize this! The amount of possible combinations for a single die! :)

What is the meaning of this: ! character?

As in: 5!

This symbol means: “factorial”.

Used to denote an integer and all of the integers below it.

---

Example: 5! means 1 × 2× 3 × 4× 5

When is ! (factorial) used?

Used to find how many ways objects can be arranged in order.

---

Example: Find the number of different finishes for a race with 9 runners.
(Assume no ties occur.)

Solution: 9! (equals 362,880)

Solve this problem when:  b) Repetitions ARE allowed

Problem: How many 10-digit license plates can be made using the digits 0,1,2,3,4,5,6,7,8,9 if an odd digit must be first?

Answer:

An odd number MUST be the first digit: There are FIVE odd numbers in this set.

5 × 10 × 10 × 10 × 10 ×10 × 10 × 10 × 10 × 10

---

*There are 9 spots remaining when an “odd number” is placed first!

There are 10 total digits to choose from, in total.

Remember: Repetitions ARE allowed.

Solve this problem when:  b) Repetitions are NOT allowed

Problem: How many 10-digit license plates can be made using the digits 0,1,2,3,4,5,6,7,8,9 if an odd digit must be first?

An odd number MUST be the first digit: There are FIVE odd numbers in this set.

5 × 9 × 8 × 7 × 6 ×5 × 4 × 3 × 2 × 1

---

*Once 5 is placed first, all of the following spaces denote the number of TOTAL choices available, in DESCENDING order.

In other words, the “tenth place” spot is already taken —> continue to count down from 10.

How many face cards are in a deck?

12 face cards

How many spades are in a deck?

13 spades

How many aces are in a deck?

4 aces

How many king cards are there in a deck?

4 kings

How many queen cards are there in a deck?

4 queens

How many jacks are there in a deck?

4 jacks