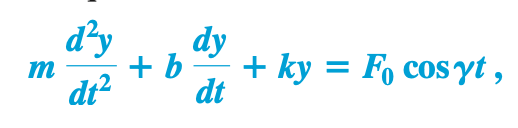C4 - Linear Second-Order Equations

Linear differential equations

Differential equations only including simple functions of x

• No square roots

• No exponentials/ variable powers

• No transcendentals

Homogeneous differential equation

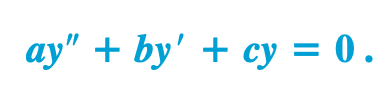
• Simple root:

  • y = e^rt

• Double root:

  • y₁ = e^rt

  • y₂ = te^rt

• Complex root:

  • y = e^rt = e^α[cos(βt) + sin(βt)]

Nonhomogeneous differential equation

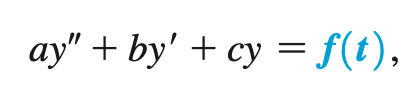
Method of undetermined coefficients

Superposition principle

Existence & uniqueness (homogeneous)

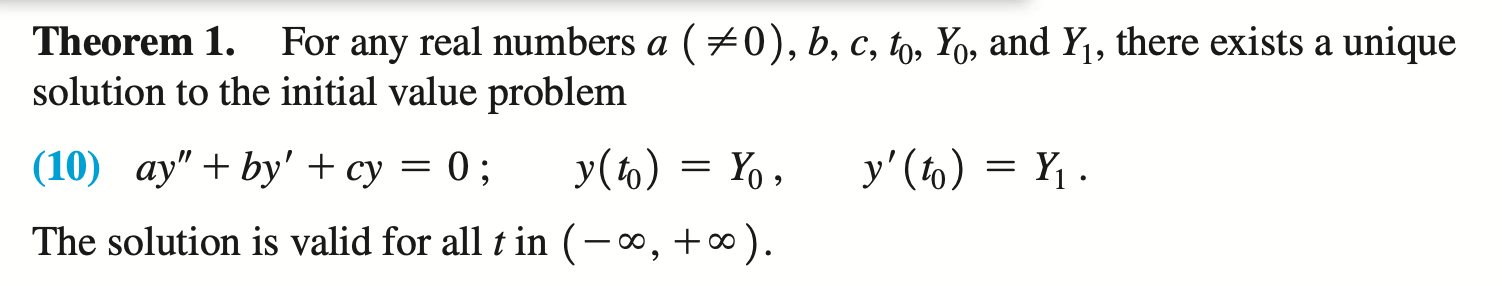
Existence & uniqueness (nonhomogeneous)

Method of variation of parameters

Given ay’’ + by’ + cy = f:

1. Find homogeneous solutions (y₁ & y₂)

2. Substitute, solving for v₁ & v₂:

   1. v₁’y₁ + v₂’y₂ = 0

   2. v₁’y₁’ + v₂’y₂’ = f/a

3. General solution found: y_p = v₁y₁ + v₂y₂

Existence & uniqueness (variable coefficients)

Cauchy-Euler (equidimensional) equation

Solvable variable-coefficient equation

• at²y’’ + bty’ + cy = f

• Characteristic equation: ar² + (b-a)r + c = 0

  • Simple roots: y = t^r

  • Double root:

    • y₁ = t^r

    • y₂ = (t^r)[ln(t)]

  • Complex roots:

    • y₁ = t^αcos[βln(t)]

    • y₂ = t^αsin[βln(t)]

Reduction of order

Mass-spring oscillator equation (full)

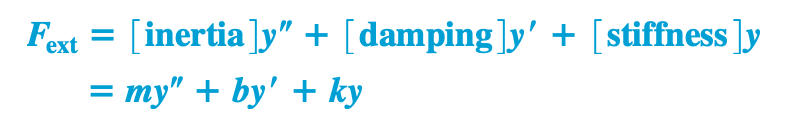
Mass-spring oscillator equation (free, undamped)

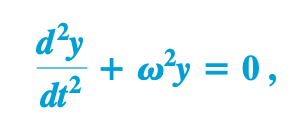
Mass-spring oscillator equation (forced oscillations)