module 7 momentum and collisions

momentum (p→) =

mv→

sum of force in terms of momentum

ΣF→ = dp→/dt

if sum of forces is zero

momentum is conserved, and vice versa

impulse (I→) =

Δp→ = F→_avg * Δt

F→_avg

1/Δt ∫t1 to t2 of F dt

elastic collision

total KE and momentum are conserved

inelastic collision

total KE changes while total momentum is conserved

perfectly inelastic collision

two colliding objects stick together after collision

vf of perfectly inelastic

m1v1 + m2v2 / m1 + m2 (v are vectors!)

elastic collision in 1d relation of velocities before and after

Δvi = -Δvf

v1f in 1d elastic

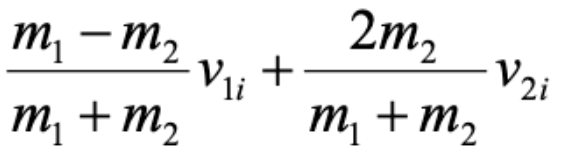
v2f in 1d elastic

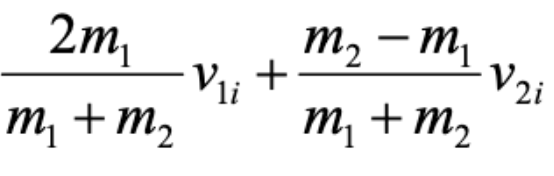
ballistic pendulum

v of projectile = (sum of masses/mass of projectile)√2gh, h is the height that the system rose

glancing elastic collision in 2D components

x: m₁v_1i = m₁v_1fcosθ + m₂v_2fcosφ

y: 0 = m₁v_1fsinθ - m₂v_2fsinφ

when m’s are equal in glancing collision (e.g. billiard balls)

v_1i² = V_1f² + V_2f²

in billiard ball situation, dot product of final velocities is zero, meaning

they are orthogonal

left off on

center of mass and rockets

center of mass for a system of particles

summation of positions x masses / summation of masses

center of masses for extended object

1/M ∫ r→ dm

dm =

density dx dy dz

center of mass of a rod

L/2

center of mass of a right triangle

2/3 from the taller part

mass of a cone

1/3•density•height•area of base

center of mass of cone

3/4 • h

center of mass of a system of particles of combined mass M moves like

particle of mass M would move under influence of F_net external

Ma_cm = 

summation of miai = summation Fi

rocket propulsion

vf - vi = v_eln(mi/mf)