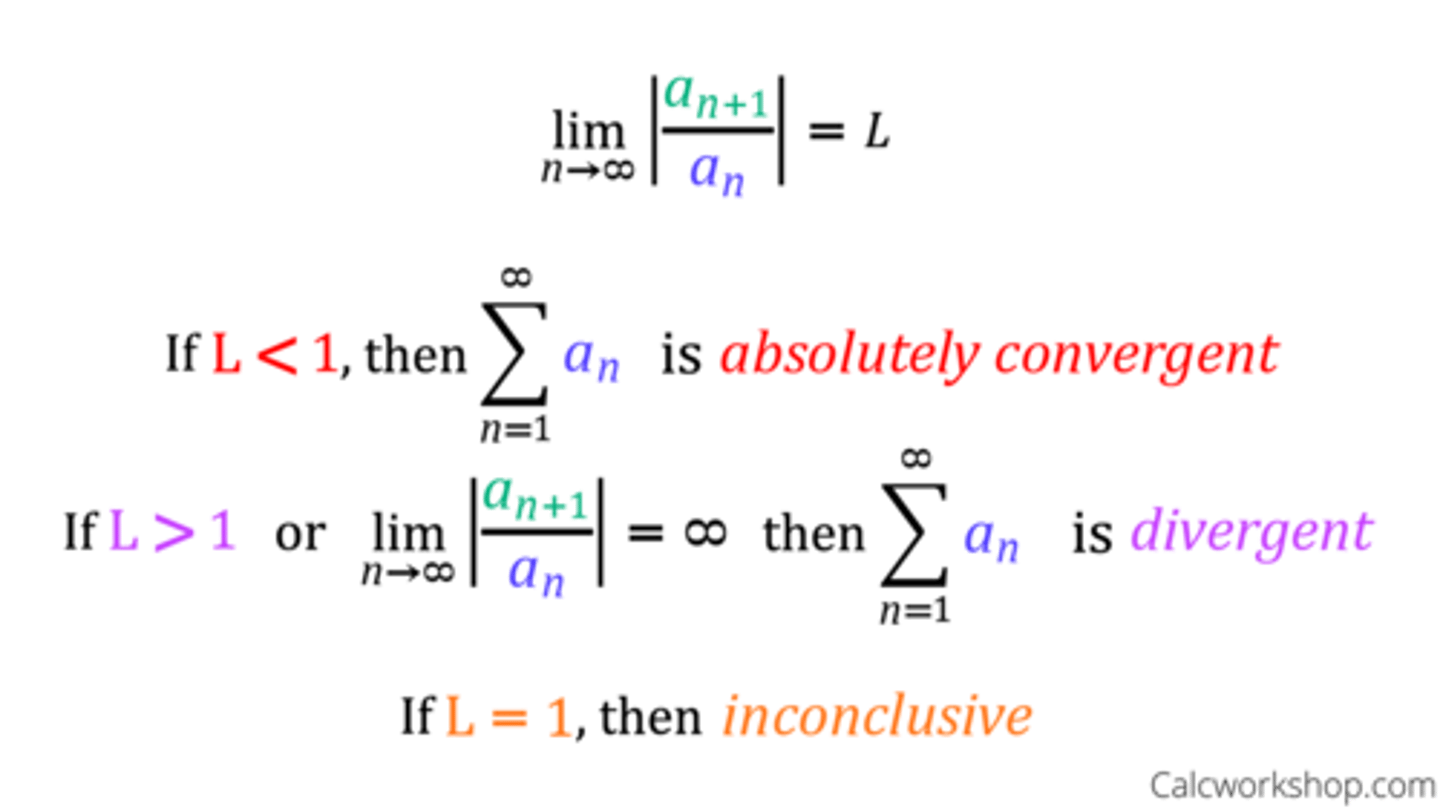Calc BC Convergence Tests
1/14
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
15 Terms
What is the p-series test?
If the series is of the form 1/(n^p),
If p<1, than diverges
If p>1, converges
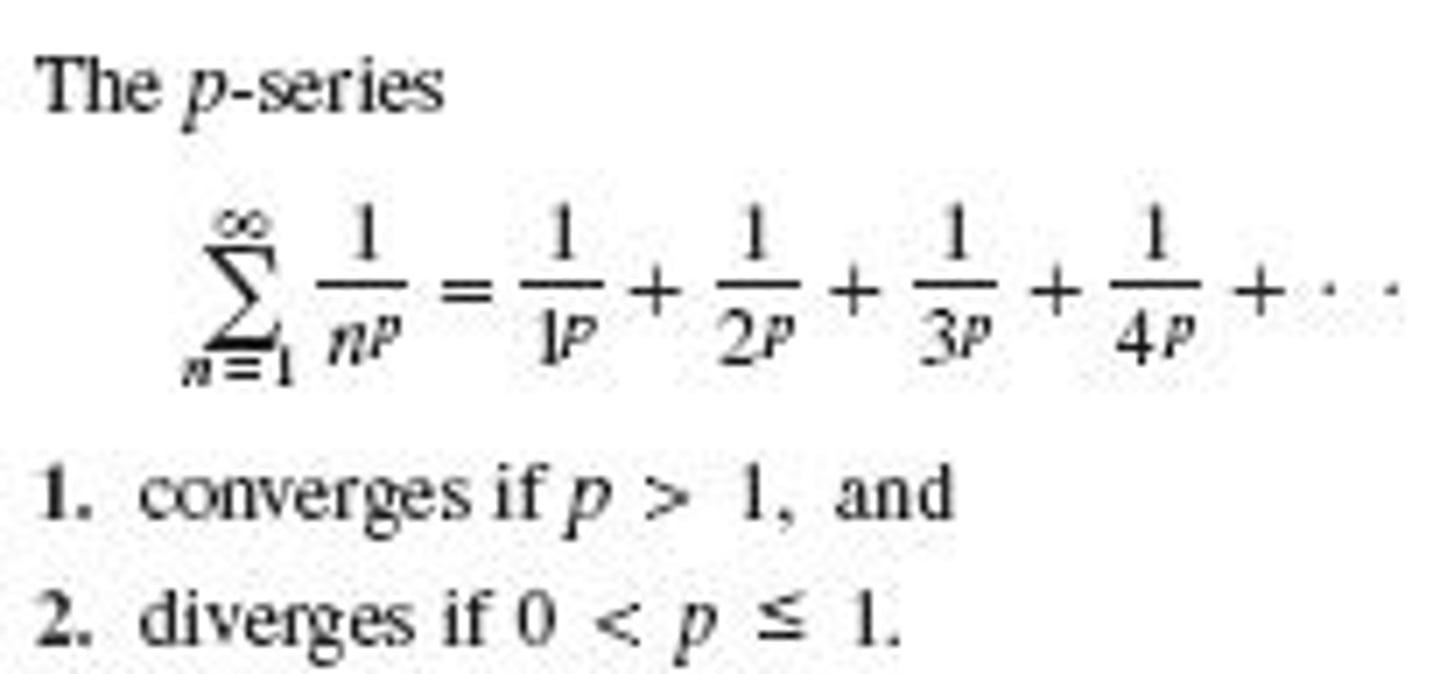
What is the ratio test?
Use the ratio test if have n!
do L=lim l an+1 / anl
n→∞
If lim < 1, absolutely converges
If lim > 1, diverges
If lim = 1, test fails
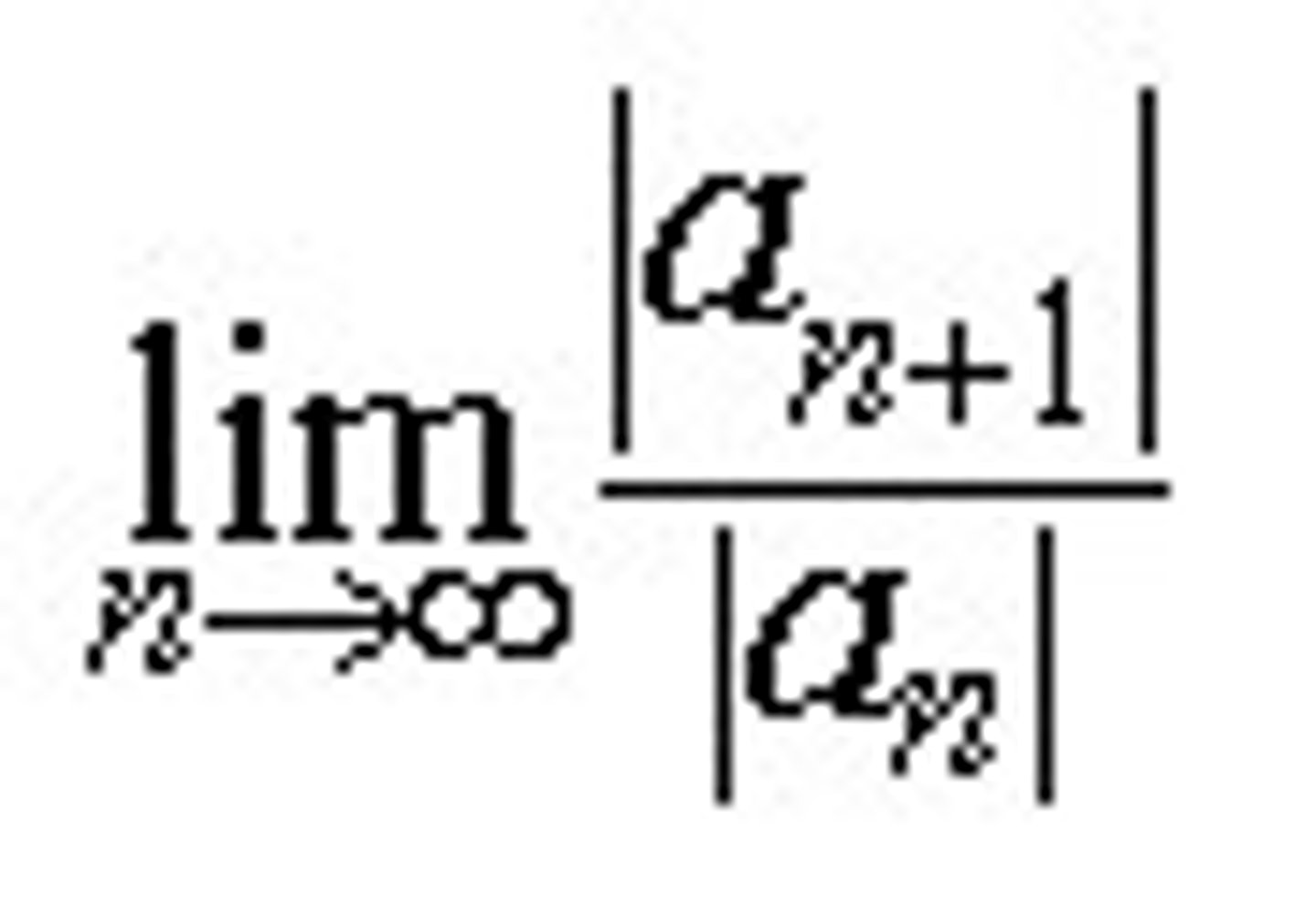
What is the root test?
Take the lim n->inf of the nth root of a[n]
If lim < 1, absolutely converges
If lim > 1, diverges
If lim = 1, test fails
![<p>Take the lim n->inf of the nth root of a[n]</p><p>If lim < 1, absolutely converges</p><p>If lim > 1, diverges</p><p>If lim = 1, test fails</p>](https://knowt-user-attachments.s3.amazonaws.com/0625c2bb-ceb6-4fc9-91d8-ca3afb3abdd5.jpg)
What is the Alternating series test?
Converges if and only if
1) lim an = 0
n→∞
2) an+1≤an

What is the Geometric Series Test?
Converges to S=a/(1-r) if lrl<1
Diverges if lrl≥1
If the series is of the form r^n
Plug in 1st # to get first term.
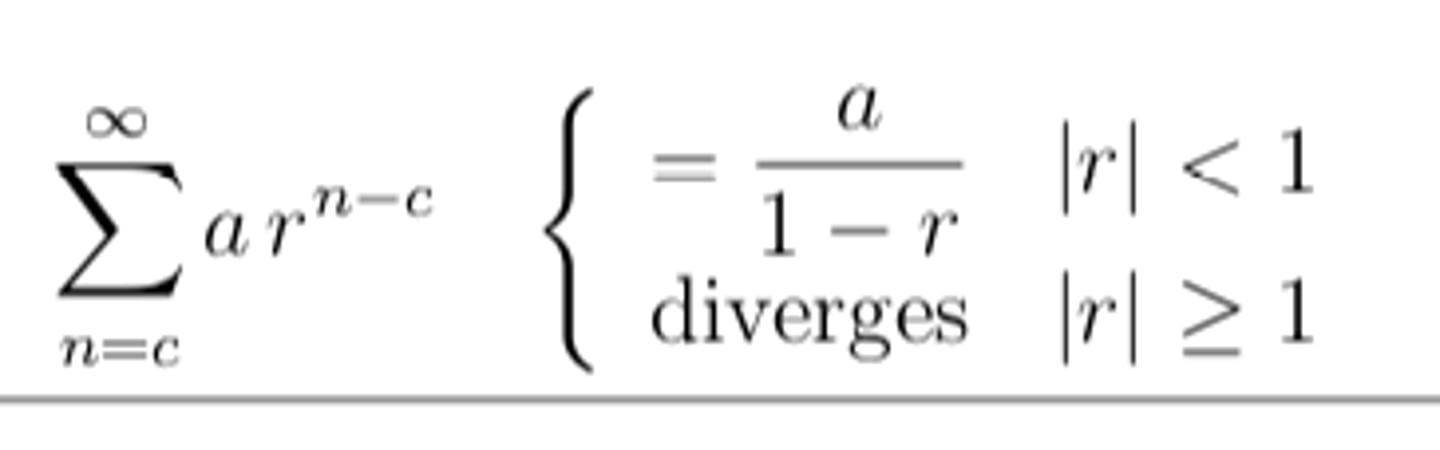
What must the series do in order to use the integral test?
1. Continuous
2. Positive
3. Decreasing
What is the integral test?
If the definite integral from some a to infinity of the series converges, than the series converges.
If the integral diverges, than the series diverges.
*just switch the sigma with an integral
NOTE: Very often this involves u sub, actually almost always Remember LIATE
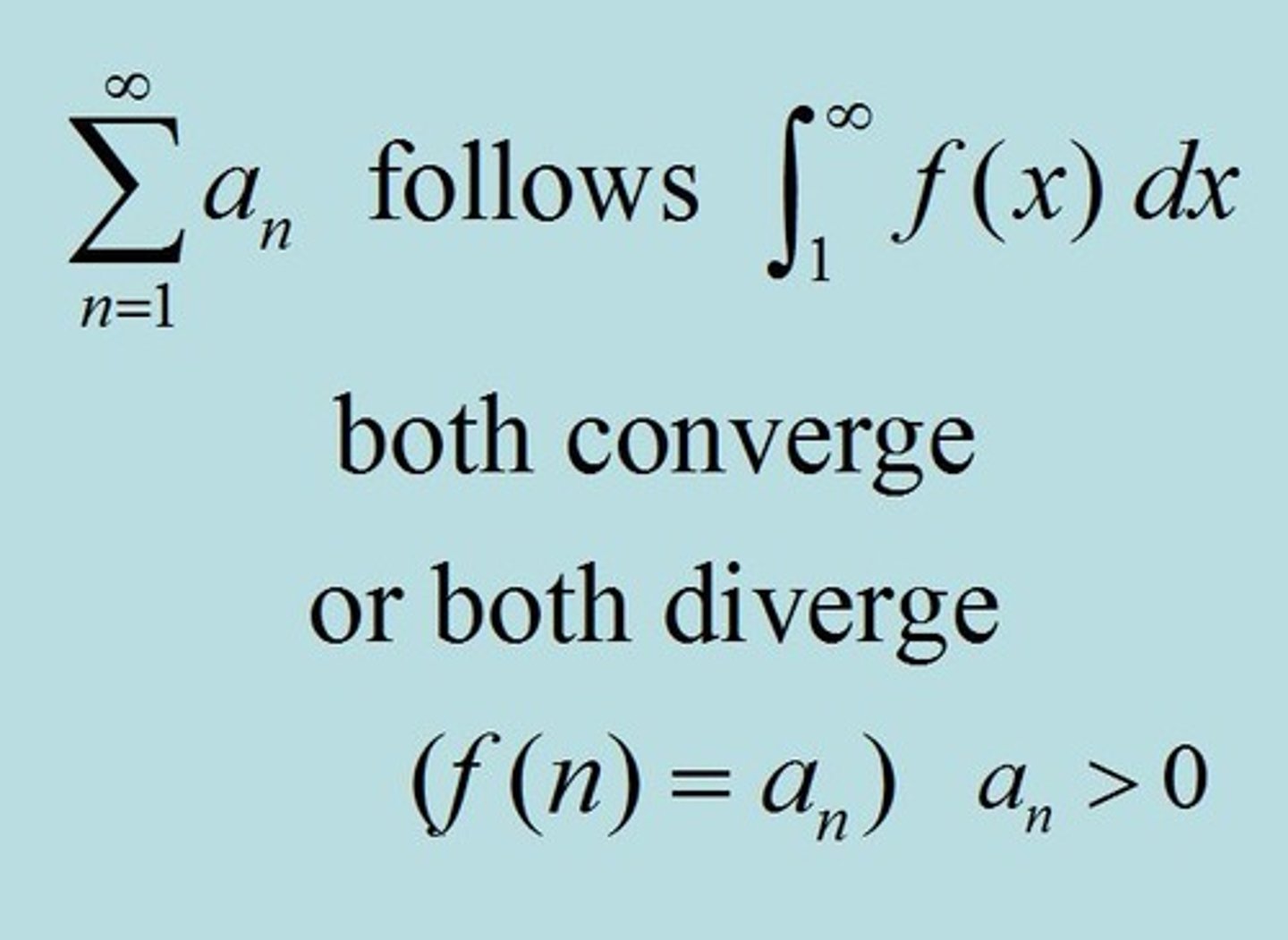
What is the direct comparison test to converge?
If a[n] > b[n], and if a[n] converges, than b[n] must also converge.
![<p>If a[n] > b[n], and if a[n] converges, than b[n] must also converge.</p>](https://knowt-user-attachments.s3.amazonaws.com/afdca3c7-63f6-4ad2-8485-84eb10165b69.jpg)
What is the direct comparison test to diverge?
If a[n] < b[n], and if a[n] diverges, than b[n] must also diverge.
![<p>If a[n] < b[n], and if a[n] diverges, than b[n] must also diverge.</p>](https://knowt-user-attachments.s3.amazonaws.com/6b63d576-8cb2-414a-abf4-457e21272f83.jpg)
What is the limit comparison test?
Take the lim n->inf of a[n]/b[n]
If the lim is positive and finite, then both a[n] and b[n] either converge or diverge.
![<p>Take the lim n->inf of a[n]/b[n]</p><p>If the lim is positive and finite, then both a[n] and b[n] either converge or diverge.</p>](https://knowt-user-attachments.s3.amazonaws.com/ed7b9251-292d-40b0-ad95-c90960070e7e.jpg)
What is the absolute convergence test?
If Ia[n]I converges, than a[n] absolutely converges
![<p>If Ia[n]I converges, than a[n] absolutely converges</p>](https://knowt-user-attachments.s3.amazonaws.com/f0616c58-e2d7-45e9-80f3-ecddf535c1e3.jpg)
nth term test (divergence test)
If the lim n -> inf of a[n] = anything but 0, it for sure diverges.
But if it does = 0, than the test fails.
hint: if the top power is teh same or greater than the bottome power than series diverges!
![<p>If the lim n -> inf of a[n] = anything but 0, it for sure diverges.</p><p>But if it does = 0, than the test fails.</p><p>hint: if the top power is teh same or greater than the bottome power than series diverges!</p>](https://knowt-user-attachments.s3.amazonaws.com/f132dfb9-23cb-4f1b-a947-8b7b339556cc.jpg)
Telescoping Series Test
factorable polynomial-do partial fractions and then usually BUT NOT ALWAYS have to break into two separate sigma notations
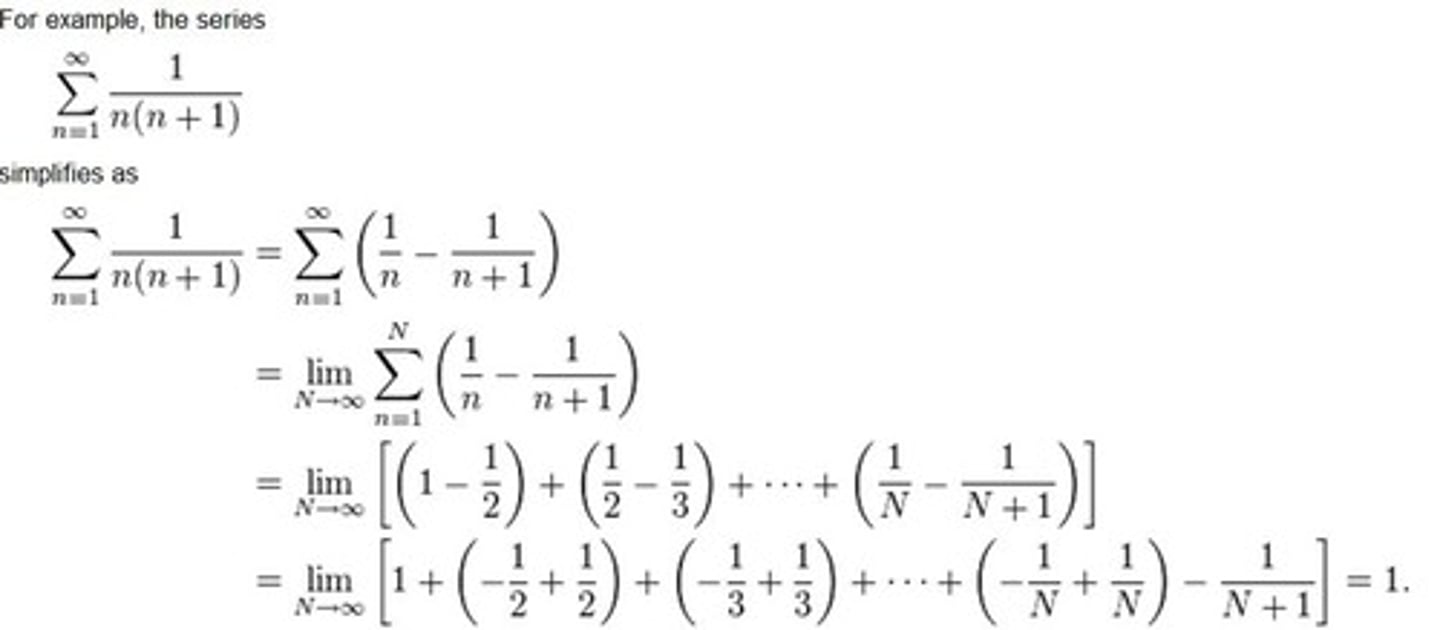
Absolute and Conditional Convergence
A series ∑an is called absolutely convergent if ∑|an|∑|an| is convergent. If ∑an is convergent and ∑|an| is divergent we call the series conditionally convergent.
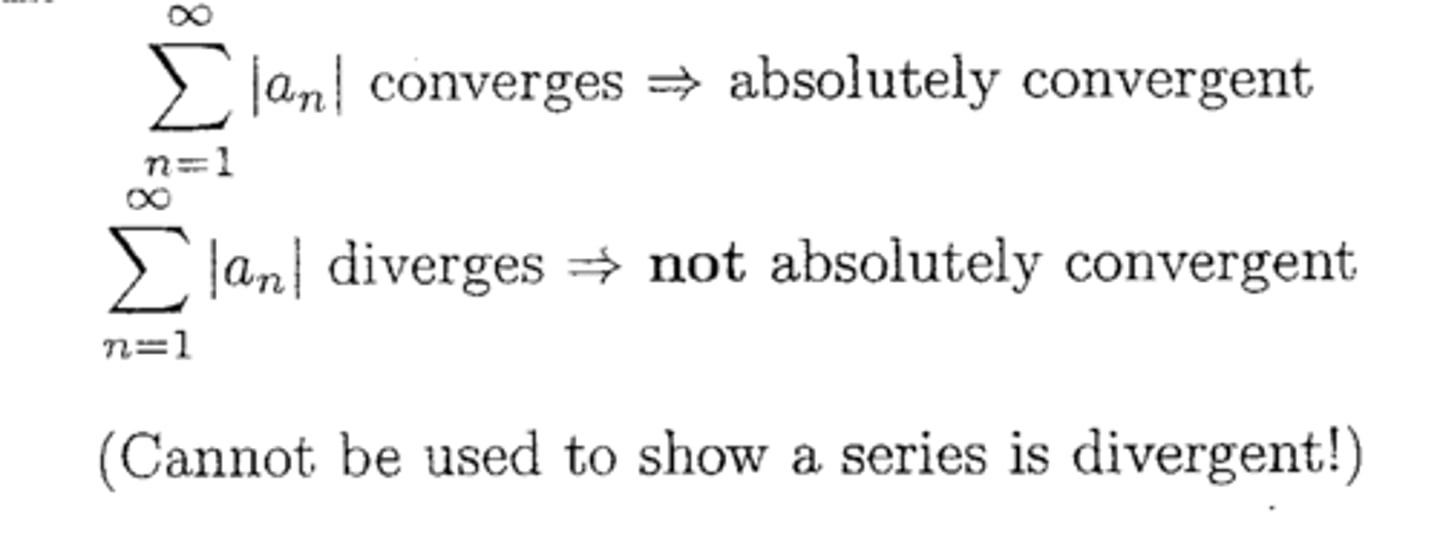
Ratio Test for Absolute Convergence
Take the absolute value and do the ratio test.
do L=lim l an+1 / anl
n→∞
If lim < 1, absolutely converges
If lim > 1, diverges
If lim = 1, test fails