Electromagnetism (Electric Fields) - Model Answers

1. Explain how an insulating object can become charged.

• Electrons can be transferred from one object to another.

• Via friction.

• The object gaining electrons becomes negatively charged.

2. Describe what is meant by an electric field.

• A region where a charged particle experiences a force.

3. Define electric field strength.

• The force per unit positive charge.

4. State the equation for electric field strength.

• E = F/q_source

• Where E is the electric field stregth.

• F is the electrostatic force.

• q is the charge of the charge placed within the field.

5. State whether the following are vectors or scalars.

   Coulomb force

   Electric field strength

• Coulomb force - Vector

• Electric field strength - Vector

6. Describe the direction of electric field lines.

• Electric field lines point in the direction that a positive point charge would experience a force. (*from +ve to -ve).

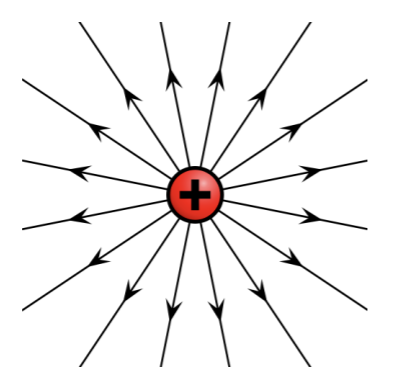
7. Draw the electric field around a positive point charge.

• Radial field.

• Electric field strength decreases with distance from charge (field lnes become further apart).

• Field lines meet charge at right angles to its surface.

• Arrows point in the direction that a positive point charge would experience a force (away from +).

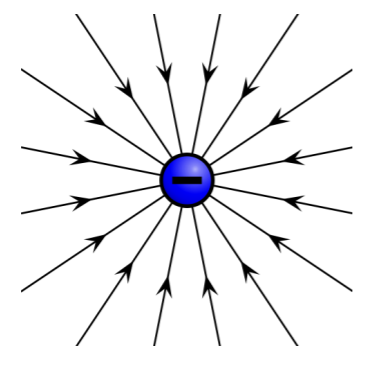
8. Draw the electric field around a negative point charge.

• Radial field.

• Electric field strength decreases with distance from charge (field lnes become further apart).

• Field lines meet charge at right angles to its surface.

• Arrows point in the direction that a positive point charge would experience a force (towards -).

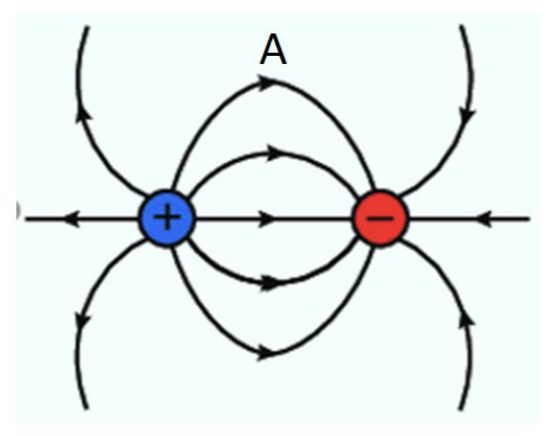
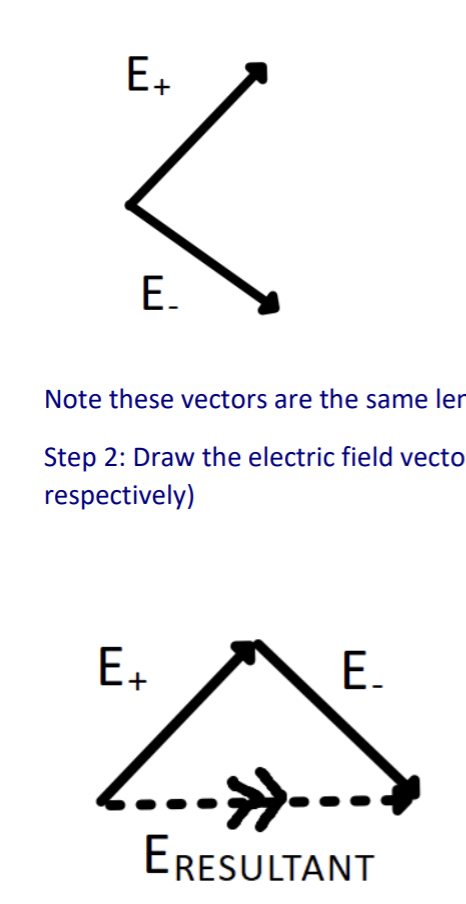
9. Show how the electric field vector at A has been constructed.

• Step 1 - Draw the electric field vectors sue to the positive and negative charge (E₊ and E_- respectively).

• *Note the vectors are the same length because point A is the same distance from each charge.

• Step 2 - Draw the electric field vectors due to the positive and negative charges (E₊ and E_- respectively).

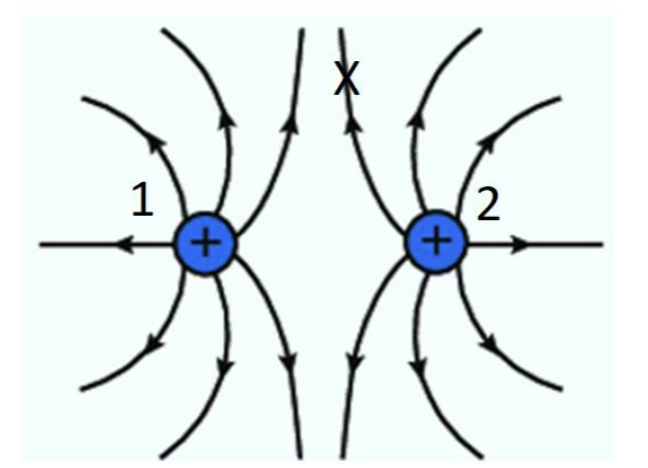
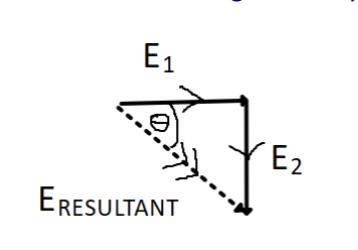
10. Show how the electric field at X has been constructed.

• Step 1 - Identify the electric field vectors due to charge 1 and charge 2.

• *Note that E1 is shorter in length than E2, as the point we are considering is further from charge 1 than charge 2.

• Step 2: Vector diagram.

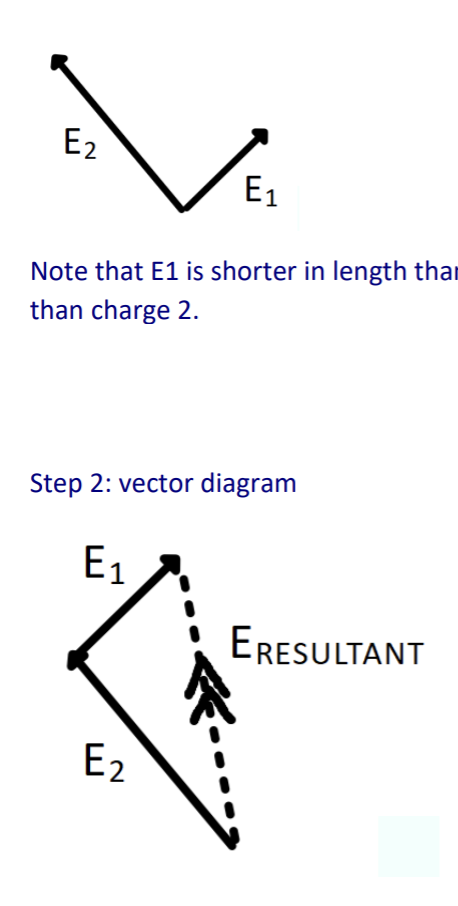
11. Draw the electric field lines between a positive point charge and nagative place.

• Charges coming in all directions.

12. Define unifrom electric field.

A field in which the electric field strength is constant everywhere.

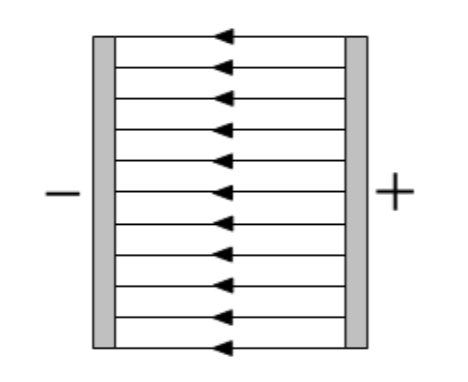
13. Draw the electric field between two infinite parallel plates.

Key points to note:

• Arrows from + to - (as this is the direction of a +charge would experience.

• Field lines equidistant (as the electric field strength is presented by the clossness of field lines, and this is constant).

• Field lines meet plates perpendicular to the plate.

14. State the equation for the electric field in a uniform field.

• E = V/d.

• Where E was the electric field strength.

• V is the potential difference across two plates.,

• d is the seperation between the two parallel field.

15. Derive the expression for the charge q on an oil drop that is held stationary within an uniform electric field.

• W = F_e

• mg = Eq

• mg = Vq/d

• q = mgd/V

• q = 4/3 πr³ρgd / V

16. Explain how Millikan dertermined the radius of the oil drop in his experiment.

• Let the oil drop fall through air at terminal velocity.

• Use v = s/t to determine the terminal velocity.

• At terminal veocity, W = F (Stroke’s drag force).

• mg = 6πrηv

• 4/3 πr³ρg = 6πrηv

• r² = 9/2 ηv / ρg

17. Calculate the speed of an electron that has been accelerated by a pd of 500V. Electron charge = 1.6 × 10^-19 C, electron mass = 9.11 × 10^-31kg.

• Work done = kinetic energy gained.

• Vq = ½ mv²

• 500 × 1.6 ×10^-19 = ½ x 9.11 × 10^-31 v²

• v = 1.3 × 10⁷ ms^-1.

18. Define thermionic emission.

Release of electrons from the surface of a metal due to heating.

19. The diagram below show the structure of a linear accelerator (LINAC).

    • Explain what the LINAC does to the motion of charged particles as they pass from one drift tube to another. [3]

    • Describe the motion of the charged particle inside the drift tube. [3]

    • Explain why the power supply should be alternating. [1]

    • Describe what the frequency of the alternating supply should be. [2]

    • Explain why the length of the tube increases. [3]

• The electric field acts in the gaps between the drift tubes [1], this causes a resultant force on the charged particle towards the target [1]. Due to Newton’s second law, this causes an acceleration to the right in between the tubes [1].

• Inside the drift tube, there is no electric field [1], so the charge experiences no resultant force [1], and due to Newton’s first law, it moves with a constant velocity [1].

• Power supply alternates to ensure the potential of each tube alternates. This ensures the electric field continues to accelerate the charge between tubes through appluing a force towards the target at each gap.

• The frequency should be equal to 1/(2 time in tube), so that the potential of each tube changes just as the charge arrives at the end of the tube [1]. As the time in tube is low, the alternating supply frequency should be high.

• As the charged particles accelerates, its speed increases [1]. To ensure it spends the same time in each tube [1], the tube length must increase by the same factor that the speed has, as time distance / speed.

20. An electron beam enters a uniform electric field consisting of two plates separated by 10cm with a potential difference of 300V. The electron beam has horizontal velocity of 2.9 × 10⁷ ms^-1. Calculate the vertical deflection of the electron beam after it has travelled 20cm.

Horizontally there is no acceleration. So:

• s = ut

• 0.2 = 2.9 × 10⁷t

• t = 6.8965 × 10^-9 s

Vertical acceleration:

• F = Eq = Vq/d = 300 × 1.6 × 10⁼¹⁹ / 0.1 = 4.8 × 10^-16N.

• F = ma

• 4.8 × 10^-16 = 9.11 × 10^-31 x a

• a = = 6.8965 × 10^-9 s

Vertical deflection:

• s = ?

• u = 0 ms^-1

• v =

• a = 5.2 × 10¹⁴ ms^-1

• t = 6.8965 × 10^-9 s

• s = ut + ½ at²

• ½ at² = ½ x 6.8965 × 10^-9 s x (6.8965 × 10^-9 s)²

• = 0.0128 m

• = 1.28 cm

21. State Coulomb’s Law.

• F = kq₁q₂/ r²

• Where F is the electrostatic force

• k is Coulomb’s constant = 8.99 × 10⁹ Nm²C^-2

• r is the sepeartion between the centres of the charges

22. Derive the base unit for k.

• k = Fr² / q₁q₂

• [k] = [F] [r]² / [Q]² = Nm²C^-2

• Base units are: m, s, A, kg

• So N = kgms^-2 and C= As

• [k] = kgms^-2m²A^-2s^-2

• = kgm³s^-4A^-2

23. Describe the relationship between force and separation between charges.

The force is inversely proportional to the square of the separation (inverse square law).

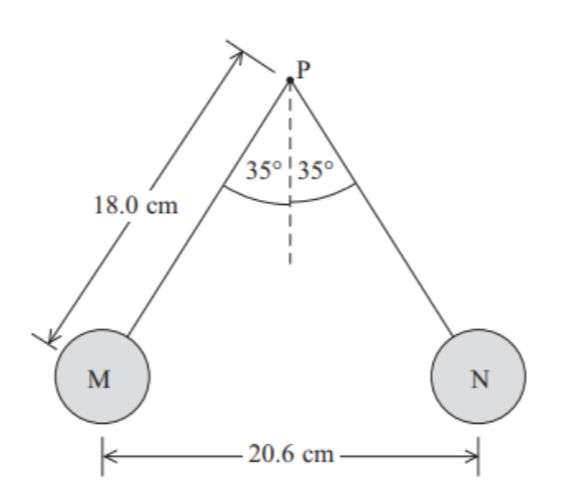
24. Two identical table tennis balls, M and N, are attached to non-conducting threads and suspended from a point P. The balls are each given the same positive charge and they hang as shown in the diagram. The mass of each ball is 2.7g.

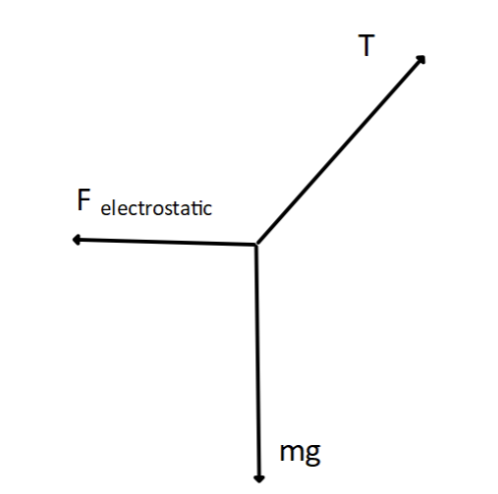
a) Draw a force arrow diagram for charge M.

b) Calculate the charge on each of the charges.

a) Tension in the string, repulsive electrostatic force, weight (mg)

b)

• Resolving forces vertically:

• T_vertical = mg

• T cos35 = 2.7 ×10^-3 × 9.81 = 0.026487

• T = 0.0323 N

• Resolving forces horizontally:

• T_horizontal = F_{electrostatic} = kq₁q₂ / r²

• As each charge has the same charge, q₁ = q₂ and:

• T_horizontal = F_{electrostatic} = kq² / r²

• 0.0323 sin35 = 8.99 × 10⁹ x q² / (20.6 × 10^-2)²

• Q = 2.957 × 10^-7 C = 3.0 × 10^-7 C

25. Derive the expression for the electric field strength in a radial field.

• F = kq₁q₂ / r²

• E = F/q (from the definition of field strength)

• E = kq₁q₂ / r²q

• E = kq / r²

• Where k is Coulomb’s constant, q is the charge creating the field, r is the distance from the centre of the charge q.

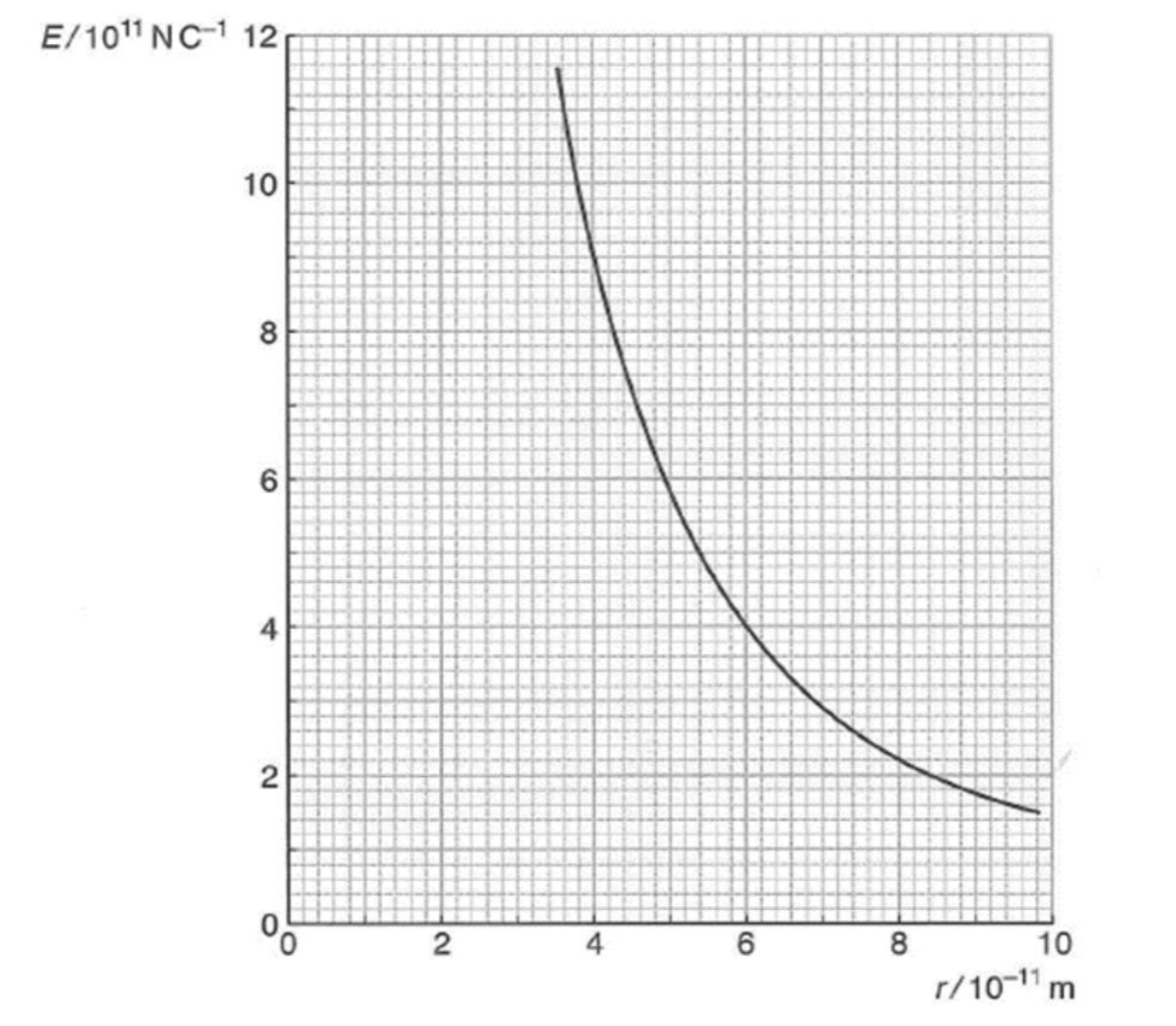
26. Prove the relationship between electric field strength and separation, as shown in this graph, obeys the inverse square law.

• If E and r follows the inverse square law, then Er² should be a constant as E = constant / r²

• E₁r_1² = 11 ×10¹¹ x (3.6 ×10^-11)² = 1.43 ×10^-9 NC^-1m²

• E₂r_2² = 4 ×10¹¹ x (6.0 ×10^-11)² = 1.44 ×10^-9 NC^-1m²

• E₃r_3² = 2 ×10¹¹ x (8.4 ×10^-11)² = 1.41 ×10^-9 NC^-1m²

• Er² is a constant to 2sf, hence E and r follow the inverse square law.

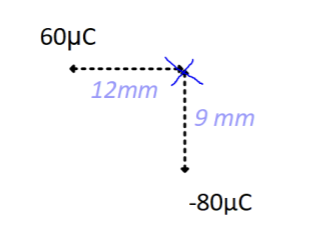
27. Determine the resultant electric field strength at position X.

• Let the 60μC charge be Q1 and the -80μC charge be Q2.

• E₁ = kQ₁/ r_1² = 8.99 ×10⁹ × 60 ×10^-6 / (12 ×10^-3)² = 3.75 ×10⁹ NC^-1

• E₂ = kQ₂/ r_2² = 8.99 ×10⁹ × 80 ×10^-6 / (9 ×10^-3)² = 8.88 ×10⁹ NC^-1 (ignore sign)

• Magnitude of resultant (use Pythagoras):

• E_total = √(3.75 ×10⁹)² + (8.88 ×10⁹)² = 9.64 ×10⁹ NC^-1

• Direction (use trigonometry):

• θ = tan^-1 (8.88 ×10⁹ / 3.75 ×10⁹ )

• = 67.1 degrees below horizontal

28. Define electric potential.

The work done per unit positive charge, in bringing a charge from infinity to a point within the field.

29. Explain why the electric potential is positive for positive charges and negative for negative charges.

• In bringing a positive test charge from infinity to a point within the field around a positive charge, work has to be done against the field.

• This is because the test charge would experience a repulsive electrostatic force in the opposite direction to its displacement.

• So the test charge would gain electrical potential energy as it moves closer to the field creating positive charge (transferring it from kinetic energy).

• Whereas when a positive test charge is brought closer to a negative field creating charge, the test charge would experience an attractive electrostatic force towards the negtive field creator.

• Therefore work would be done by the field.

• The charge’s electrical potential energy would decrease (it would be transferred into kinetic energy) as it gets closer to the negative charge.

30. Sketch a graph of potential against separation from

    a) a positive charge

    b) a negative charge

Inversely proportional graph for positive region - Positive charge

Reflected in x axis - Negative charge

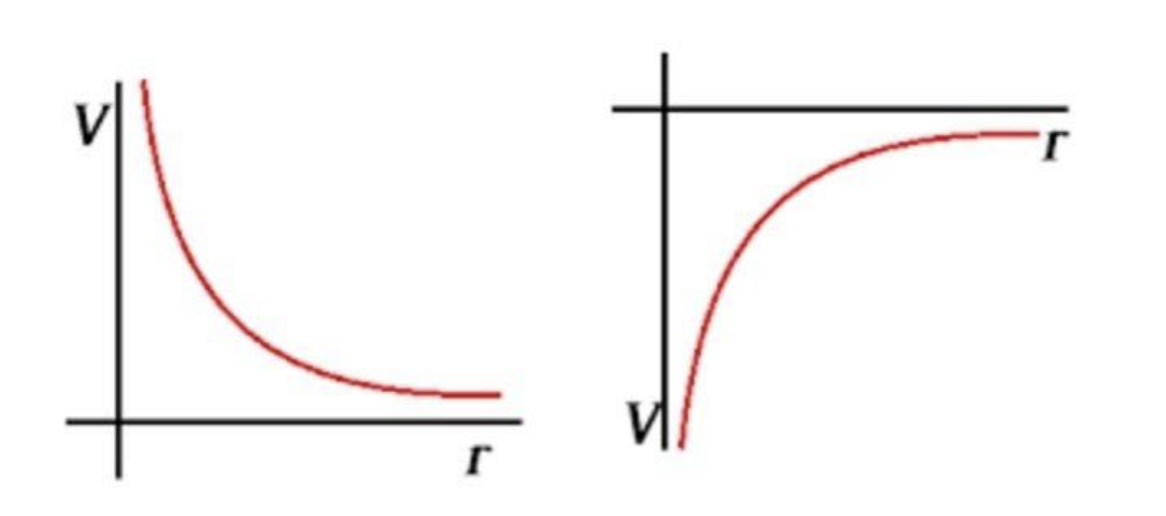
31. Describe the relationship between electric potential, V and seperation, r.

• Potential and separation are inversely proportional.

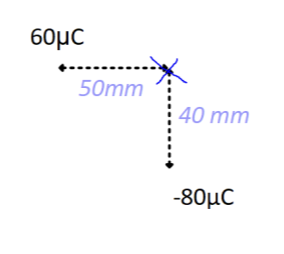
32. Determine the potential at position X due to charges Q1 and Q2.

• V_total = V₁ + V₂

• Let the 60μC charge be Q1 and the -80μC charge be Q2.

• V₁ = kQ₁/ r₁ = 8.99 ×10⁹ × 60 ×10^-6 / 50 ×10^-3 = 10,788,000 V

• V₂ = kQ₂/ r₂ = - 8.99 ×10⁹ × 80 ×10^-6 / 40 ×10^-3 = - 17,980,000 V (KEEP SIGN)

• V_total = V₁ + V₂ = -7,192,000 = 7.192 ×10⁶ V

33. State the equation showing the relationship between electric potential and field strength.

• E = -∆V / ∆r

• E is the electric field strength

• ∆V is the change in potential for a charge, in distance ∆r

34. David Blaine wore a metal suit and was placed in a room with a charged sphere that cuased ionisation at 1m. A scientist claims that David Blaine is completely safe inside the metal cage. Comment on this suggestion. [4 marks].

• There is no potential difference across the cage or his body.

• Electric field strength inside the cage is zero (it is a Faraday Cage).

• This is because there is no potential gradient.

• Current conducts only on the surface of the cage - not inside.

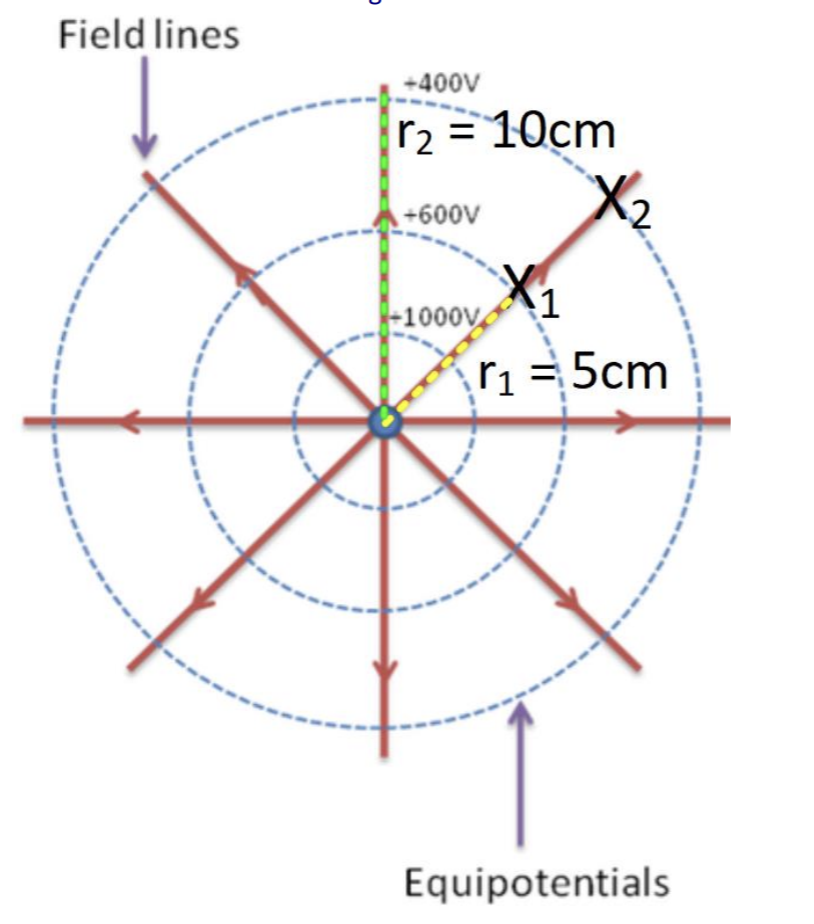
35. Determine the electric field strength between X1 and X2.

E = ∆V/ ∆r = (600 - 400)/ (10 - 5) x10^-2 = 4000 Vm^-1

36. Explain how to determine the electric field strength from a graph of potential against separation.

• Electric field strength is the nagtive gradient of a potential, distance graph.

• If the potential, distance graph is a curve, then the tangent at a point should be drawn and the gradient of this should be found.

37. Calculate the minimum separation between an alpha particle and a gold nucleus if the alpha particle is fired with an energy of 10MeV. The gold nucleus has an atomic number of 79.

• KE of alpha particle = 10 × 10⁶ × 1.6 × 10^-19 J = 1.6 ×10^-12 J

• Decrease in KE of alpha = increase in EPE of alpha

• 1.6 ×10^-12 = Δ Vq

• where q is the charge of the alpha particle, q = 2 × 1.6 × 10^-19 = 3.2 × 10^-19C (as the alpha particle contains two protons)

• ΔV = ΔV₂ - V₁, where V₂ is the final potential (when stationary at the closest point) and V₁ is the initial potential.

• Assuming the alpha particle starts at infinity V₁ = 0V

• Taking the minimum distance of the closest appraoch to be r.

• V₂ = kQ/r where Q is the charge on the gold nucleus (field creator).

• Q = 79 x 1.6 × 10^-19 = 1.264 × 10^-17 C (as the gold nuclus contains 79 protons)

• So:

• 1.6 × 10^-12 = kQq/r (combining the equations together)

• 1.6 × 10^-12 = (8.99 × 10⁹ × 1.264 × 10^-17 x 3.2 × 10^-19) / r

• r = 2.27 × 10^-14m