Micro T1 Game theory

simultaneous game notation

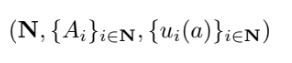
nash equilibrium verbal definition and in terms of utility

an action profile in which all players are simultaneously making optimal choices (playing mutual best responses) – no reason to deviate

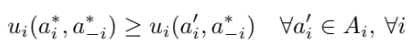
best response in terms of utility

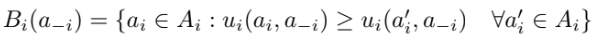
limitations of NE

• multiple or no NE may exist

• requires everyone to play optimally and correctly anticipate what the other will do

• does not consider cooperation

weakly dominantated action

not playing ai is at least as good as ai in all cases and better than ai in one case

dominant action implication for NE

strictly dominant, unique BR thus unique NE

strictly dominated, not a BR thus never played in NE

weakly dominated, can be a BR

iterated deletion, what to delete, outcome

delete strictly dominated actions

if it has a unique prediction it is “dominance solvable”

Baress’ paradox

building a new road can make journey times longer in simultaneous move model

Linear Cournot

choose q to produce

higher q lower price

find monopoly quantities (q_j =0) to draw graph

sub in mirrored quantity produced for other firm

for large number of firms assume we have a symmetric solution qi=q

FOC assumptions

continuous and differentiable

interior solution

concave for max

von Neumann Morgenstern utility function

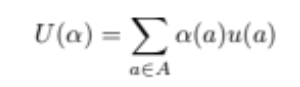
General property of MSNE

Must be indifferent about everything you mix over with positive probability ( if not indifferent would always play one and we would have pure strategy)

issues with mixed strategies

people must randomise even though they would be just as good off playing pure strategy

cant really be truly random

existence of MSNE

Brouwer’s fixed point theorem: Every continuous function from a compact, convex set to itself has at least one fixed point.

dominance in mixed strategies

risk dominant equilibrium

requires smaller % to switch to make it into a PSNE

mixed strategy vs behavioural strategy

mixed strategy mixes with probability over strategies

behavioural strategy mixes with probability over actions at each specific node

both give the same NE

Existence of SPNE

Zermelo’s Theorem: In all finite games of perfect information, there always exists a (pure strategy) SPNE

information sets

strategy defined for each information set

if nature is observed it counts as an information set

count number of lines and nodes that dont have lines

identifying subgames in game tree

can only start at singleton information set, whole game is also a subgame but not a “proper” one

repeated game payoff theory