APEX Arithmetic Practice Problems

What is 12/60 converted to a percentage?

The fraction 12/60 can be reduced to 1/5, in lowest terms. First, it must be converted to a decimal. Dividing 1 by 5 results in 0.2. Then, to convert to a percentage, move the decimal point two units to the right and add the percentage symbol. The result is 20%.

What is the correct decimal form of the fraction 14/33 rounded to the nearest hundredth place?

If a calculator is used, divide 33 into 14 and keep two decimal places. If a calculator is not used, multiply both the numerator and denominator times 3. This results in the fraction 43/99 and hence an approximate decimal of 0.42.

What represents the correct sum of 14/15 and 2/5?

Common denominators must be used. The LCD is 15, and 2/5 = 6/15. Therefore, 14/15 + 5/15 = 20/15, and in lowest terms, the answer is 4/3. A common factor of 5 was divided out of both the numerator and denominator.

What is the product of 5/14 and 7/20?

A product is found by multiplication. Multiplying two fractions together is easier when common factors are cancelled first to avoid working with larger numbers.

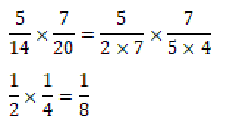
What is the result of dividing 24 by 8/5 ?

Division is completed by multiplying by the reciprocal. Therefore:

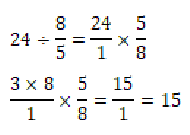
Subtract 5/14 from 5/24. What is the correct result?

Common denominators must be used. The LCD is 168, so each fraction must be converted to have 168 as the denominator.

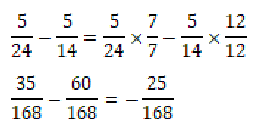
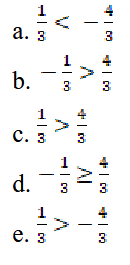
Which of the following is a correct mathematical statement?

The correct mathematical statement is the one in which the number to the left on the number line is less than the number to the right on the number line. It is written in answer E that 1/3 > -4/3, which is the same as -4/3 < 1/3, a correct statement.

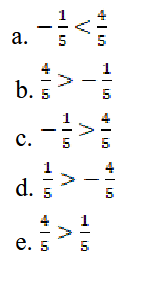
Which of the following is incorrect?

-1/5 > 4/5 is incorrect. The expression on the left is negative, which means that it is smaller than the expression on the right. As it is written, the inequality states that the expression on the left is greater than the expression on the right, which is not true.

In a neighborhood, 15 out of 80 of the households have children under the age of 18. What percentage of the households have children?

First, the information is translated into the ratio 15/80. To find the percentage, translate this fraction into a decimal by dividing 15 by 80. The corresponding decimal is 0.1875. Move the decimal point two units to the right to obtain the percentage 18.75%.

Gina took an algebra test last Friday. There were 35 questions, and she answered 60% of them correctly. How many correct answers did she have?

Gina answered 60% of 35 questions correctly; 60% can be expressed as the decimal 0.60. Therefore, she answered 0.60 × 35 = 21 questions correctly.

Paul took a written driving test, and he got 12 of the questions correct. If he answered 75% of the total questions correctly, how many problems were on the test?

The unknown quantity is the number of total questions on the test. Let x be equal to this unknown quantity. Therefore, 0.75x = 12. Divide both sides by 0.75 to obtain x = 16.

If a car is purchased for $15,395 with a 7.25% sales tax, what is the total price?

If sales tax is 7.25%, the price of the car must be multiplied times 1.0725 to account for the additional sales tax. Therefore, 15,395 × 1.0725 = 16,511.1375. This amount is rounded to the nearest cent, which is $16,511.14.

A car manufacturer usually makes 15,412 SUVs, 25,815 station wagons, 50,412 sedans, 8,123 trucks, and 18,312 hybrids a month. About how many cars are manufactured each month?

Rounding can be used to find the best approximation. All of the values can be rounded to the nearest thousand. 15,412 SUVs can be rounded to 15,000. 25,815 station wagons can be rounded to 26,000. 50,412 sedans can be rounded to 50,000. 8,123 trucks can be rounded to 8,000. Finally, 18,312 hybrids can be rounded to 18,000. The sum of the rounded values is 117,000, which is closest to 120,000.

Each year, a family goes to the grocery store every week and spends $105. About how much does the family spend annually on groceries?

There are 52 weeks in a year, and if the family spends $105 each week, that amount is close to $100. A good approximation is $100 a week for 50 weeks, which is found through the product 50 × 100 = $5,000.

Bindee is having a barbeque on Sunday and needs 12 packets of ketchup for every 5 guests. If 60 guests are coming, how many packets of ketchup should she buy?

This problem involves ratios and percentages. If 12 packets are needed for every 5 people, this statement is equivalent to the ratio 12/5. The unknown amount x is the number of ketchup packets needed for 60 people. The proportion 12/5 = x/60 must be solved. Cross-multiply to obtain 12 × 60 = 5x. Therefore, 720 = 5x. Divide each side by 5 to obtain x = 144 packets.

A grocery store sold 48 bags of apples in one day, and 9 of the bags contained Granny Smith apples. The rest contained Red Delicious apples. What is the ratio of bags of Granny Smith to bags of Red Delicious that were sold?

There were 48 total bags of apples sold. If 9 bags were Granny Smith and the rest were Red Delicious, then 48 – 9 = 39 bags were Red Delicious. Therefore, the ratio of Granny Smith to Red Delicious is 9:39.

If Oscar’s bank account totaled $4,000 in March and $4,900 in June, what was the rate of change in his bank account total over those three months?

The average rate of change is found by calculating the difference in dollars over the elapsed time. Therefore, the rate of change is equal to $4,900 - $4,000 / 3 months, which is equal to $900 / 3 or $300 a month.

How is a transposition of a matrix performed?

a. Multiply each number by negative 1

b. Switch the rows and columns

c. Reverse the order of each row

d. Find the inverse of each number

e. Divide the first number in each row by the last number in the last

column

The correct choice is B because the definition of transposing a matrix says that the rows and columns should be switched. For example, the vertical matrix in the photo can be transformed to

[ 3 2 1 ]

[ 4 5 6 ]

Notice that the first row, 3 and 4, becomes the first column. The second row, 2 and 5, becomes the second column. This is an example of transposing a matrix.

What is the label given to a problem that multiplies a matrix by a

constant?

a. Vector multiplication

b. Scalar multiplication

c. Inverse of a matrix

d. Transposition of a matrix

e. Product of a matrix

The correct answer is Choice B because multiplying a matrix by a constant is called scalar multiplication. A scalar is a constant number, which means the only thing it changes about a matrix is its magnitude. For a given matrix,

[ 3 6 ]

[ 4 5 ],

scalar multiplication can be applied by multiplying by 2, which yields the matrix

[ 6 8 ]

[ 12 10 ].

Notice that the dimensions of the matrix did not change, just the magnitude of the numbers.

What are the two values that always describe a vector?

a. Magnitude and direction

b. Magnitude and length

c. Length and position

d. Direction and position

e. Magnitude and position

The vector is described as having both magnitude and direction. The magnitude is the size of the vector and the direction is the path along with which the force is being applied. The second answer choice has magnitude and length, which are essentially the same. The third, fourth, and fifth answer choices include length and position, but position is also not part of the description of a vector.

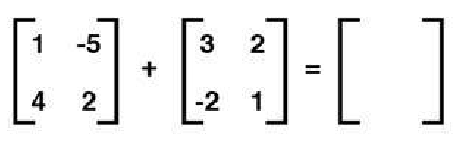
What is the resultant matrix when addition is performed?

The correct answer is

[ 4 -3 ]

[ 2 3 ]

Matrices are added by adding the corresponding numbers in the two given matrices. For matrices to be added, they must have the same number of rows and columns. These two matrices have two rows and two columns. The first row, first column numbers are 1 and 3, and adding them together yields a total of 4. The second row, first column has numbers 4 and –2, which yields a sum of 2. The first row, second column has –5 and 2, which sum to –3. The second row, second column have 2 and 1, which yield a sum of 3.

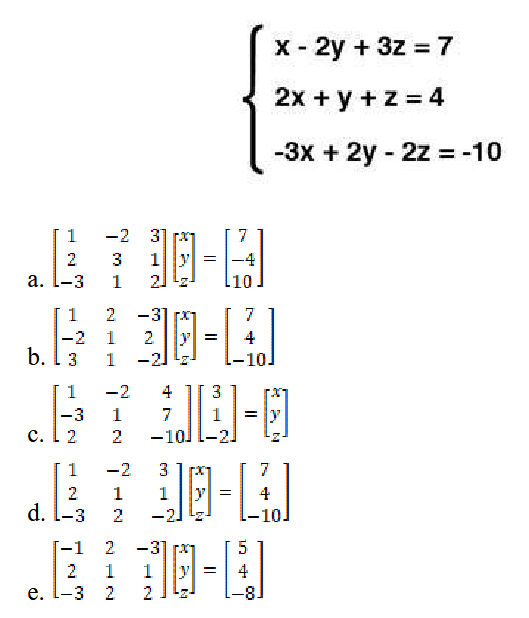
Which set of matrices represents the following system of equations?

The correct matrix to describe the given system of equations is the last matrix (Choice D) because it has values that correspond to the coefficients in the right order. The top row corresponds to the coefficient in the first equation, the second row corresponds to the coefficients in the second equation, and the third row corresponds to the coefficients in the third equation. The second matrix (Choice B) is filled with the three variables in the system. One thing to also look for is the sign on the numbers, to make sure the signs are correct from the equation to the matrix.

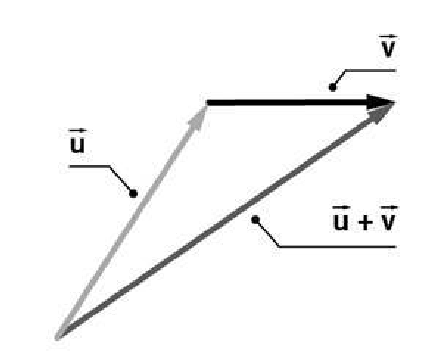
Which label describes the relationship between these vectors?

a. Vector magnitude

b. Vector extraction

c. Scalar vectors

d. Vector addition

e. Scalar magnitude

The picture shows how vectors are added. According to the definition, the vectors must be placed head to tail, then the resulting vector is drawn from the beginning head to the ending tail. Notice that the vector runs from the bottom left to the top right. Adding these vectors in the wrong direction would yield a vector starting at the top right, at the end of vector v, and ending at the bottom left.

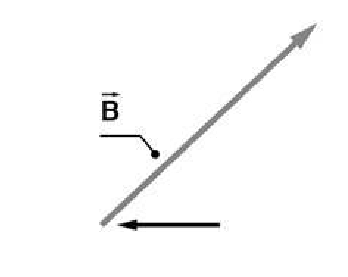
What is the name of the indicated part of Vector B?

a. Head

b. Tail

c. Magnitude

d. Direction

e. Point

The answer is Choice B because the part of the vector that the arrow points to is the tail. The end of a vector with the arrow is called the head. The opposite end, without the arrow, is called the tail.

When two vectors are added, what is the answer called?

a. Ending vector

b. Total vector

c. Summation vector

d. Resolved vector

e. Resultant vector

When two vectors are added, the resulting vector is called the resultant. By definition, the vector found from addition of two or more vectors is the resultant. The other choices of ending vector and total vector could refer to one or more of the starting vectors, not the resultant.