Functional Programming

program

description of a specific computation

function

a rule that associates to each x from some set X of values a unique y from a set Y of values.

domain

The set X is called the ____________ of f.

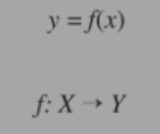
range

set Y is called the ________ of f.

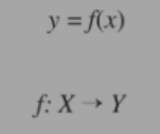
independent variable

The x in f(x), which represents any value from X

dependent variable

the y from the set Y, defined by the equation y = f(x)

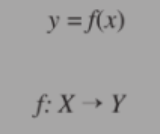
partial function

Sometimes f is not defined for all x in X

total

function that is defined for all x in X

function definition

describes how a value is to be computed using formal

parameters.

function application

a call to a defined function using actual parameters, or the values that the formal parameters assume for a particular computation

In imperative programming, variables refer to memory locations that store values. In functional programming, variables are bound to values and cannot change.

What is a key difference between imperative and functional programming regarding variables?

In mathematics, variables always stand for actual values and do not refer to memory locations or assignments, unlike imperative programming.

How does mathematics treat variables compared to programming?

Imperative Programming (Variables)

variables refer to memory locations that store values, allowing their contents to change over time.

Functional Programming (Variables)

variables are bound to values rather than memory locations. Once assigned, their values cannot change.

Variable in Mathematics

a variable always represents a fixed value and does not refer to a memory location or allow reassignment.

Composition

An operation on functions that takes two functions as parameters and produces a new function as the result.

Higher-Order Function

A function that takes other functions as parameters, returns a function, or both.

Delayed Evaluation

A strategy where function parameters are not evaluated immediately but only when their values are needed.

Applicative Order Evaluation

An evaluation rule where all parameters of a function are evaluated at the time of the function call, regardless of necessity.

Short-Circuit Evaluation

A Boolean evaluation technique where further computation stops as soon as the result is determined, such as in and and or expressions.

Nonstrict Function

A function that can produce a result even when some of its parameters are undefined or contain incomplete data.

Strict Function

A function that requires all parameters to be fully evaluated before execution, making implementation simpler but less flexible.

TRUE

Delayed evaluation allows nonstrict functions to return well-defined results even when some sub-expressions are undefined. TRUE OR FALSE

Lazy Evaluation

A strategy where expressions are only evaluated when their values are needed, allowing efficient computation and handling of infinite structures.

Stream

A partially computed list where elements are generated on demand, enabling the handling of potentially infinite lists in functional programming.

Lambda Calculus

was invented by Alonzo Church (1903 -1995), a mathematician in Princeton University.

Lambda Calculus

• It would be a function that takes a single input called x, process it in some way and produces the output, the number x+1 that refers to as increment of x.

• purely mathematical function and there’s no internal state that we can look inside a function.

• the variables

• the lambda notation build functions

• a way of applying functions.

Lambda Calculus only got three things, which are:

Lisp

A functional programming language developed in the 1950s–1960s, designed for list processing and based on lambda calculus.

John McCarthy

Developed Lisp

Scheme

A dialect of Lisp that follows the principles of functional programming and is influenced by lambda calculus.

Uniform Representation

Scheme represents both programs and data using a single general data structure—the list.

Metacircular Interpreter

An interpreter written in the same language it interprets, used to define the language itself in Scheme.

Automatic Memory Management

Scheme's run-time system automatically handles memory allocation and garbage collection.

Atoms

are like the literal constants and identifiers of an imperative language, the include numbers, characters, strings, names, functions, and a few other constructs.

parenthesized expression

sequence of zero or more expressions separated by spaces

and surrounded by parentheses

extended Backus-Naur form

This syntax is expressed in a notation called?

Atomic Literals in Scheme

Numbers, characters, and strings that evaluate to themselves without requiring further computation.

Identifiers in Scheme

Symbols (except keywords) that are looked up in the current environment and replaced by their associated values.

Environment in Scheme

A symbol table that stores variable bindings and their corresponding values.

Applicative Order Evaluation in Scheme

A strategy where all sub-expressions are evaluated first, following a bottom-up traversal of the expression tree.

ML (MetaLanguage)

A functional programming language developed in the late 1970s as part of the Edinburgh Logic for Computable Functions (LCF) system.

Edinburgh Logic for Computable Functions (LCF)

A system designed for proving program correctness, which led to the development of ML.

Robin Milner

A key developer of ML and the Hindley-Milner type inference system.

Hindley-Milner Type Checking

A strong type inference system based on pattern matching, used in ML and Haskell.

Haskell

a pure functional language whose development began in the late 1980s, primarily at Yale University and the University of Glasgow. Known for lazy evaluation and advanced functional features.

David A. Turner

A key figure in the development of purely functional lazy languages, leading to the Miranda programming language, which influenced Haskell.

Monads

A mechanism used to handle side effects, such as I/O, in a pure functional programming paradigm.

Layout Rule in Haskell

A rule that uses indentation and formatting instead of explicit syntax elements like semicolons or brackets.