Chapter 9: Conceptual Knowledge Pt 1 (Definitional + Prototype)

By Jordana Burstein for Cognition

Why are categories and concepts necessary in life? (concepts and categories)

Categories and concepts help us organize and simplify our experiences, making it easier to recognize patterns, remember information, communicate efficiently, and make sense of the world. Without them, language and thought would be chaotic and overwhelming.

What are the three main functions of categories and concepts? (concepts and categories)

1. Classification – Allows us to treat different things as the same based on shared features.

2. Communication – Enables us to use words to refer to concepts, simplifying language.

3. Prediction – Helps us infer unobserved properties based on past knowledge.

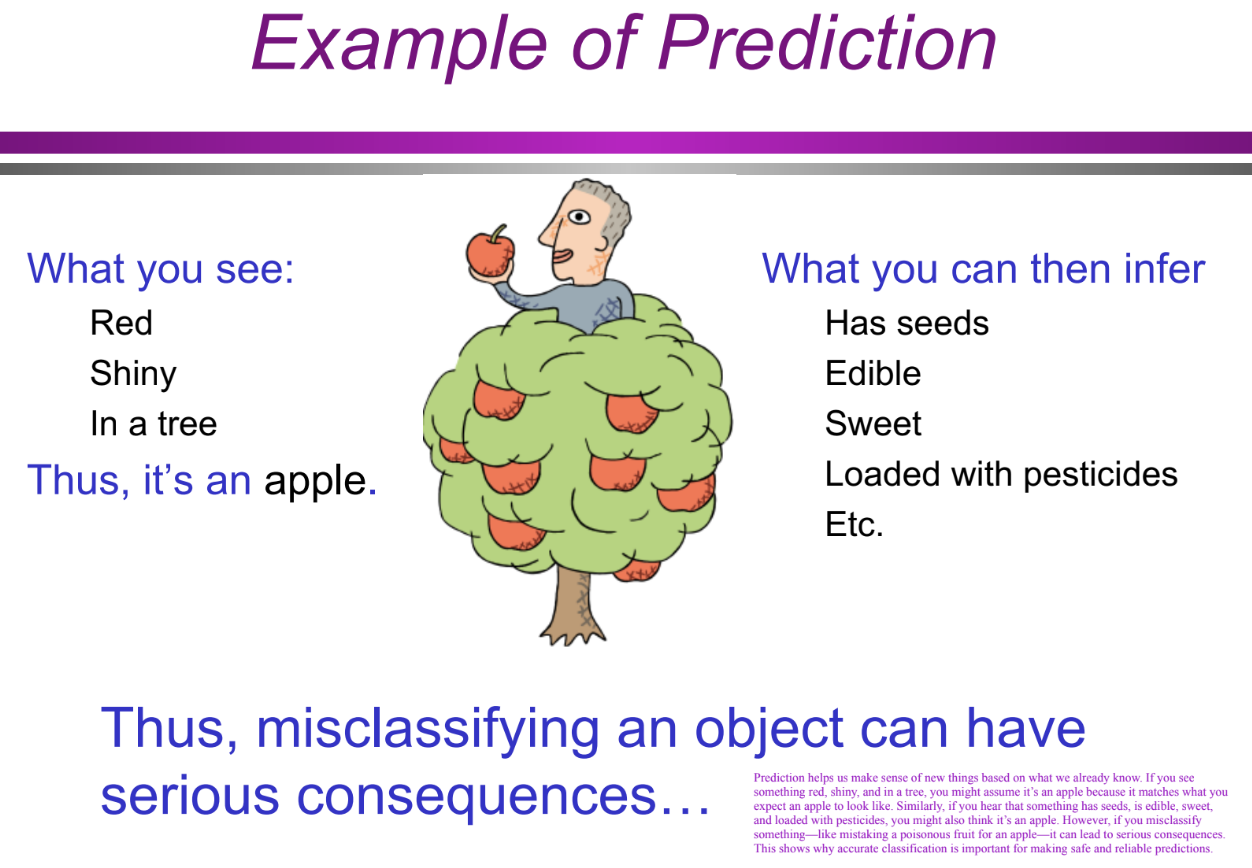
How does prediction work in categorization, and why is it important? (concepts and categories)

If you see something red, shiny, and in a tree, you might predict it’s an apple based on past experiences. However, misclassifying objects can have serious consequences—mistaking a poisonous fruit for an apple could be dangerous. This highlights the importance of accurate classification for making safe and reliable predictions.

What key questions do categorization theories try to answer? (Categorization/Conceptual Structure)

Categorization theories seek to explain:

1. How are categories represented?

2. How are new objects classified?

3. How are categories used to make inferences?

What do categorization theories assume about categories? (Categorization/Conceptual Structure)

They assume that categories consist of features (e.g., parts, attributes, properties) that help us recognize and group similar things together.

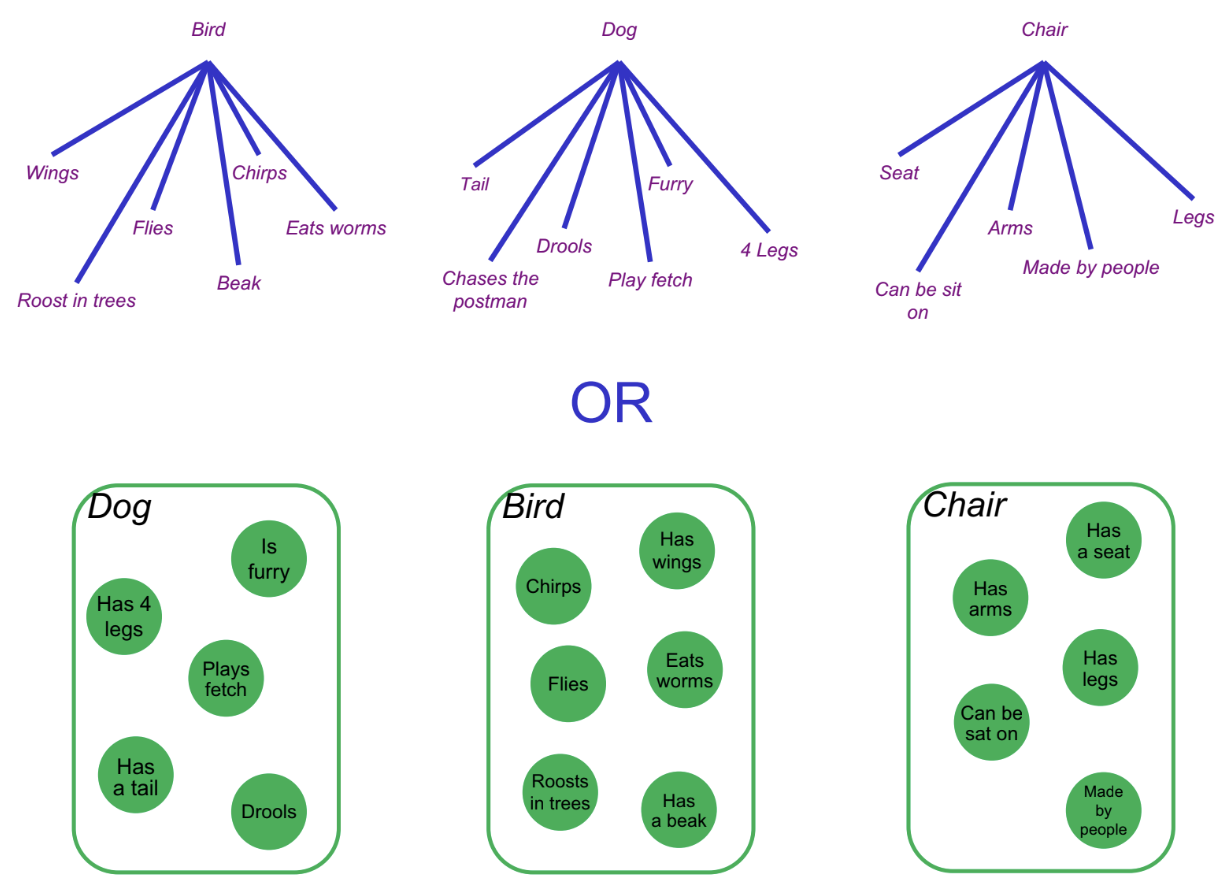
How do features help categorize objects like dogs, birds, and chairs? (Categorization/Conceptual Structure)

Objects are categorized based on shared features:

• A dog has fur, four legs, a tail, drools, and plays fetch.

• A bird has wings, a beak, chirps, flies, eats worms, and roosts in trees.

• A chair has a seat, legs, arms, is made by people, and is designed for sitting.
  By recognizing these features, we can quickly classify new objects and make predictions about them.

What are the three main theories of classification and conceptual structure? (Categorization/Conceptual Structure)

• Definitional-based approaches – Categories are defined by a set of necessary and sufficient features.

• Probabilistic/similarity-based views – Categorization is based on resemblance rather than strict definitions.

  • Prototype models – New objects are compared to an ideal or average category member.

  • Exemplar models – New objects are compared to specific past examples.

• Causal model views – Categories are understood through cause-and-effect relationships between features.

  • Essentialism – Assumes that categories have an underlying essence that makes them what they are, even if outward appearances differ.

What is the definitional approach to categorization? (Categorization/Conceptual Structure: definitional approach)

The definitional approach, rooted in Aristotle’s philosophy, suggests that concepts function like definitions. Categories have defining features that determine membership, meaning an object must meet specific criteria to belong to a category.

What are defining features? (Categorization/Conceptual Structure: definitional approach)

Defining features are the essential characteristics an object must have to be considered part of a category. These features determine whether something belongs to a category under the definitional approach.

What are the two inferences that definitions support in the definitional approach? (Categorization/Conceptual Structure: definitional approach)

1. Necessity – If something belongs to a category, it must have the defining features.

2. Joint sufficiency – If something has all the defining features, it must belong to the category.

What is necessity in the definitional approach? (Categorization/Conceptual Structure: definitional approach)

Necessity means that if an object is a member of a category, it must have all of the category’s defining features.

What is joint sufficiency in the definitional approach? (Categorization/Conceptual Structure: definitional approach)

Joint sufficiency means that if an object has all the defining features of a category, it must belong to that category.

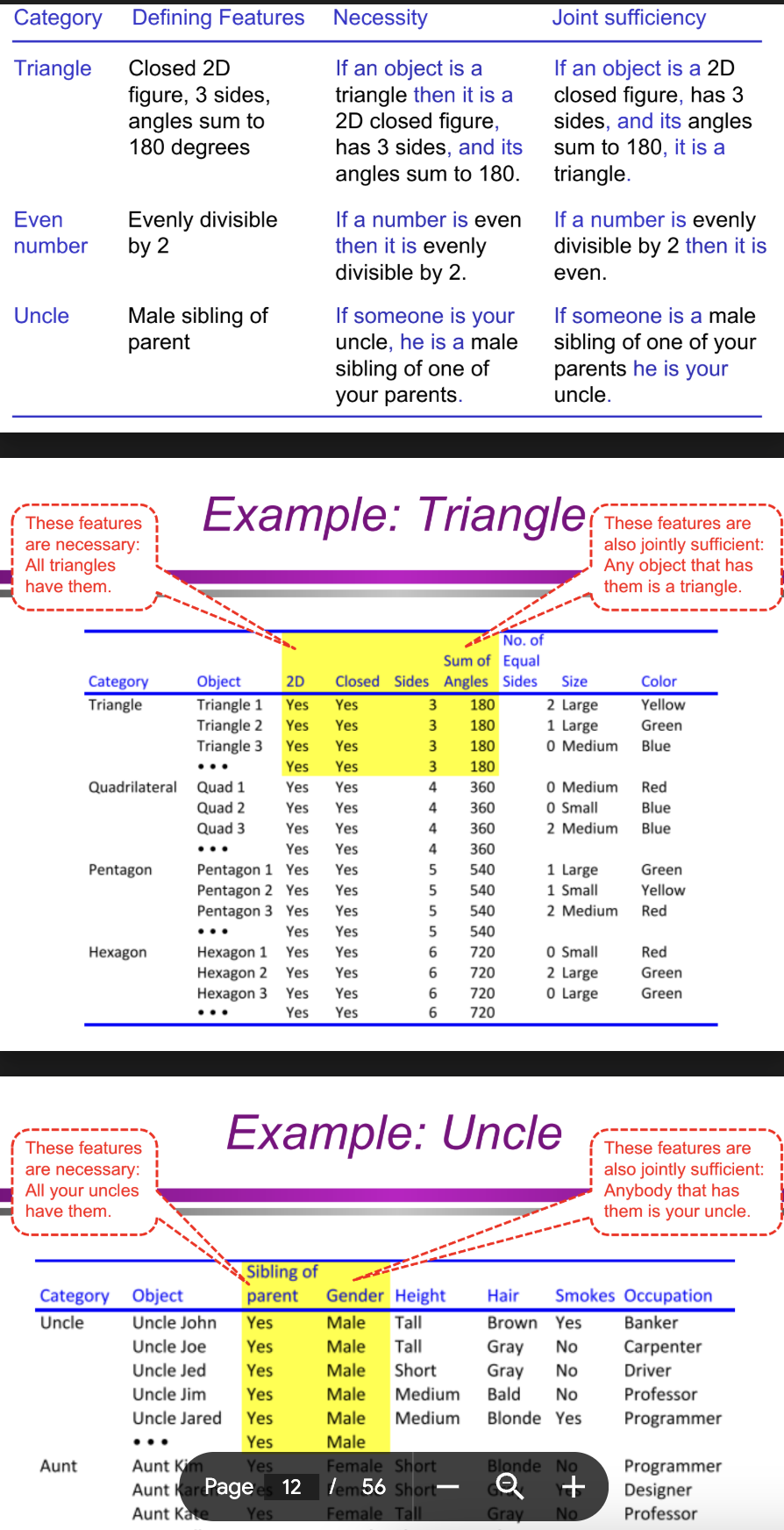
How does the definitional approach apply to the concept of a triangle? (Categorization/Conceptual Structure: definitional approach)

A triangle is defined as a 2D closed figure with three sides and angles summing to 180 degrees.

• Necessity: All triangles must have these features.

• Joint sufficiency: Any shape with these features is a triangle.

How does the definitional approach apply to the concept of an uncle? (Categorization/Conceptual Structure: definitional approach)

An uncle is defined as a male sibling of one of your parents.

• Necessity: All uncles must be male and a sibling of a parent.

• Joint sufficiency: Any person who meets these conditions is an uncle.

How are definition-based categories learned? (Categorization/Conceptual Structure: definitional approach)

Learning definition-based categories involves hypothesis testing or rule discovery. People test different features to determine which ones are necessary and jointly sufficient for category membership. This process helps identify strict definitions for concepts.

What are the three tests of the definitional approach? (Categorization/Conceptual Structure: definitional approach)

1. Existence of defining features – Do categories have features that are both necessary and jointly sufficient?

2. Ambiguous category membership – Are some objects difficult to classify?

3. Graded category membership – Are some category members seen as more typical than others?

What is the first test of the definitional approach? (Categorization/Conceptual Structure: definitional approach)

The existence of defining features test examines whether people can identify features that are both necessary and jointly sufficient for category membership. Many features that come to mind may be necessary but are not jointly sufficient, making it difficult to define categories strictly.

Why do the commonly listed features of a dog fail as defining features? (Categorization/Conceptual Structure: definitional approach)

• Commonly listed features (e.g., four legs, plays fetch, chases mailmen, has fur) are not necessary because some dogs lack them (e.g., three-legged dogs, dogs that don’t fetch).

• More fundamental features (e.g., has lungs, needs food, breathes air) are necessary but not jointly sufficient because other animals (cats, raccoons) also have them.

• This shows that finding a strict set of defining features for "dog" is difficult.

Why do the commonly listed features of a chair fail as defining features? (Categorization/Conceptual Structure: definitional approach)

• Commonly listed features (e.g., four legs, has a back, can be sat on) are not necessary because some chairs lack them (e.g., bean bag chairs, bar stools).

• More general features (e.g., man-made, used by humans, costs money) are necessary but not jointly sufficient because other objects (bookshelves, refrigerators) share these features.

• This shows that defining categories like "chair" with strict features is challenging.

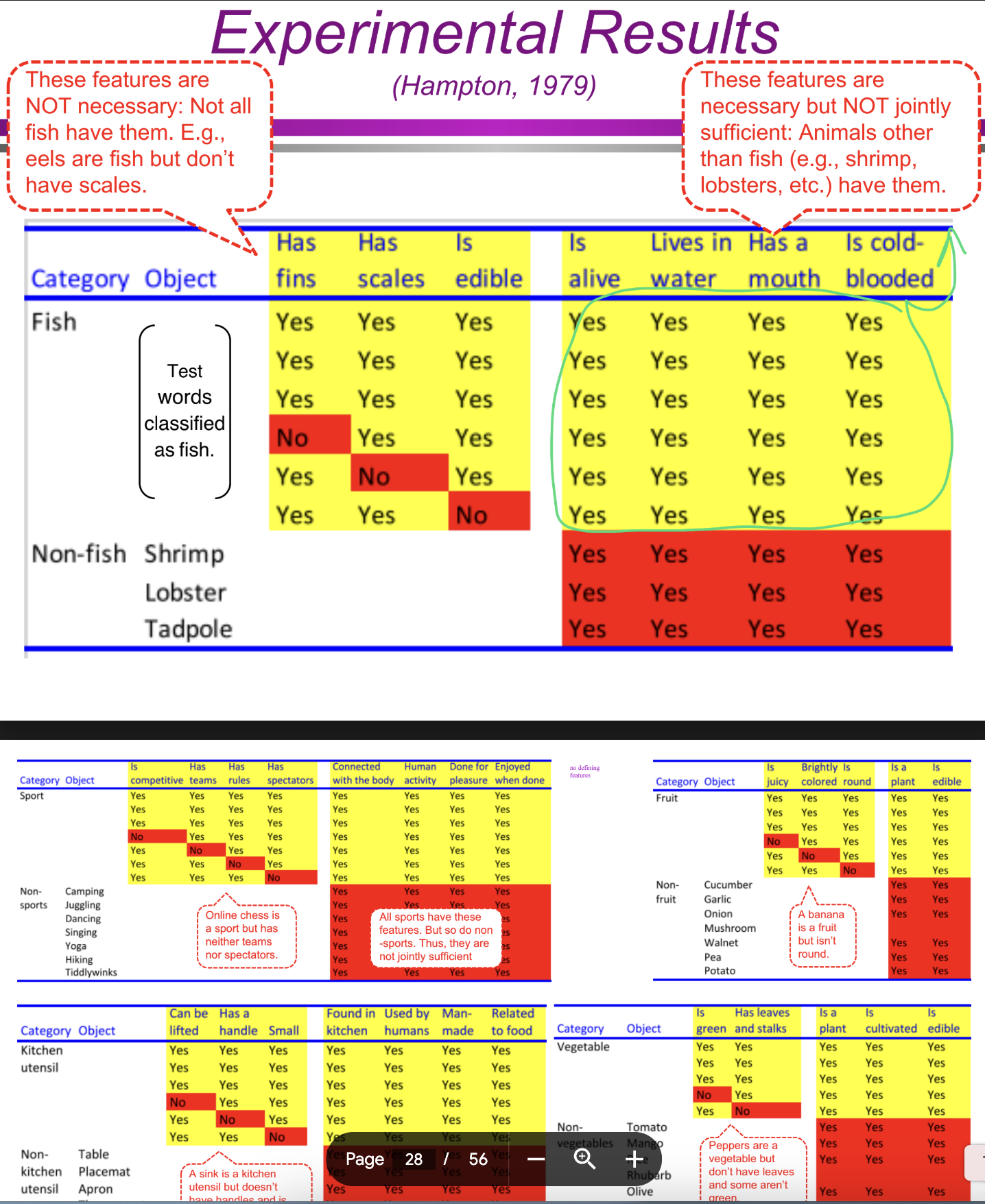
What was the general aim of James Hampton’s (1979) study? (Categorization/Conceptual Structure: definitional approach)

Hampton aimed to test whether common categories have defining features that are both necessary and jointly sufficient for membership. He investigated whether people could identify strict category-defining features in everyday concepts like "fruit" and "fish."

What were the specific steps of Hampton’s (1979) procedure? (Categorization/Conceptual Structure: definitional approach)

1. Participants listed features for eight common superordinate categories (e.g., fruit, fish, sport, vegetable, bird, furniture, vehicle, kitchen utensil).

2. Only features mentioned by a substantial number of participants were retained.

3. Participants judged whether 30 test words (e.g., trout, shrimp, shark, lobster for "fish") belonged to each category.

4. A separate group listed features for the test words.

5. The categories were analyzed to determine whether the listed features were necessary and jointly sufficient for categorization.

What were the results of Hampton’s (1979) study? (Categorization/Conceptual Structure: definitional approach)

• Some category members lacked commonly assumed defining features (e.g., eels are fish but don’t have scales).

• Some features were necessary but not jointly sufficient (e.g., having scales is common for fish, but shrimp and lobsters also have them and are not fish).

• This demonstrated that strict defining features are difficult to identify for everyday categories.

What is the evidence against defining features? (Categorization/Conceptual Structure: definitional approach)

• People are often unable to identify defining features for many everyday categories.

• This suggests that many categories do not have strict necessary and sufficient features.

• However, the inability to consciously identify defining features does not mean the brain doesn’t use them for classification.

• Two stronger tests are needed to further investigate how categorization works.

What is the second test of the definitional approach? (Categorization/Conceptual Structure: definitional approach)

The second test is Unambiguous Category Membership. The definitional approach predicts that category membership should be clear-cut—something either belongs to a category or it does not. There should be no borderline cases. For example, a shape is either a triangle or not, a number is either even or not, and a person is either your uncle or not. However, research suggests that real-world categories often have ambiguous cases.

What is a borderline case in categorization? (Categorization/Conceptual Structure: definitional approach)

A borderline case is an item that does not clearly belong to one category or another. For example, people may be uncertain whether a pumpkin is a fruit, whether a rug is furniture, or whether a leech is an insect. The definitional approach predicts that no borderline cases should exist, but studies show that they are common.

What are some examples of borderline cases in categorization? (Categorization/Conceptual Structure: definitional approach)

• Furniture: A shelf (76% say yes), a rug (52%), a lampshade (63%), bookends (57%), a candlestick (28%).

• Fruit: An acorn (60%), an olive (60%), a pumpkin (53%).

• Other examples: Is sugar cane a vegetable? Is yeast an animal? Is a rowboat a ship?

These results show that many objects do not have clear-cut category membership, contradicting the definitional approach.

What was the aim of McCloskey & Glucksberg’s 1978 study? (Categorization/Conceptual Structure: definitional approach)

The study aimed to test whether category membership is unambiguous, as predicted by the definitional approach. If categories have strict defining features, then people should consistently classify items without disagreement or hesitation. However, the study investigated whether people classify items inconsistently, especially for borderline cases.

What was the procedure of McCloskey & Glucksberg’s (1978) study? (Categorization/Conceptual Structure: definitional approach)

1. Participants were asked to judge whether various objects belonged to everyday categories (e.g., “Is a pumpkin a fruit?” “Is a rug furniture?”).

2. One month later, participants were asked the same categorization questions again.

3. Researchers analyzed how often participants’ answers changed over time to measure uncertainty.

What were the specific results of McCloskey & Glucksberg’s (1978) study? (Categorization/Conceptual Structure: definitional approach)

• Many objects were identified as borderline cases, meaning some participants classified them as category members while others did not.

• Example: Only 60% of participants agreed that an acorn is a fruit, and only 53% agreed that a pumpkin is a fruit.

• This contradicts the idea that categories have strict, defining features.

What does “uncertainty within subjects” mean, and how was it tested? (Categorization/Conceptual Structure: definitional approach)

Uncertainty within subjects refers to the idea that individuals may change their own minds about category membership over time, rather than uncertainty only existing between different people. McCloskey & Glucksberg tested this by re-examining participants one month later to see if they answered the same questions differently.

What were the results after one month, and what do they show about uncertainty? (Categorization/Conceptual Structure: definitional approach)

After one month, participants changed their minds about borderline cases 22% of the time, proving that categorization uncertainty exists within individuals, not just between different people.

• Example:

  • “Is a stroke a disease?” – 37% changed their answer.

  • “Is a pumpkin a fruit?” – 27% changed their answer.

  • “Is a leech an insect?” – 10% changed their answer.
    These results challenge the definitional approach because they show that even the same person does not always categorize objects consistently.

What is the third test of the definitional approach? (Categorization/Conceptual Structure: definitional approach)

The third test is Ungraded Category Membership, which suggests that all category members should be equal. If the definitional approach were correct, no category member would be considered a "better" or "worse" example than another. However, research suggests that some members are seen as more representative than others.

What does "ungraded" mean in the context of category membership? (Categorization/Conceptual Structure: definitional approach)

"Ungraded" means that all category members are equally valid and representative of the category. For example, under this view, all triangles are equally good triangles, all even numbers are equally even, and all uncles are equally uncles. However, real-world categorization often shows that some examples are seen as "better" or more typical than others.

What are some examples that illustrate the idea of ungraded category membership? (Categorization/Conceptual Structure: definitional approach)

• Shapes: A triangle is as much a triangle as any other.

• Numbers: An even number is just as even as any other even number.

• Family Relations: An uncle is just as much an uncle as any other.

However, studies show that real-world categories often have members that are perceived as better or worse examples of the category.

What was the aim of Eleanor Rosch’s 1973 study? (Categorization/Conceptual Structure: definitional approach)

The aim was to test whether category membership is ungraded by investigating whether people perceive some members as better examples of a category than others. If the definitional approach were correct, all members should be judged as equally representative, but Rosch hypothesized that some would be seen as more typical than others.

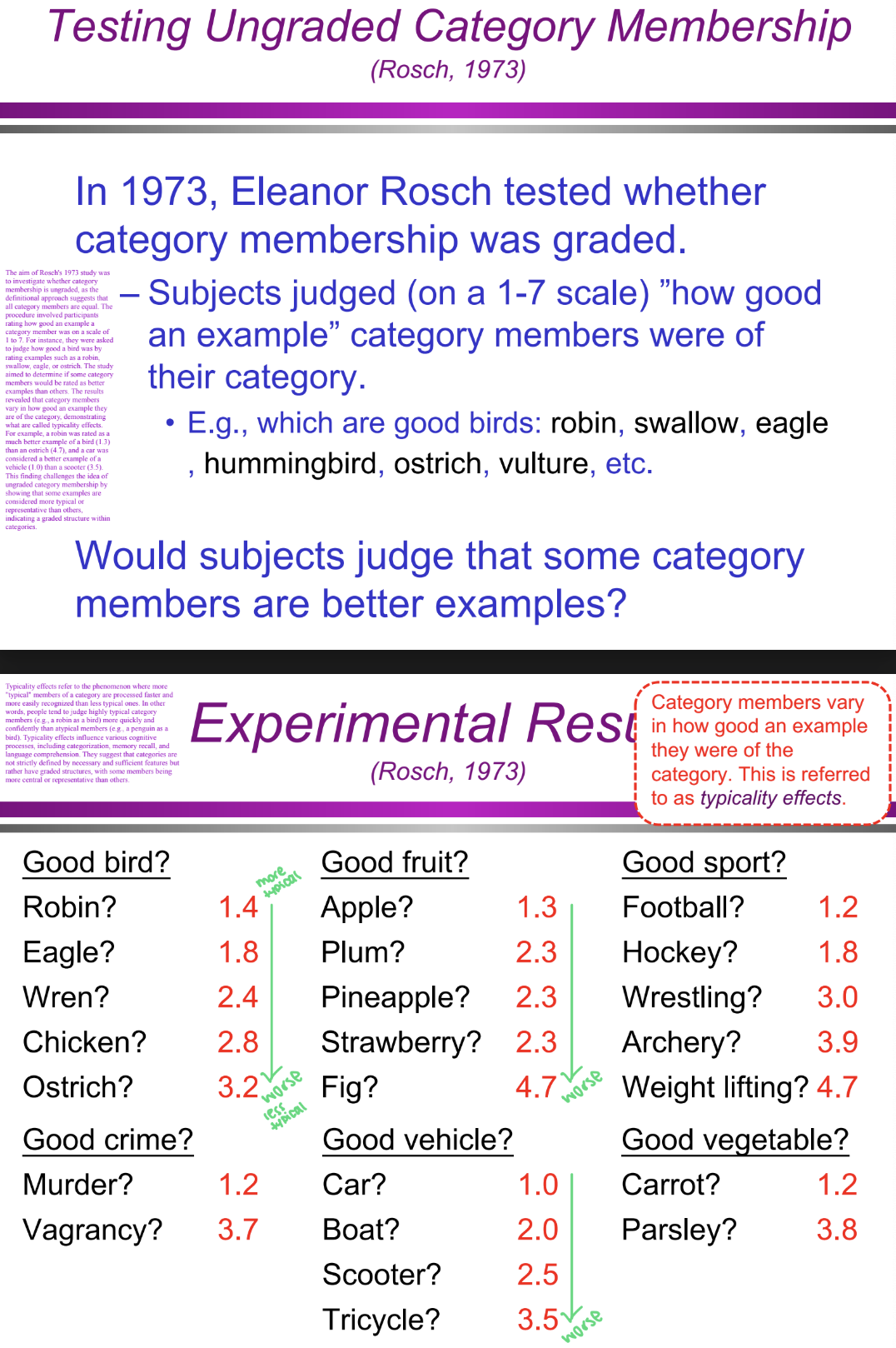
What were the steps of Eleanor Rosch’s (1973) study? (Categorization/Conceptual Structure: definitional approach)

1. Participants were given a list of category members (e.g., different birds, fruits, vehicles).

2. They rated each member on a 1-7 scale, indicating how "good" an example it was of the category.

3. Researchers analyzed the ratings to see if some category members were judged as more typical than others.

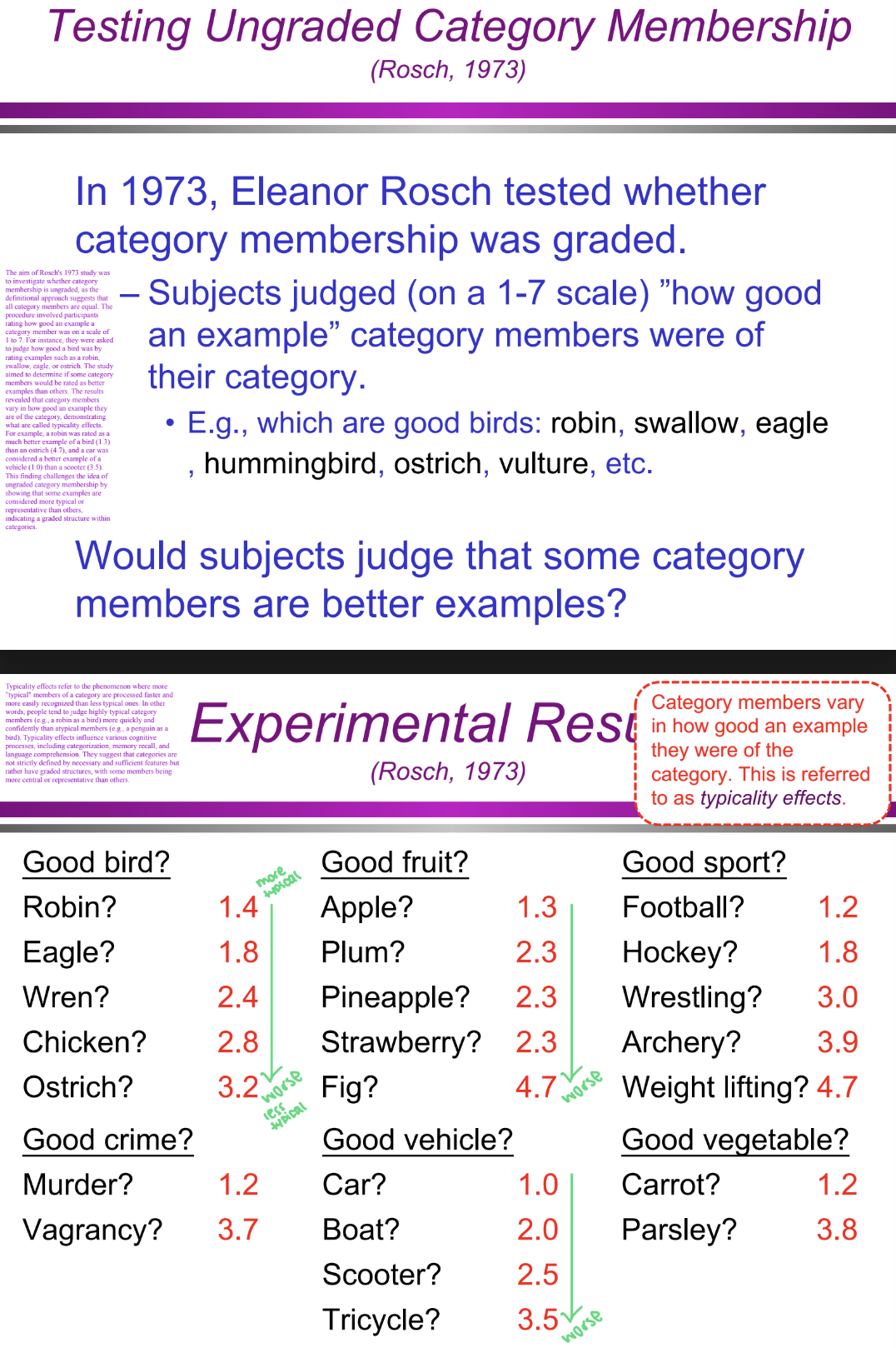
What were the specific results of Rosch’s (1973) study? (Categorization/Conceptual Structure: definitional approach)

• Birds: A robin was rated as a better bird (1.4) than an ostrich (3.2).

• Fruits: An apple was rated as a better fruit (1.3) than a fig (4.7).

• Sports: Football was rated as a better sport (1.2) than weightlifting (4.7).

• Vehicles: A car was rated as a better vehicle (1.0) than a tricycle (3.5).

These results show that category membership is graded, meaning some members are seen as more central or typical than others.

Category members vary in how good an example they were of the category, which is referred to as typicality effects.

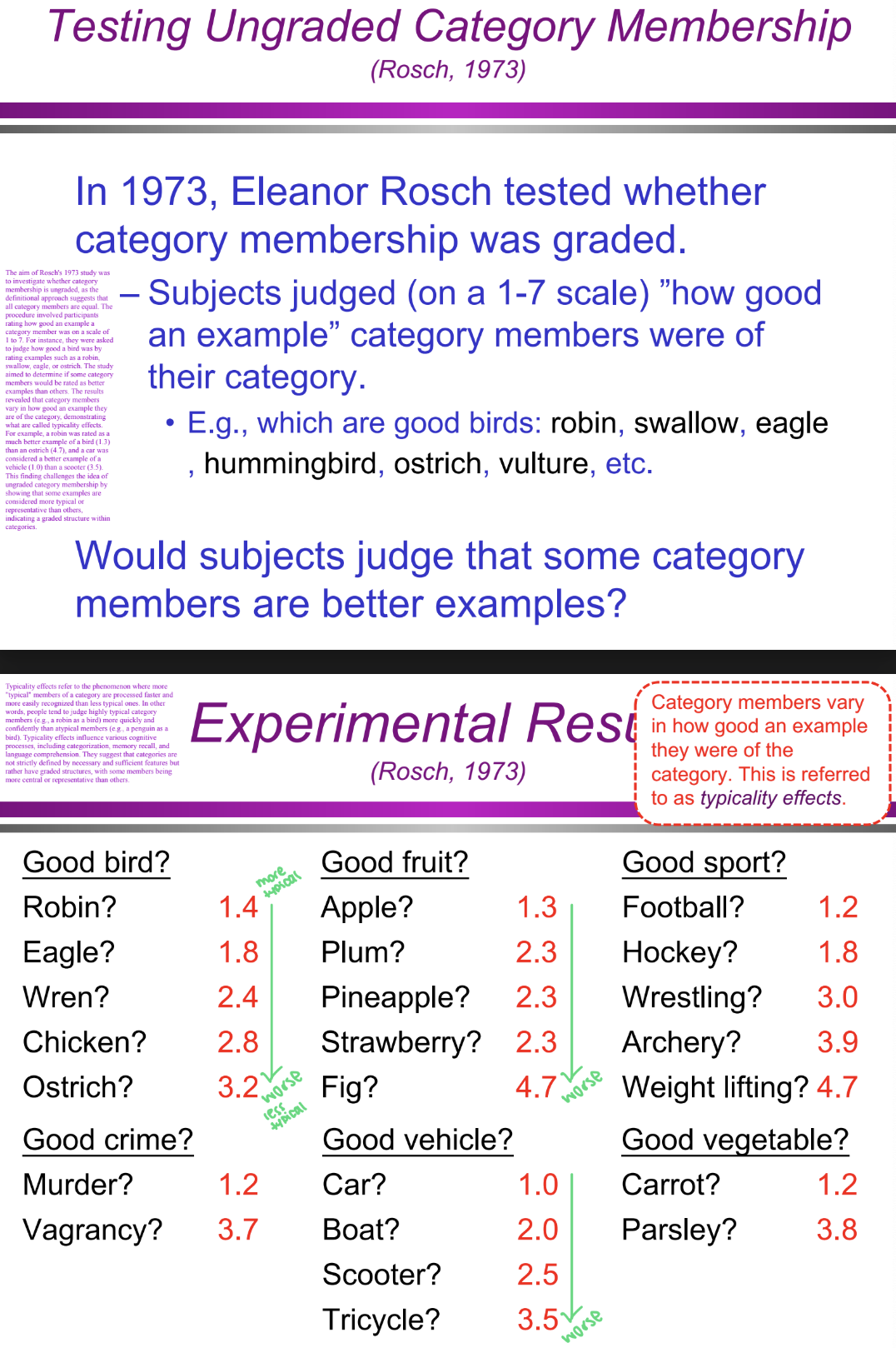
What are typicality effects? (Categorization/Conceptual Structure: definitional approach)

Typicality effects refer to the phenomenon where more "typical" category members are processed faster, recognized more easily, and judged more confidently than less typical ones. For example, people identify a robin as a bird more quickly than a penguin. This challenges the definitional approach, suggesting that categories have graded structures, where some members are more representative than others.

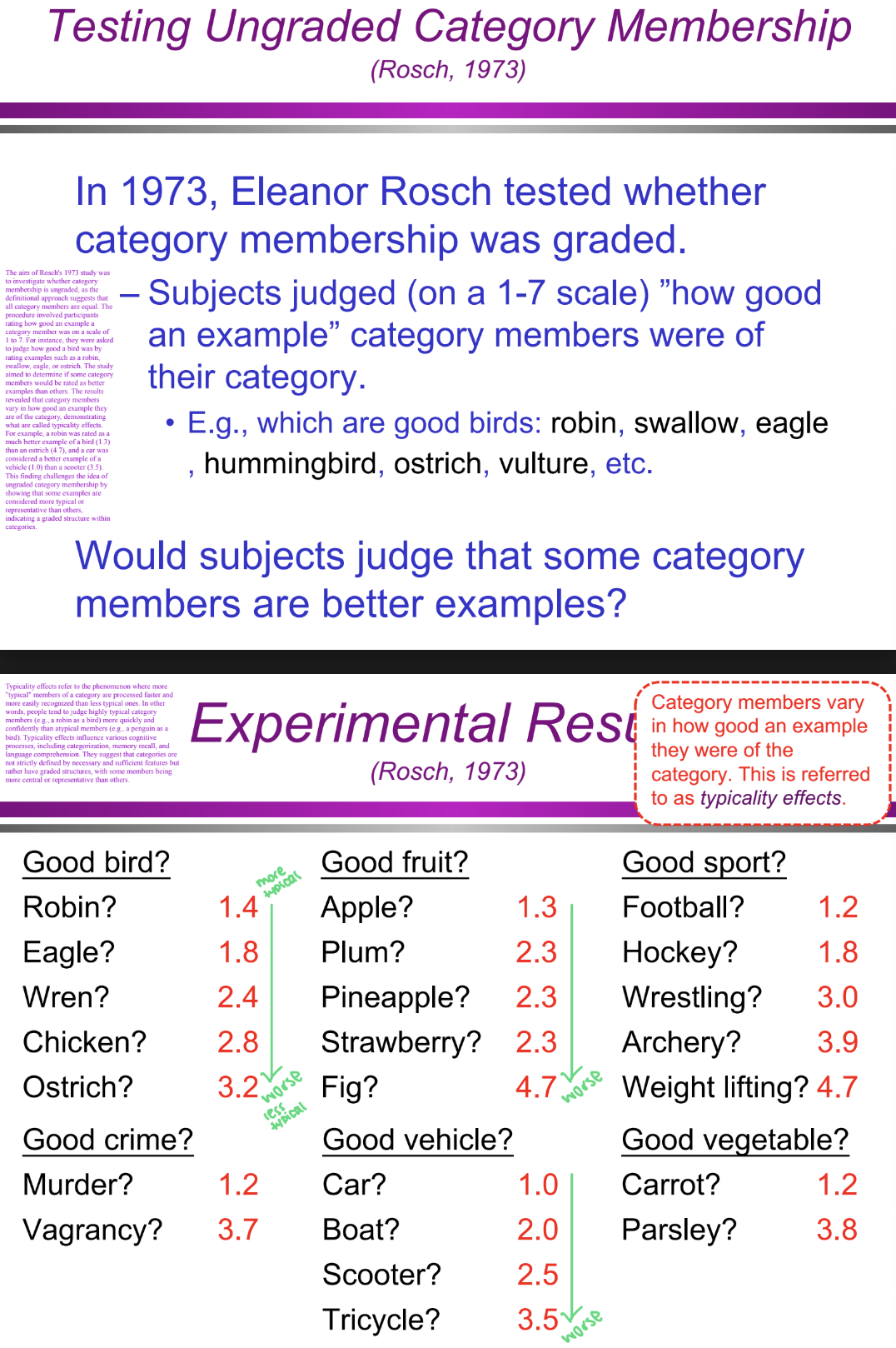
Why do typicality effects occur? (Categorization/Conceptual Structure: definitional approach)

Typicality effects occur because category members with high family resemblance are perceived as more typical. That is, typical category members share many features with other members of the category, making them easier to recognize, process, and categorize quickly.

What was the aim of Rosch & Mervis’s (1975) study? (Categorization/Conceptual Structure: definitional approach)

The study aimed to explore why some category members are considered more typical than others. Rosch and Mervis hypothesized that family resemblance—the degree to which an item shares features with other category members—determines typicality.

What is family resemblance in categorization? (Categorization/Conceptual Structure: definitional approach)

Family resemblance refers to the idea that category members do not share a single defining feature but are linked by overlapping similarities. This means that some members appear more typical because they share many features with other members, while others appear less typical due to fewer shared features.

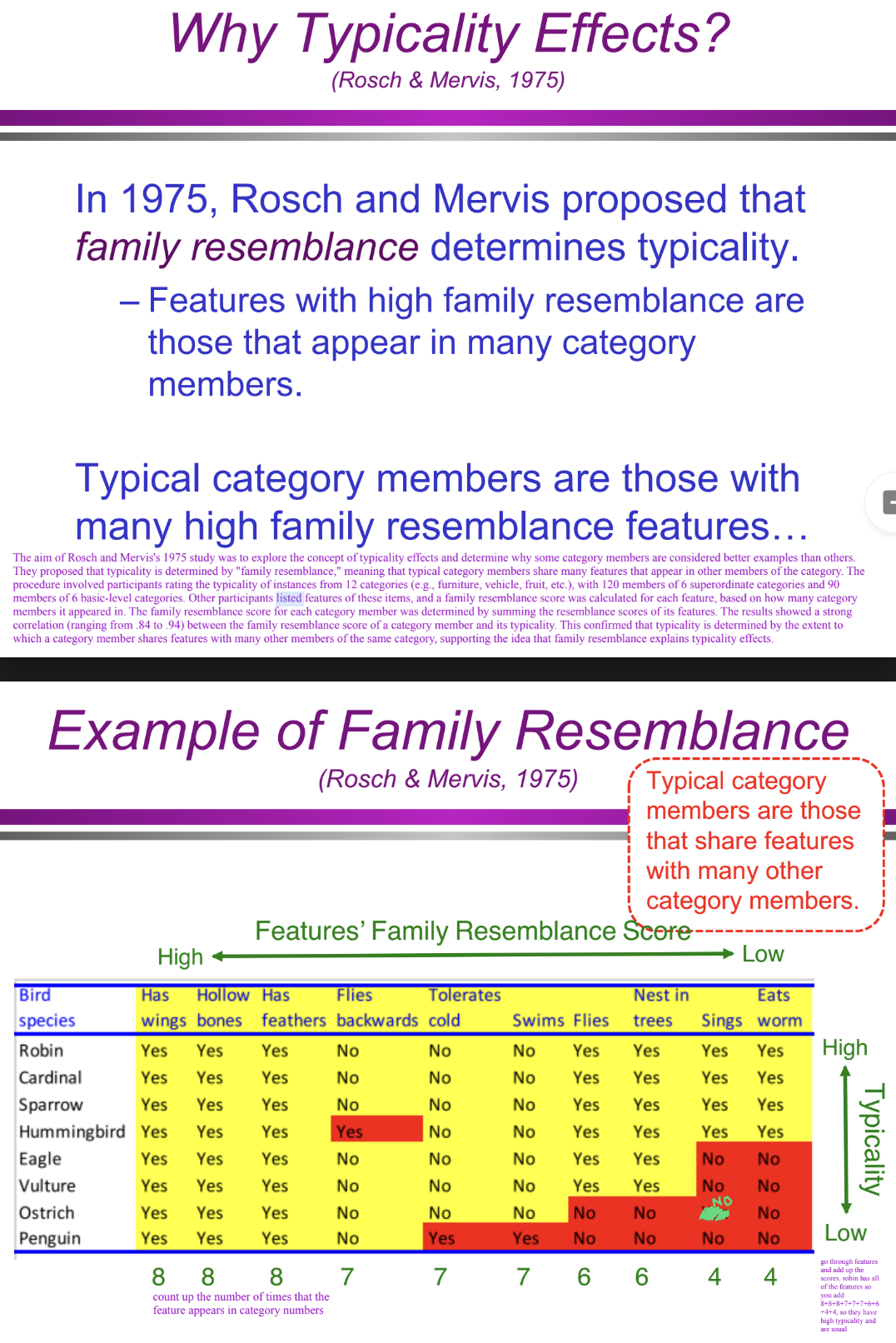
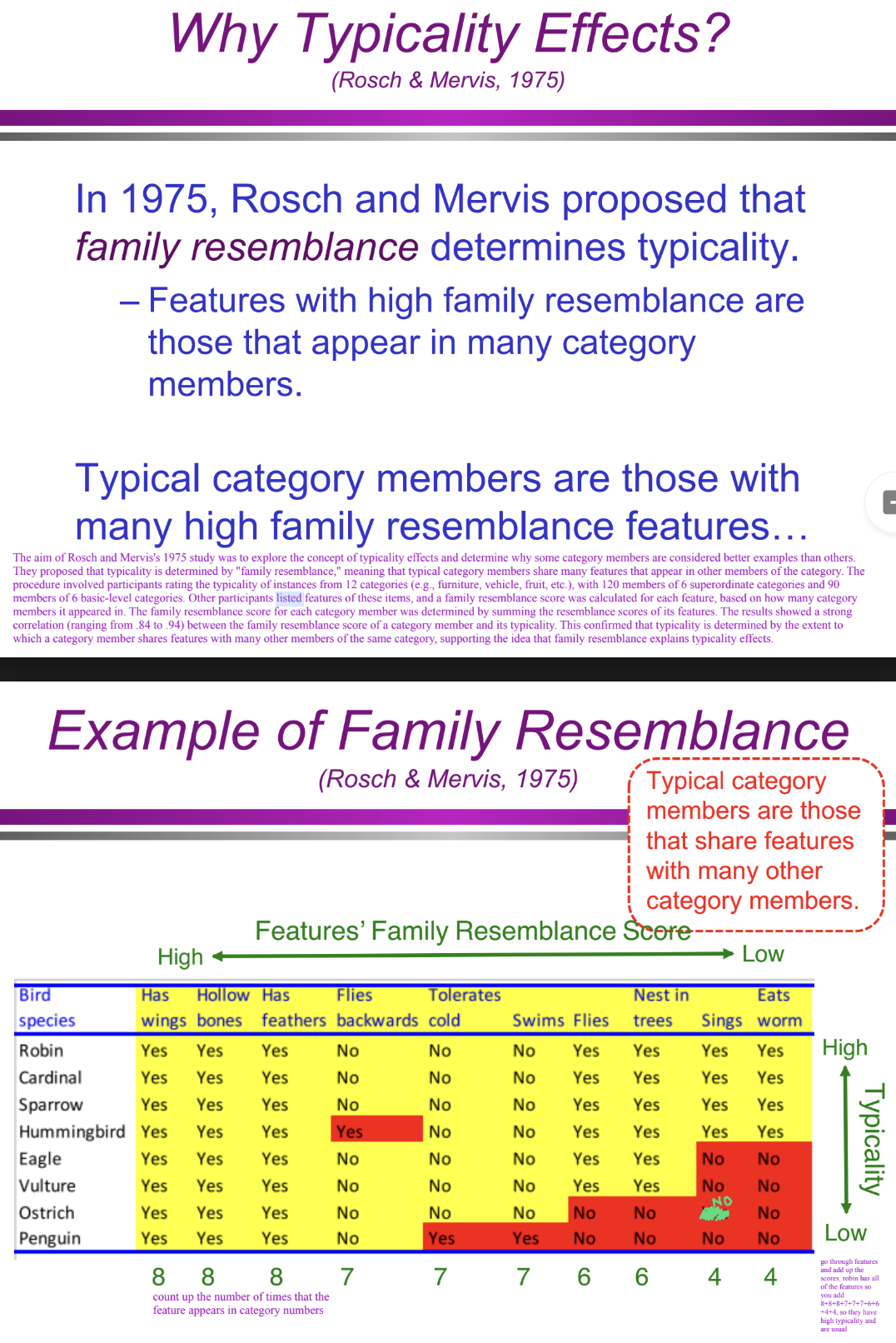
How does the example of family resemblance explain typical category members? (Categorization/Conceptual Structure: definitional approach)

• Typical category members (e.g., a robin as a bird) share many features with other members of the category.

• Atypical members (e.g., a penguin as a bird) share fewer features with other category members.

• For example, a robin has many high family resemblance features (e.g., small size, flies, sings, has feathers), while a penguin lacks some of these (e.g., it does not fly).

• The more shared features an item has, the higher its typicality score.

How did Wittgenstein explain family resemblance? (Categorization/Conceptual Structure: definitional approach)

Wittgenstein (1953) argued that categories do not have a single defining feature but are instead connected by a network of overlapping similarities. Using "games" as an example, he showed that board games, card games, and sports do not share one common trait, yet they form a category through shared but non-universal features like competition, rules, and entertainment.

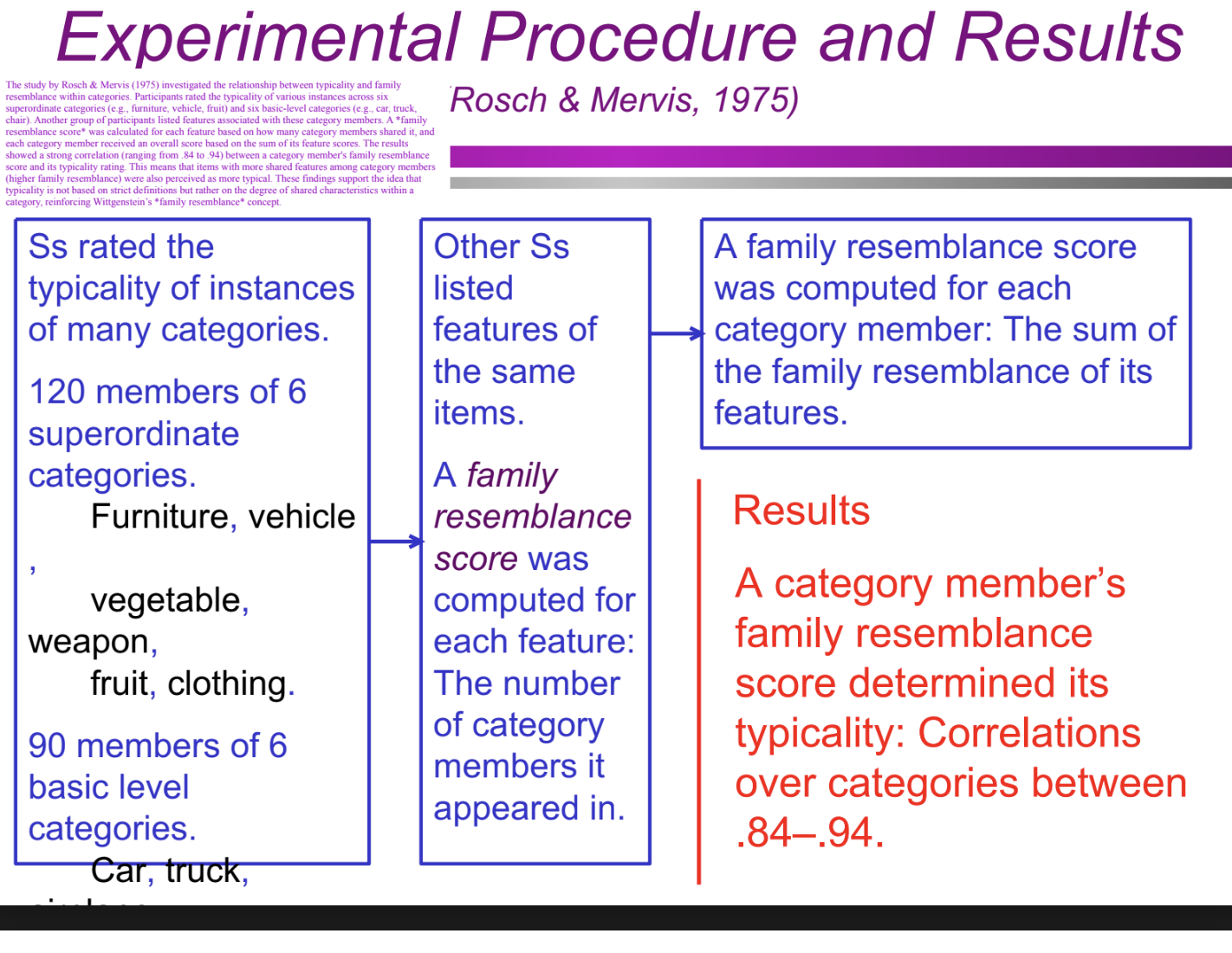
What were the steps in Rosch & Mervis’s (1975) study? (Categorization/Conceptual Structure: definitional approach)

1. Participants rated the typicality of items from six superordinate categories (e.g., furniture, vehicle, fruit) and six basic-level categories (e.g., car, truck, chair).

2. A second group listed features of these category members.

3. A family resemblance score was calculated for each feature, based on how many members of the category shared it.

4. A total family resemblance score was assigned to each category member by summing the scores of its features.

5. Researchers correlated typicality ratings with family resemblance scores to test their relationship.

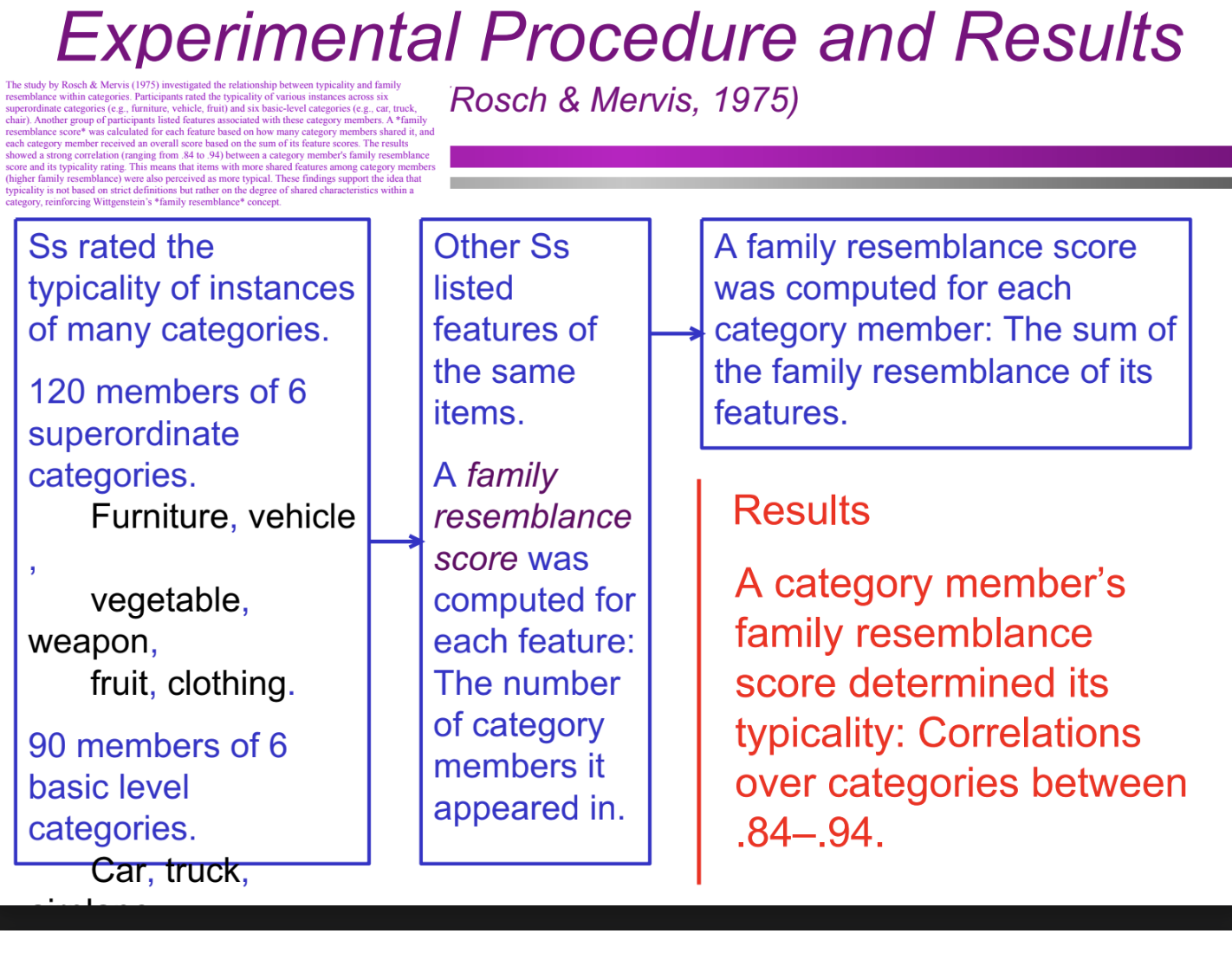
What were the key results of Rosch & Mervis’s (1975) study? (Categorization/Conceptual Structure: definitional approach)

The study found a strong correlation (ranging from .84 to .94) between family resemblance scores and typicality ratings. This means:

• The more features an item shared with other category members, the more typical it was judged.

• Items with lower family resemblance scores were rated as less typical.

• These findings support the idea that typicality is based on shared features rather than strict definitions, reinforcing the concept of graded category membership.

What are the problems of the definitional approach when applied to everyday categories? (Categorization/Conceptual Structure: definitional approach summary)

The definitional approach struggles with everyday categories because:

• No clear defining features: Many categories lack strict necessary and sufficient conditions.

• Borderline cases: Some items do not fit neatly into a category (e.g., is a tomato a fruit or vegetable?).

• Typicality effects: Some members are seen as better examples than others, suggesting categories are graded rather than strictly defined.

When do definitions work well for categorization? (Categorization/Conceptual Structure: definitional approach summary)

Definitions apply well to man-made categories, such as:

• Mathematical concepts (e.g., a triangle has three sides).

• Kinship terms (e.g., an uncle is the brother of a parent).

• Sports rules (e.g., a baseball strike has a precise definition).
  Unlike natural categories, these are often created with clear-cut definitions in mind.

What are probabilistic/similarity-based views of categorization? (Categorization/Conceptual Structure: probabilistic/similarity based views)

These views suggest that category membership is determined by similarity rather than strict definitions. Two main models include:

• Prototype models: Categories are represented by an idealized, central prototype.

• Exemplar models: Categories are represented by specific examples from experience.

What is prototype theory, and what are its two key components? (Categorization/Conceptual Structure: prototype theory)

Prototype theory states that categories have a probabilistic structure, meaning membership is based on similarity rather than strict definitions. It has two main components:

1. Learning by prototype abstraction: Forming an idealized mental representation based on shared features of category members.

2. Classification by similarity to the prototype: New items are categorized based on their resemblance to this prototype.

What is a probabilistic structure in categorization? (Categorization/Conceptual Structure: prototype theory)

A probabilistic structure means that category membership is not absolute but based on the likelihood of an item sharing features with other category members. Some items are better examples than others, leading to graded category membership.

What is a prototype in prototype theory? (Categorization/Conceptual Structure: prototype theory)

A prototype is an idealized, abstract representation of a category that captures the most common or typical features shared by category members. Items are classified based on their similarity to this prototype.

What is multidimensional space in categorization? (Categorization/Conceptual Structure: prototype theory)

A multidimensional space is a way to represent category members based on multiple features (e.g., size, color, shape). Items that are closer in this space are more similar, while items that are farther apart are more dissimilar.

How do multidimensional spaces help represent categorization? (Categorization/Conceptual Structure: prototype theory)

They allow us to visualize similarity as distance, where:

• Nearby objects are more similar.

• Distant objects are more dissimilar.
  This helps explain graded membership and why some category members feel more typical than others.

What is the first component of prototype theory (learning by prototype abstraction)? (Categorization/Conceptual Structure: prototype theory)

Learning by prototype abstraction involves averaging all observed category members' features across various dimensions to form a mental prototype.

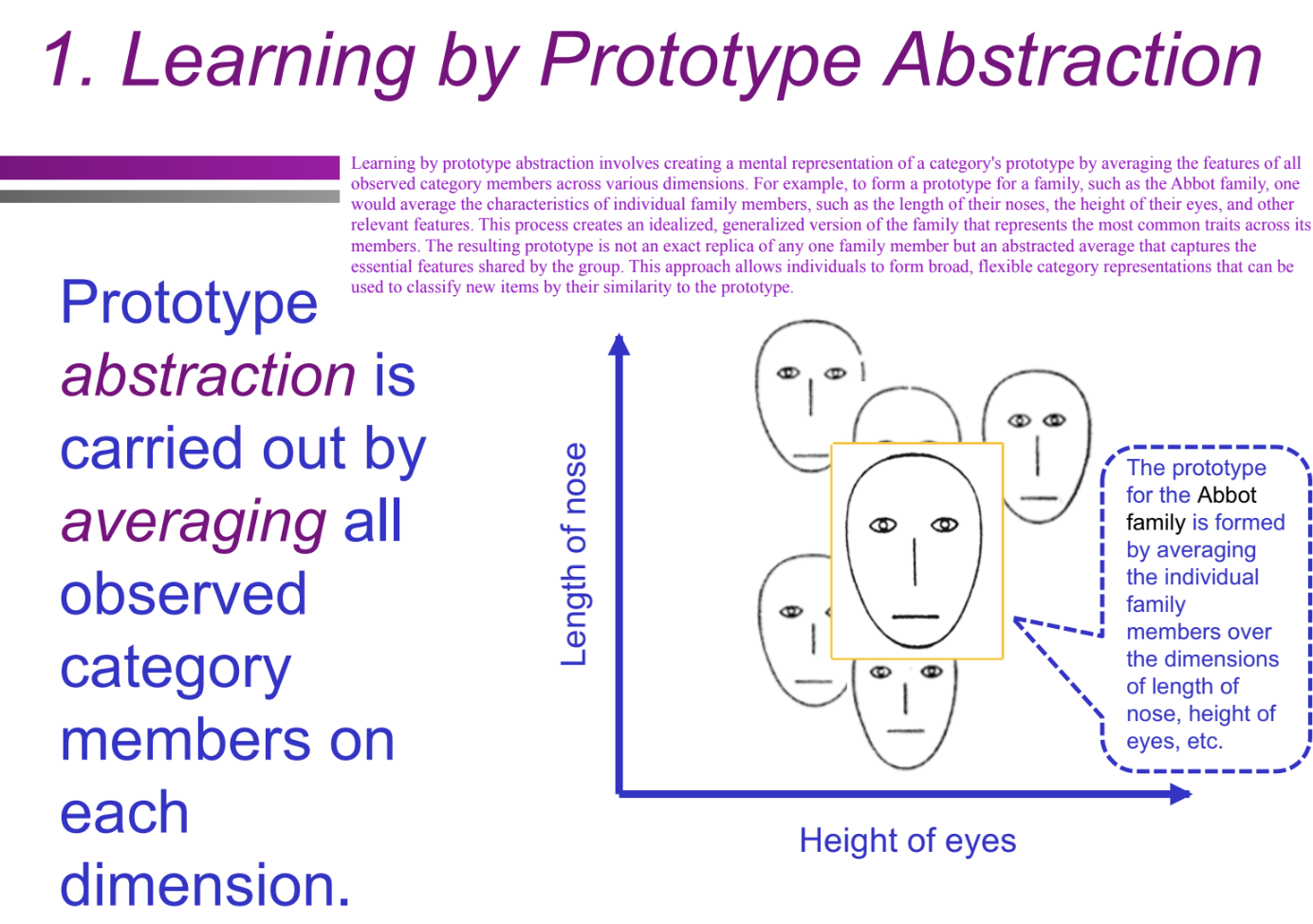
What is abstraction in prototype learning? (Categorization/Conceptual Structure: prototype theory)

Abstraction is the process of creating a generalized mental representation by extracting common features from multiple category members while ignoring minor variations.

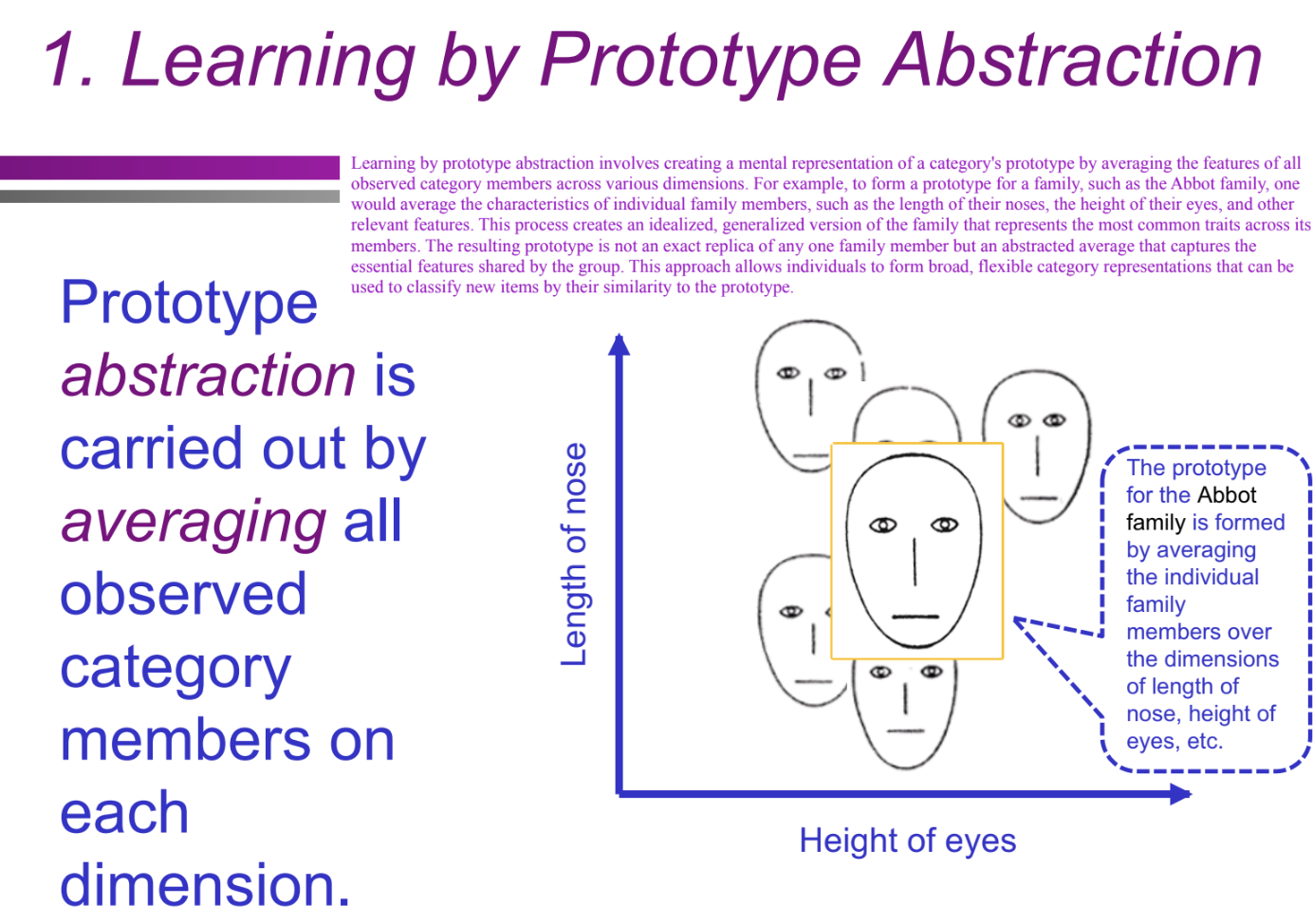
What is averaging in prototype abstraction? (Categorization/Conceptual Structure: prototype theory)

Averaging is the process of calculating the mean of observed features across category members to create an idealized prototype.

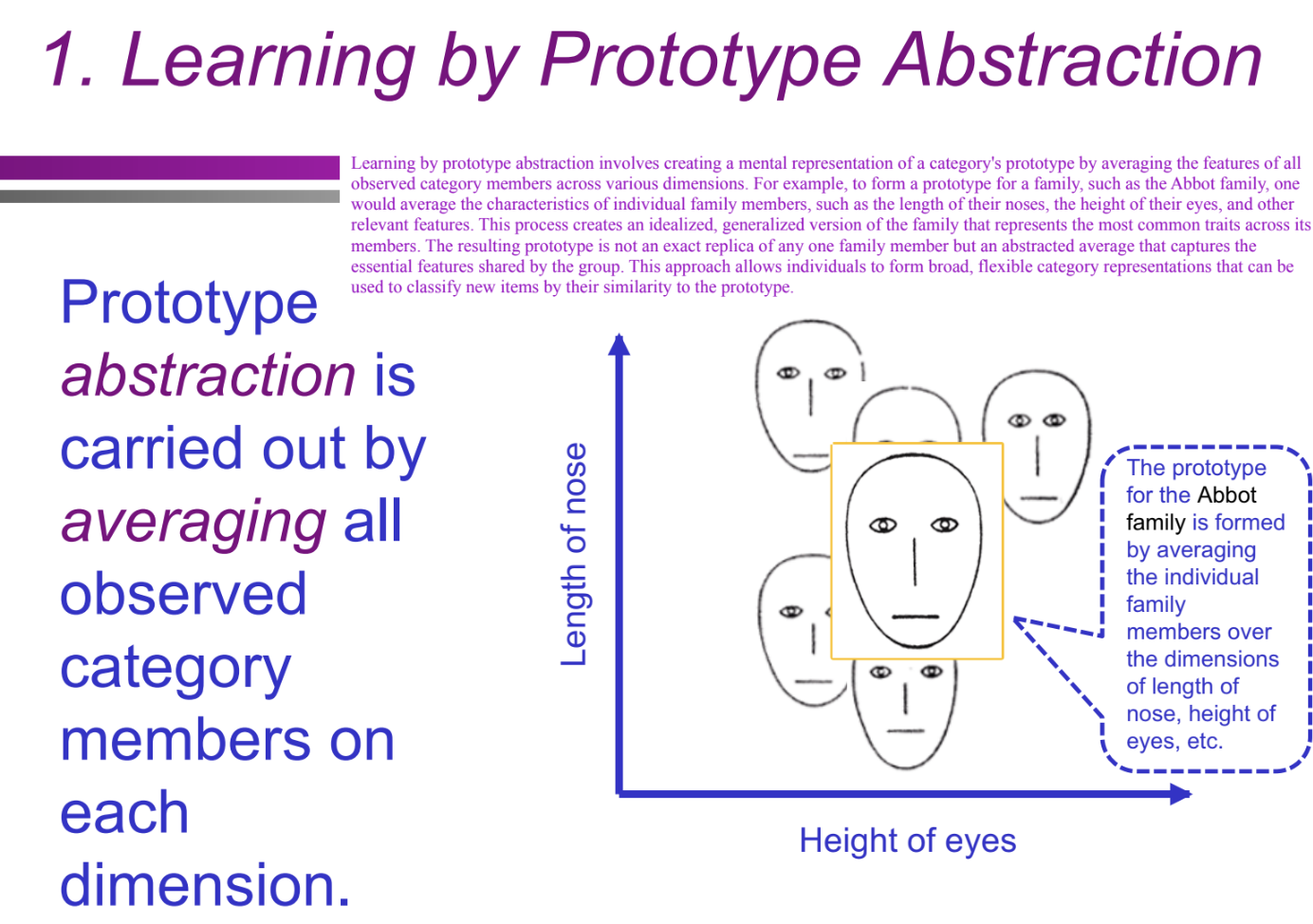
How does the Abbot family example illustrate learning by prototype abstraction? (Categorization/Conceptual Structure: prototype theory)

A prototype of the Abbot family is formed by averaging traits like nose length and eye height across family members. This results in a generalized family prototype rather than a copy of any one individual.

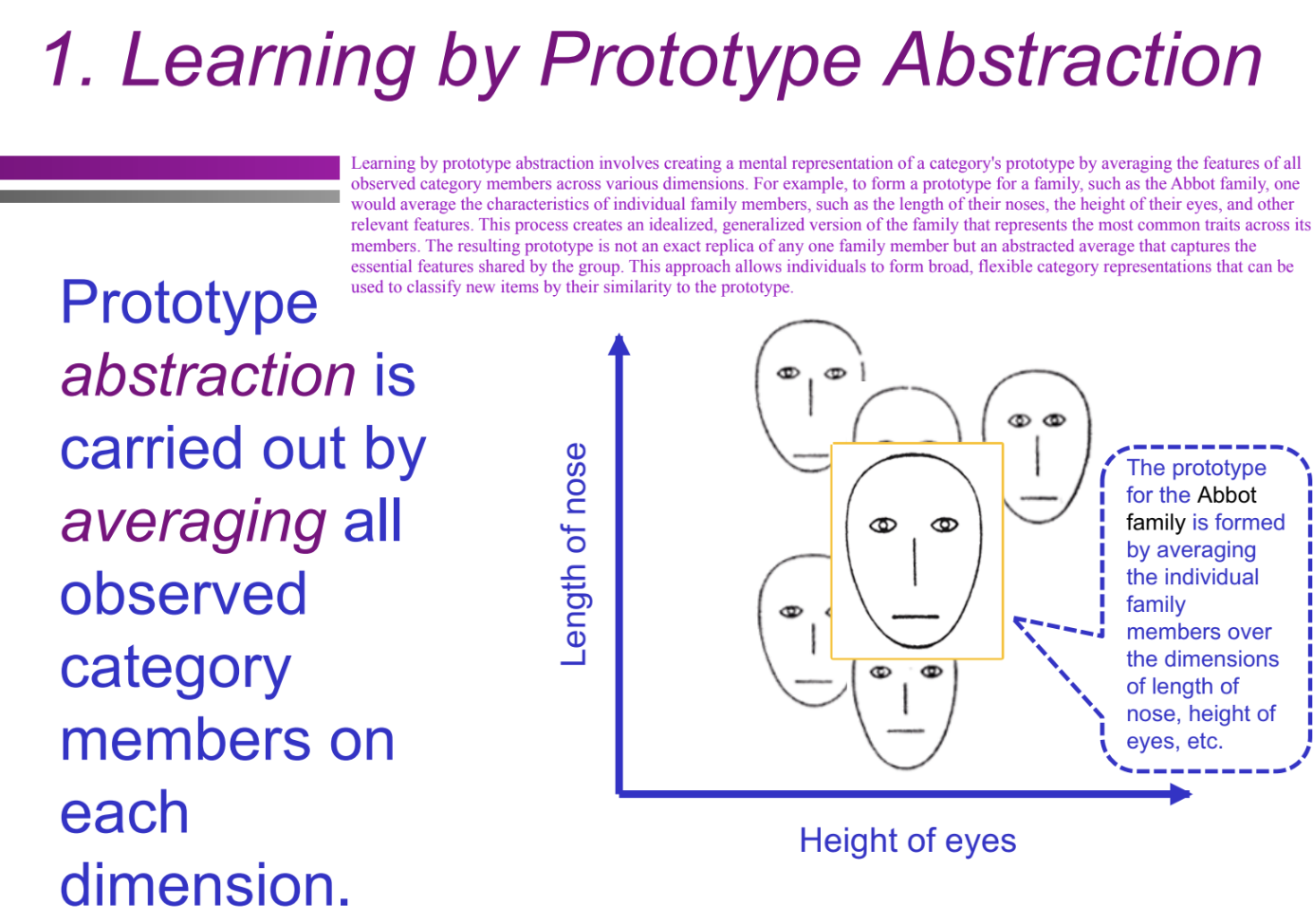
What is the second component of prototype theory (classification by similarity)? (Categorization/Conceptual Structure: prototype theory)

Classification by similarity means that new objects are categorized based on their similarity to existing prototypes, measured by their distance in psychological space.

What is similarity in prototype classification? (Categorization/Conceptual Structure: prototype theory)

Similarity refers to how close an object is to a prototype in psychological space, with closer objects being more likely to belong to that category.

How does the Abbot family example illustrate classification by similarity? (Categorization/Conceptual Structure: prototype theory)

A new face is classified as an Abbot if it is closer (more similar) to the Abbot prototype than to the prototype of another family, such as the Bakers.

How does the dog vs. fish vs. chair example illustrate classification by similarity? (Categorization/Conceptual Structure: prototype theory)

If an object (A) has features closer to the dog prototype, it is classified as a dog. If object (B) is more similar to the fish prototype, it is classified as a fish, and if object (C) is closest to the chair prototype, it is classified as a chair.

How does prototype theory connect to memory? (Categorization/Conceptual Structure: prototype theory)

Prototype theory suggests that memory operates efficiently by accessing all prototypes in parallel when classifying new objects. This allows for quick classification without consciously recalling each prototype individually.

What are the advantages of prototype theory? (Categorization/Conceptual Structure: prototype theory)

Prototype theory explains key phenomena such as typicality effects, borderline cases, and the absence of defining features in categories. It accounts for flexibility in categorization, with category membership based on similarity to prototypes rather than rigid definitions.

How does prototype theory explain typicality and borderline cases? (Categorization/Conceptual Structure: prototype theory)

In prototype theory, typicality effects occur when objects like robins are closer to the prototype of a category, while atypical items like penguins and ostriches are farther away.

Borderline cases are objects, like cats vs. penguins, that are equidistant from two or more prototypes, making their classification unclear.

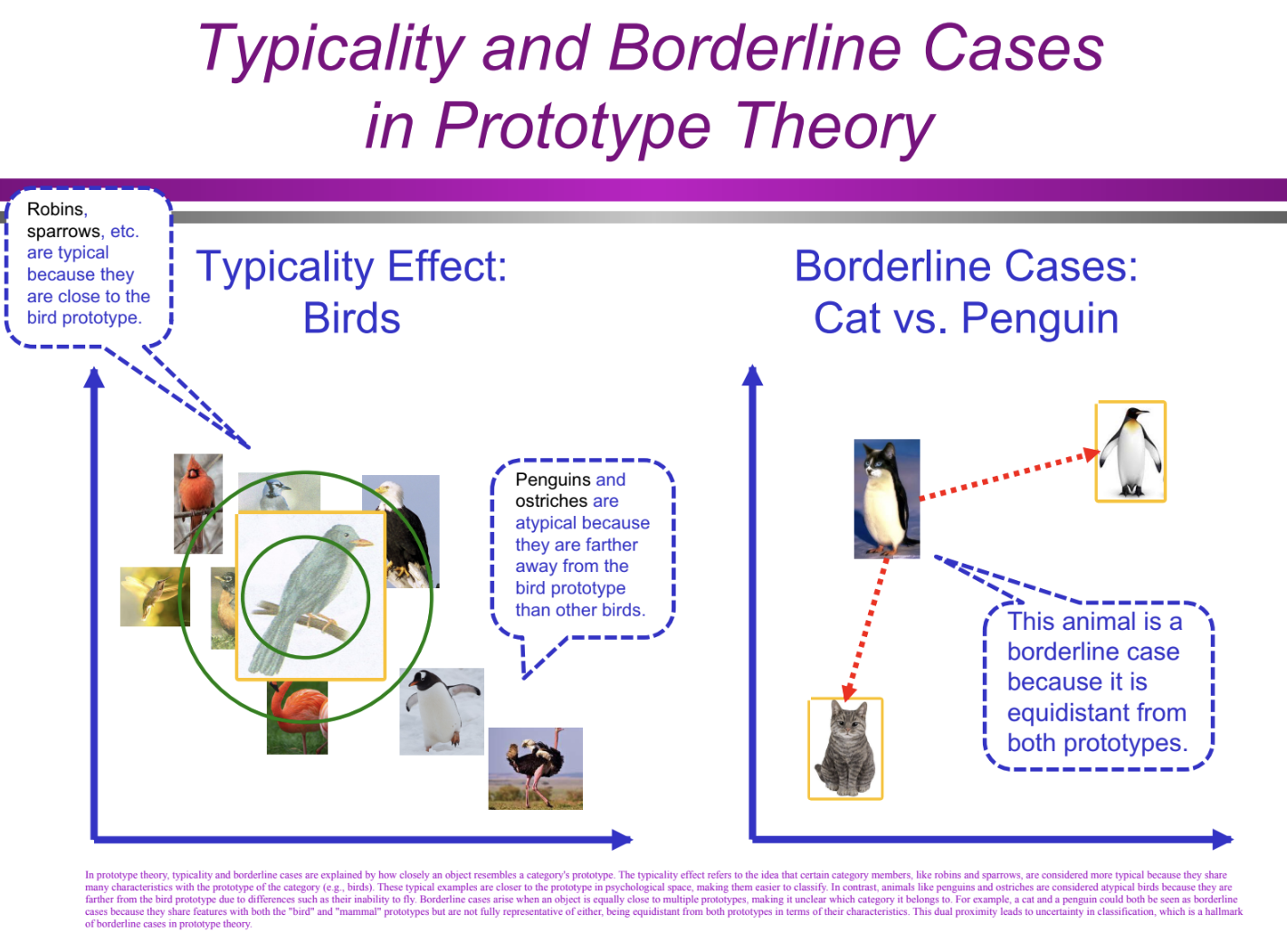
What are some empirical phenomena that support prototype theory? (Categorization/Conceptual Structure: prototype theory)

Evidence for prototype theory includes the fact that typical objects are listed first (e.g., robin before ostrich), typical objects are primed more strongly, and statements about typical objects are verified faster (e.g., "an apple is a fruit" > "a kiwi is a fruit").

Why is prototype theory considered a successful theory of categorization? (Categorization/Conceptual Structure: prototype theory)

Prototype theory is successful because it accounts for key empirical results such as no defining features, typicality effects, borderline cases, and statement verification times. It offers a flexible and intuitive explanation for how we categorize objects.