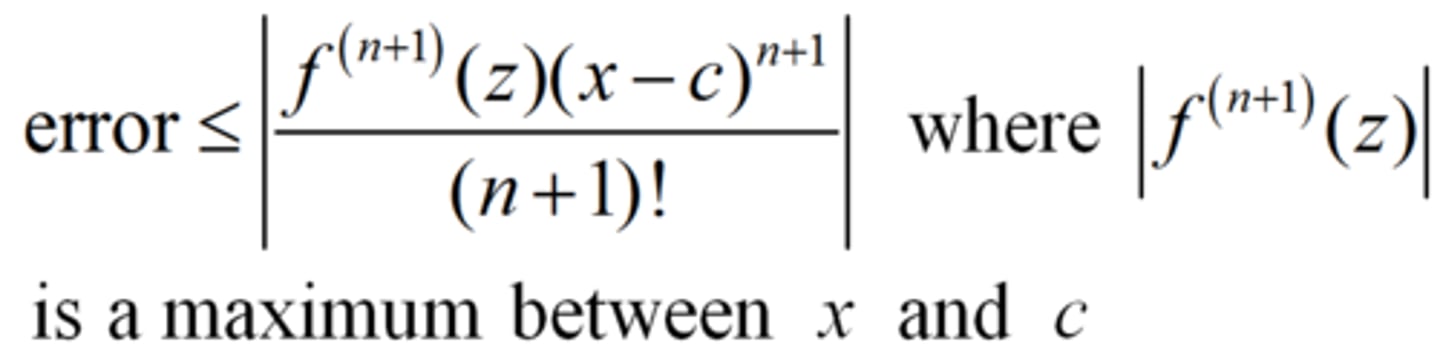AP Calculus BC Review

Tangent Line

Straight line on the curve at a given point that can be used to estimate values near by

Slope

Rise over run

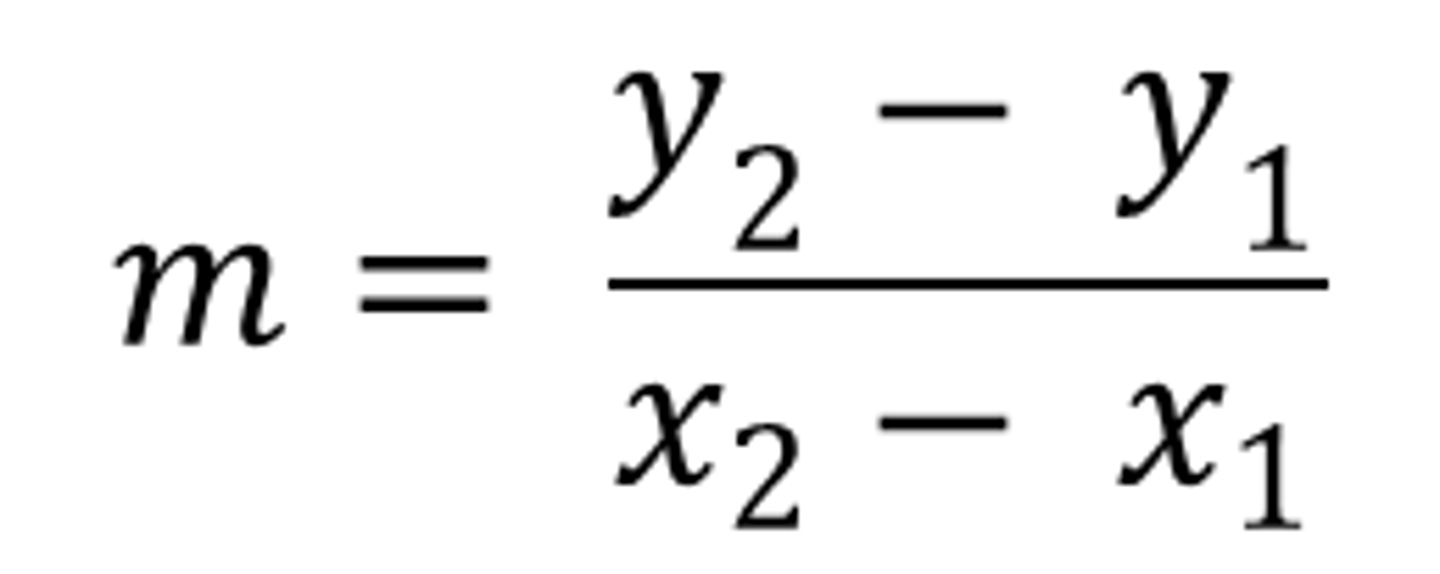
Instantaneous Rate of Change

the rate of change at a particular moment, for F(x) this would be F'(x)

Average Rate of Change

the change in the value of a quantity divided by the elapsed time

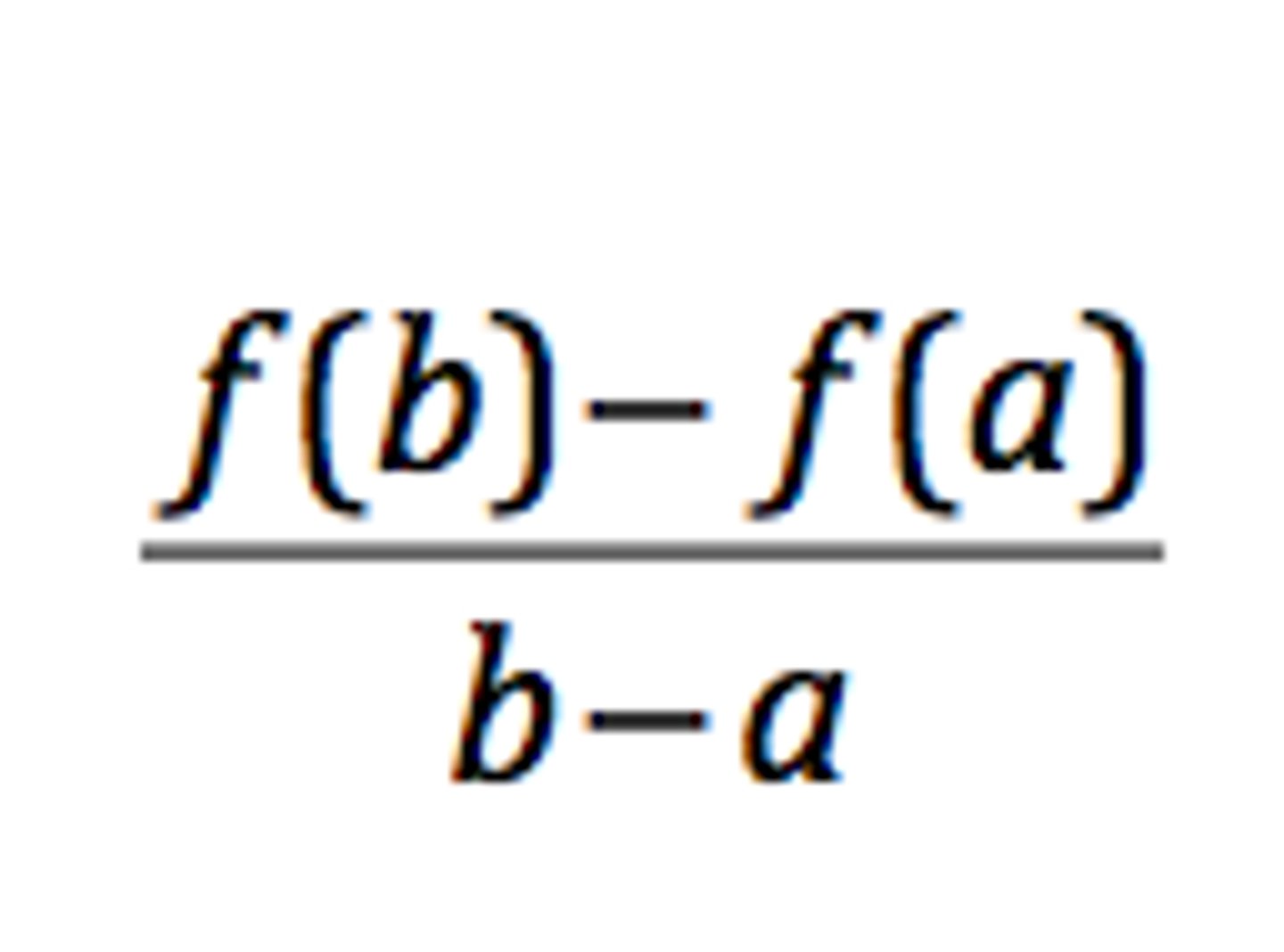
Average Value

finds the average value of a function. often related to the mean value theorem

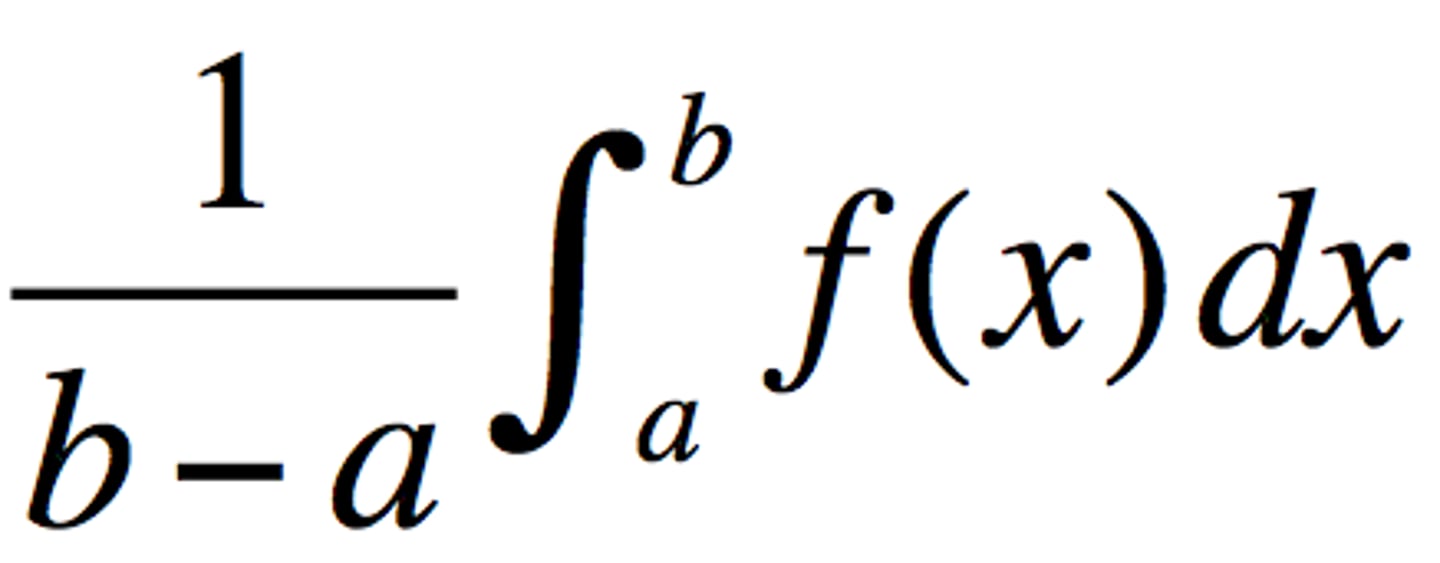
Linear Approximation

Using the tangent line to approximate nearby values

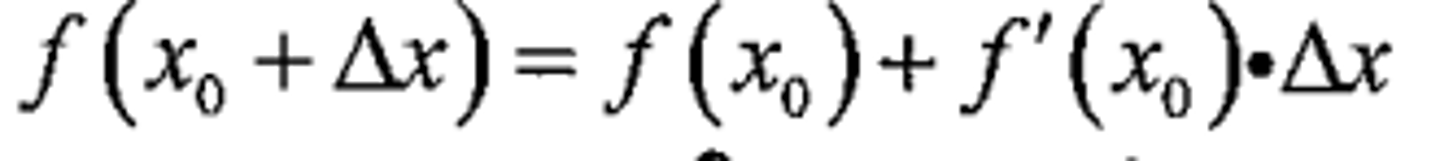
Displacement

The distance and direction of an object's change in position from the starting point.

function is given in relation to time

Velocity

The speed at which an object is traveling

velocity function is the derivative of a position function in relation to time.

Acceleration

The rate at which velocity changes

Acceleration function is the derivative of a velocity function in relation to time

Total Distance

Total distance traveled

to do this calculate integral of velocity graph positive and negative sections separately and add absolute value of those together.

Speeding Up

Acceleration has the same sign as Velocity

Slowing Down

Acceleration has the opposite sign as Velocity

Area Under the Curve

Integral or antiderivative

Area Between Curves

with f(x) on top and g(x) on bottom

a and b represent bounds or where the two graphs intersect

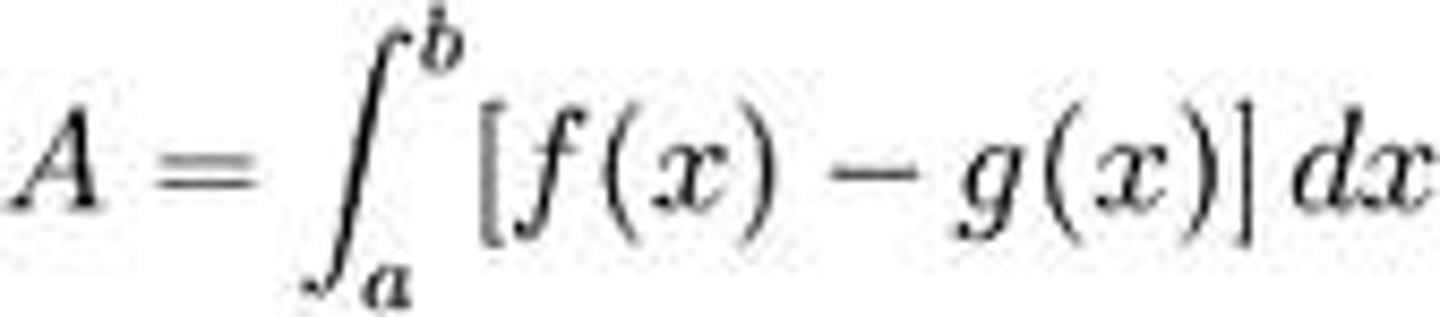
Disc Method of Rotation

V = pi * int from a to b of R(x)^2 dx

R(x) is radius and dx is height

rotated around variable inside

Washer Method of Rotation

V = pi * int from a to b of ( R(x)^2 - r(x) ^2 ) dx

R(x) is furthest away from axis

r(x) is closest to axis

rotated around variable inside

Shell Method of Rotation

V = 2pi int from a to b of ( x F(x) ) dx

rotated around opposite variable inside

Definition of A Derivative

we say that f is differentiable at x = a and the limit is the derivative of f(x) at x = a, denoted by f prime of a.

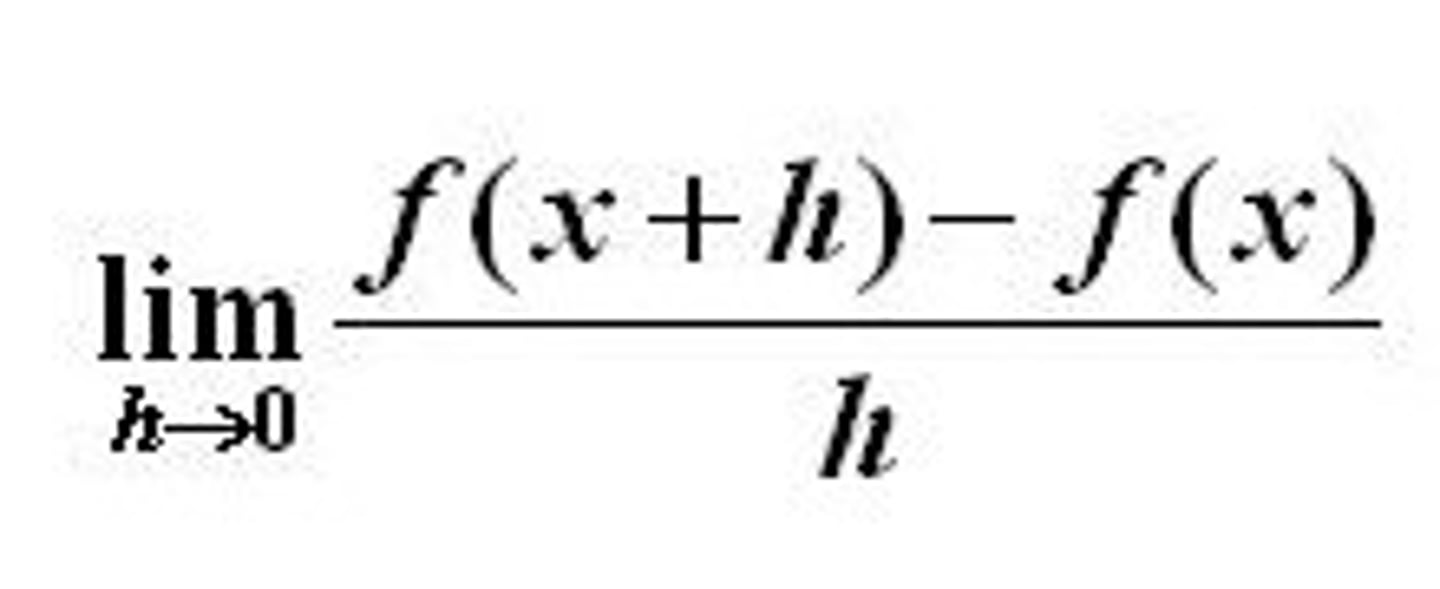
Continuity

A function is uninterrupted, this implies integratibility

Product Rule

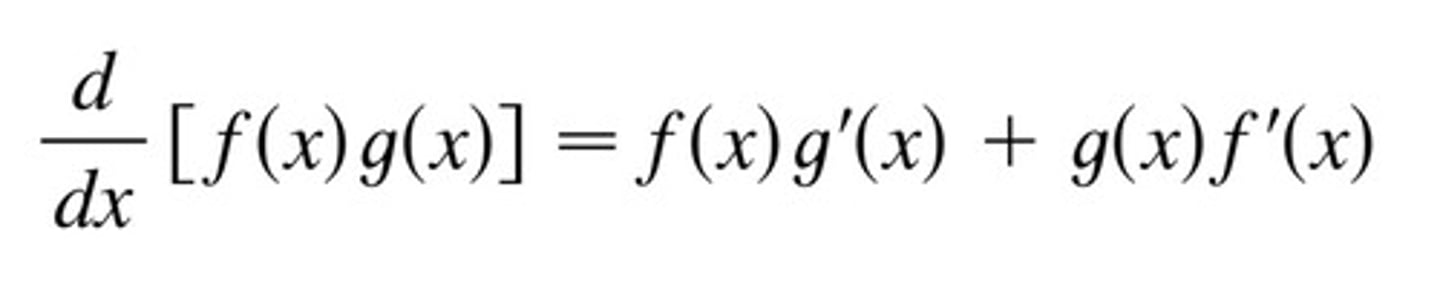
Quotient Rule

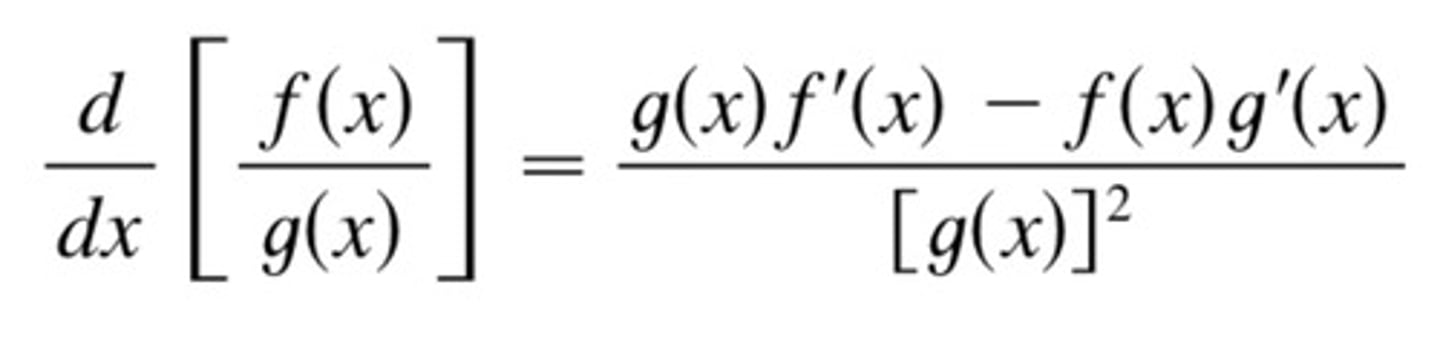
Chain Rule

also applies to Trig functions, natural logs, and e

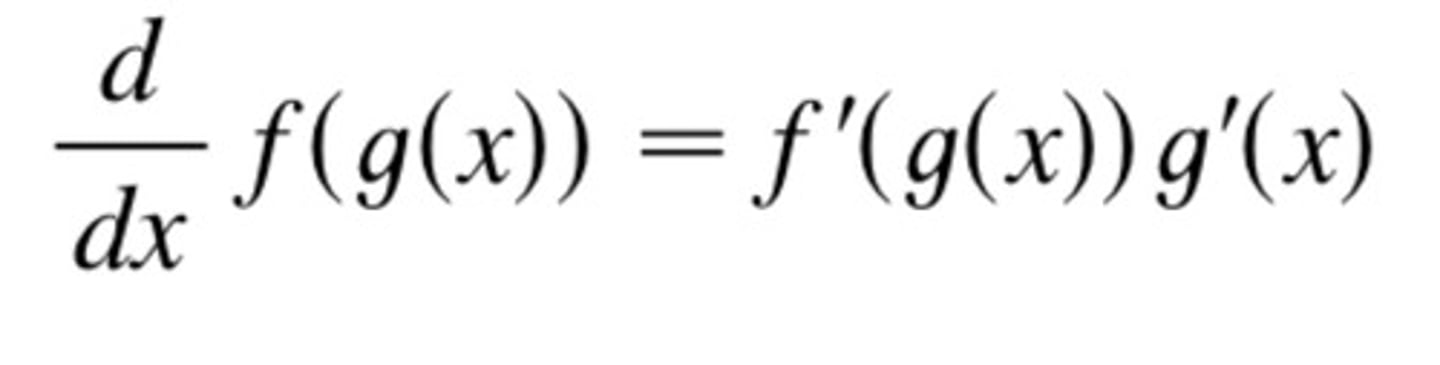
U-Substitution

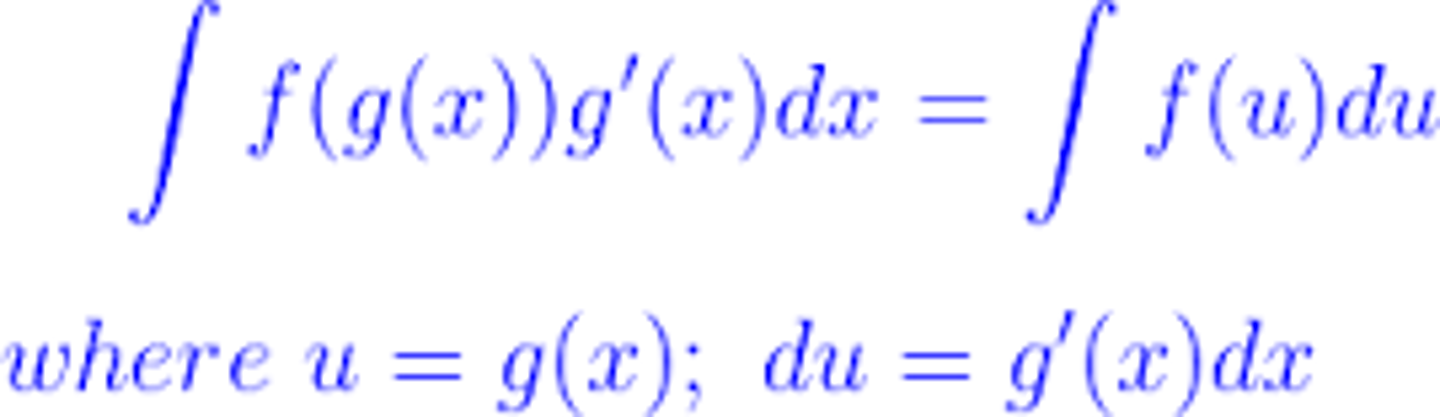
Integration by Parts

int u dv = u v - int v du

Partial Fractions

Splitting up a fraction into its parts can make integration easier!

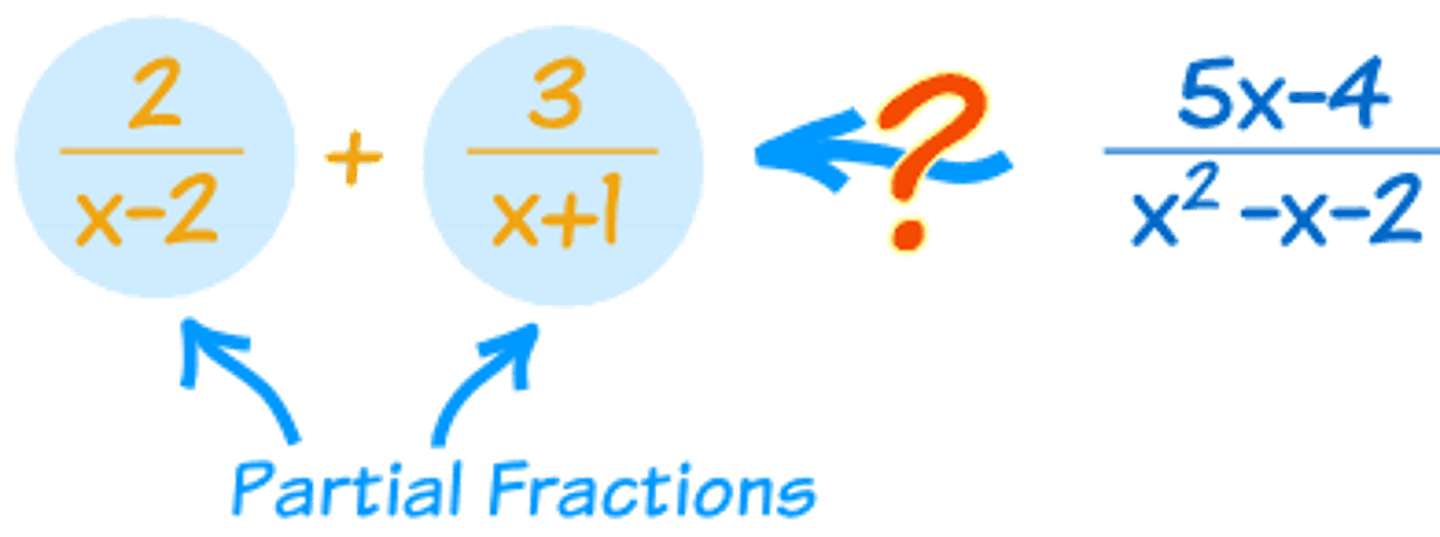
Slope Fields

Drawing the slopes at different points for a function (often that is difficult to integrate) can help predict the shape of the function

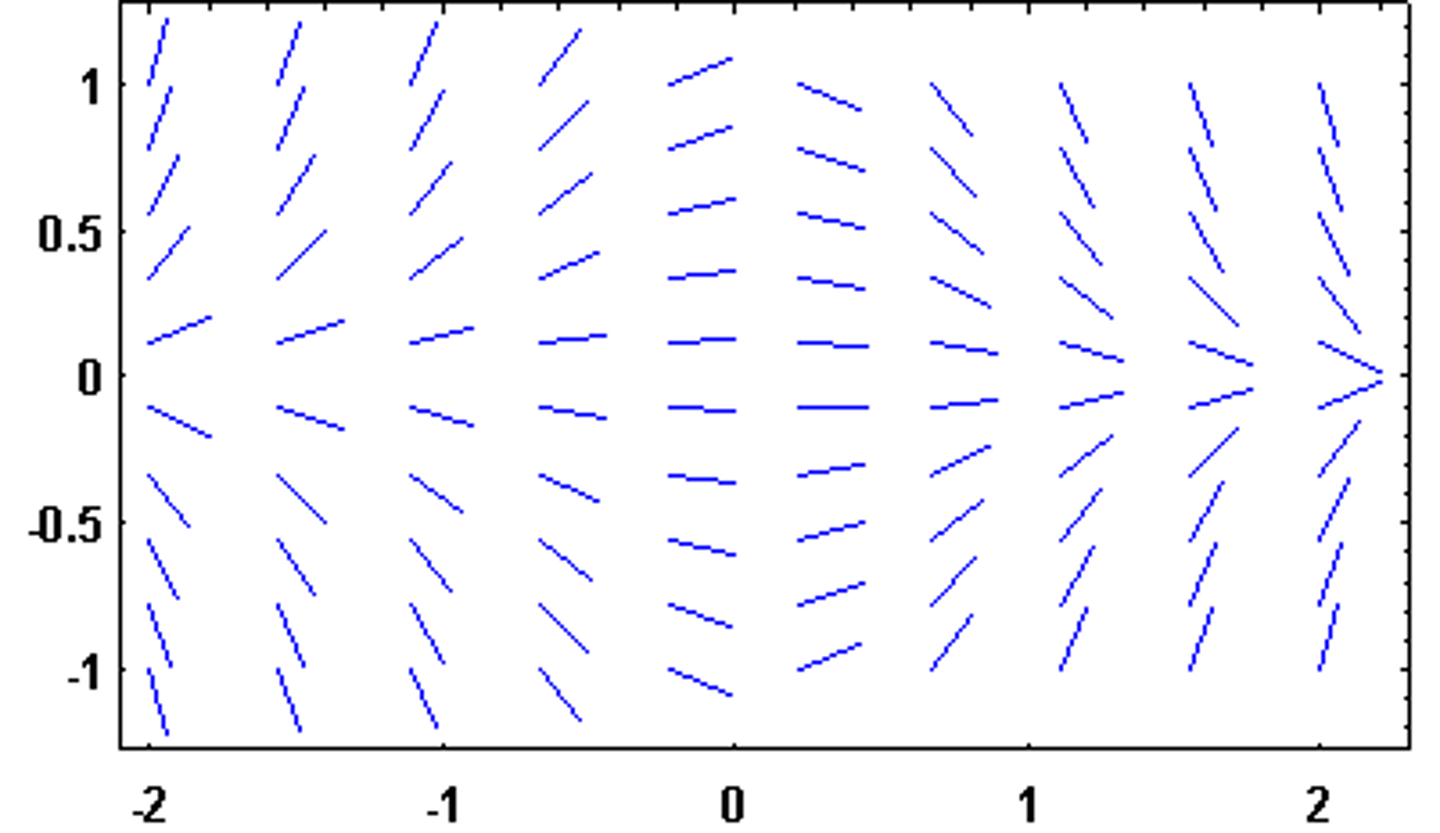
Particular Solution

Integration that has value for c solved for by plugging in a known coordinate pair

Euler's Method

a method of approximation helpful when dy/dx has x and y terms in it

g(x) is increasing

g'(x) is positive

g(x) is decreasing

g'(x) is negative

g(x) is concave up

g''(x) is positive

g(x) is concave down

g''(x) is negative

g(x) changes directions

g'(x) passes through 0

g(x) has a point of inflection

g''(x) passes through 0 or DNE

Local/Relative Maximum

A point on the graph of a function where no other nearby points have a greater y-coordinate.

Local/Relative Minimum

A point on the graph of a function where no other nearby points have a lesser y-coordinate.

Absolute Maximum

The y-value of a point on a graph that is higher than any of the other points on the entire graph.

Needs to be proved with critical points and the limits as x approaches - infinity and + infinity

Absolute Minimum

The lowest point of the function

Needs to be proved with critical points and the limits as x approaches - infinity and + infinity

Stationary Points

Maximum Points, Minimum Points, and Points of Inflection

Critical Point

Occurs when f'(x) = 0

Can be a min, max, or neither

Related Rates

A class of problems in which rates of change are related by means of differentiation. Standard examples include water dripping from a cone-shaped tank and a man's shadow lengthening as he walks away from a street lamp.

Riemann Sums

A Riemann Sum is a method for approximating integrals

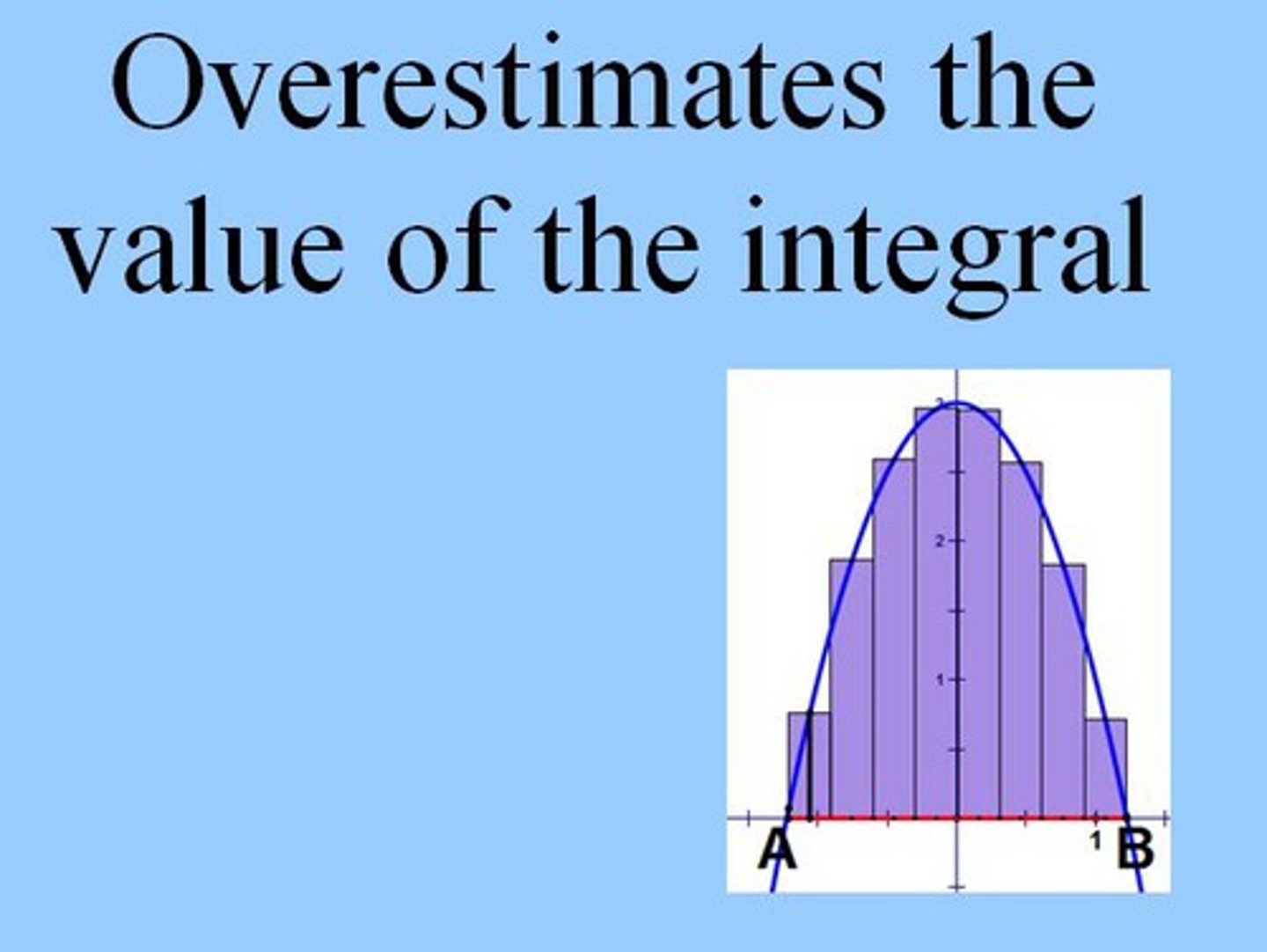
Trapezoidal Sums

Riemann Sums done with averaging two points instead of picking a side

can be more accurate

Mean Value Theorem

the average value on a certain integral must have a value of x that it is equal to

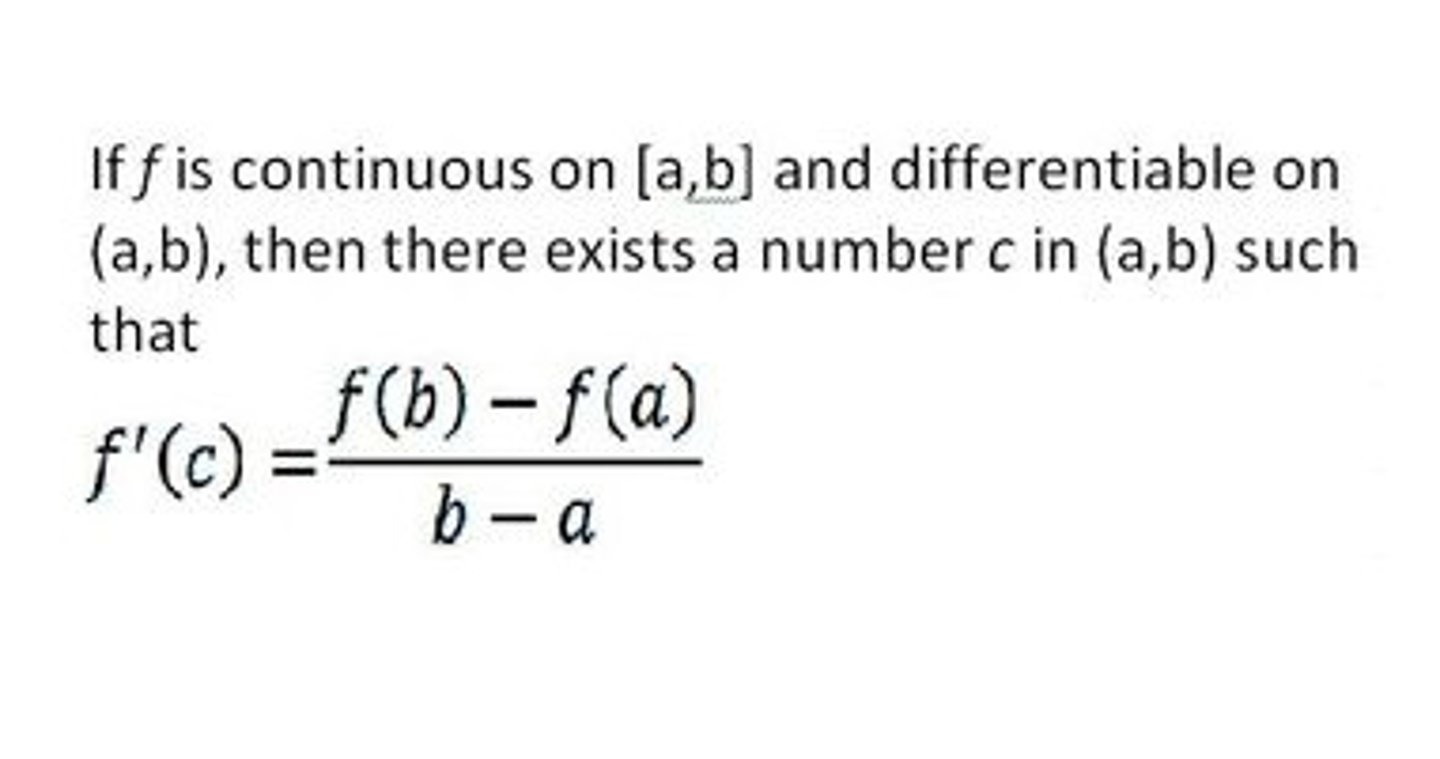
Intermediate Value Theorem

Extreme Value Theorem

1st Fundamental Theorem of Calc

int from a to b of f'(x) dx = f(b) - f(a)

2nd Fundamental Theorem of Calc

d/dx (int from c to x of f(t) dt) = f(x)

L'Hopital's Rule

if lim x --> of g(x)/f(x) is 0/0 then you can derive

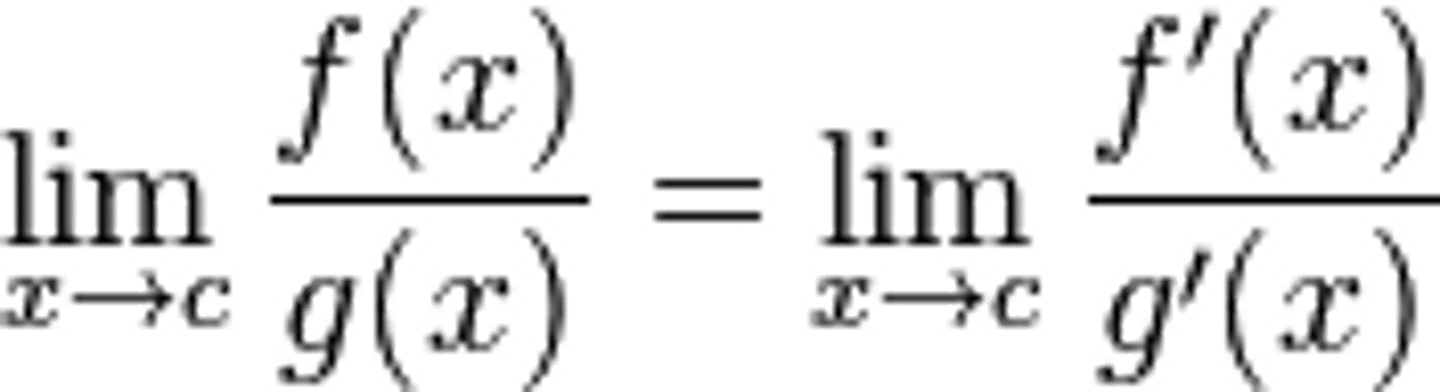
Find int 0 to infinity of f(x) dx

substitute b and do lim as b--> infinity

Polar Coordinates

(r,theta)

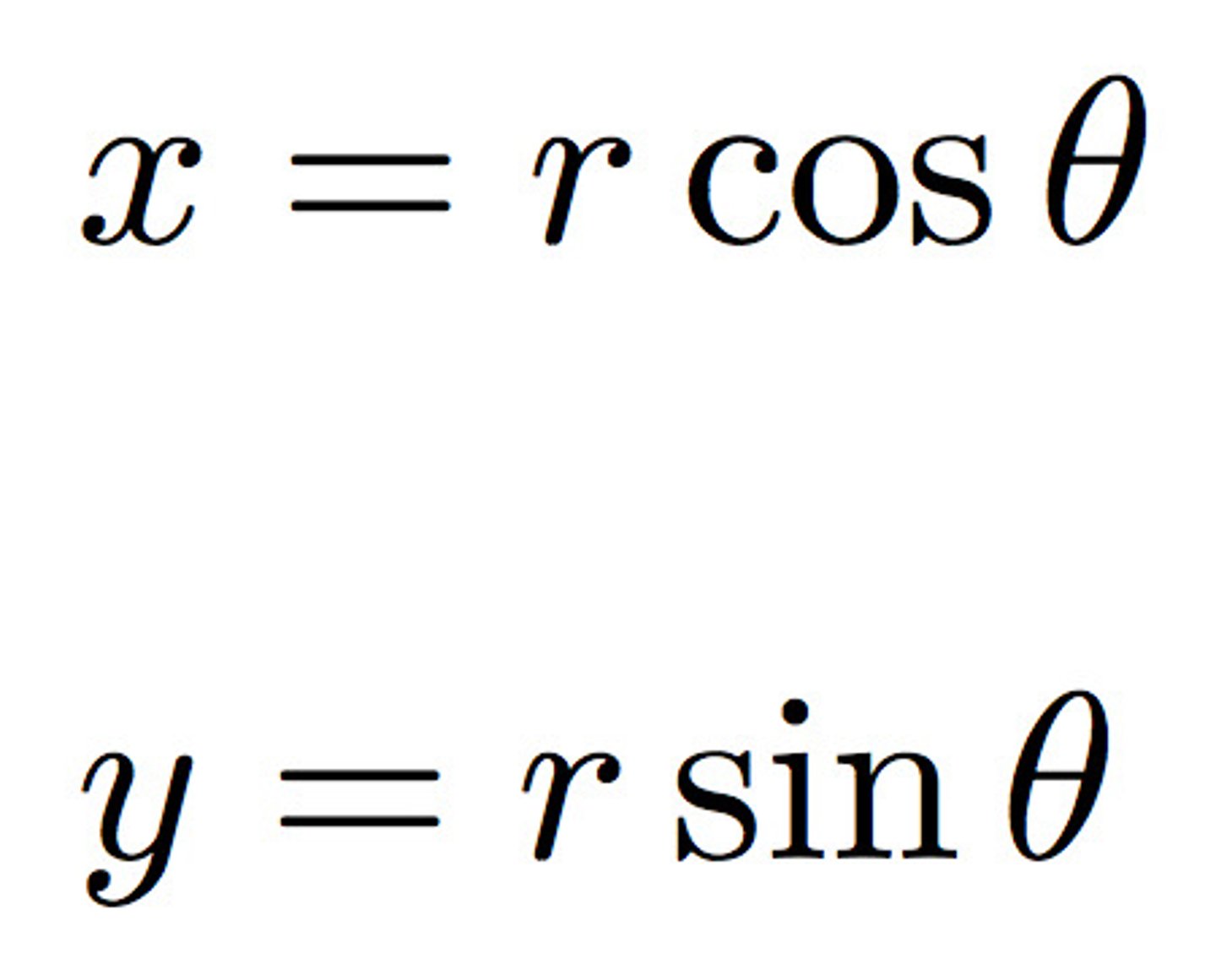
Polar Derivatives

dy/dx = (dy/dtheta)/(dx/dtheta)

Polar Length of Curve

int of alpha to beta of sqrt ( (dx/dtheta)^2 + (dy/dtheta)^2)

Polar Integrals

0.5 int from alpha to beta r^2 dtheta = area

Parametric Coordinates

(x(t),y(t))

Parametric Derivatives

dy/dx = (dy/dt)/(dx/dt)

d2y/dx2 = (d/dt(dy/dt))/(dx/dt)

Parametric Length of Curve

int of a to b of sqrt ( (dx/dt)^2 + (dy/dt)^2)

Parametric Integrals

integrals normal but with position vectors and relative to t

Particle motion

s = ( x(t) , y(t) )

v = ( x'(t), y'(t) )

a = ( x''(t), y''(t) )

Magnitude

|| v(t) || = sqrt ( ((dx/dt)^2) + ((dy/dt)^2) )

Series for sin x

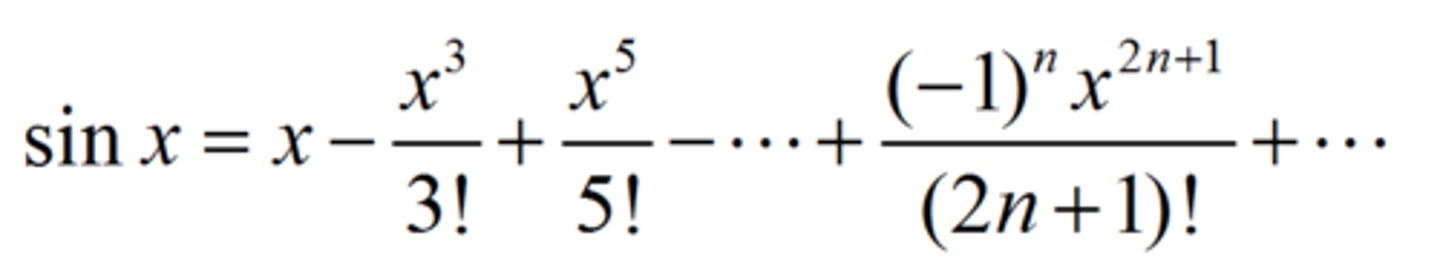
Series for cos x

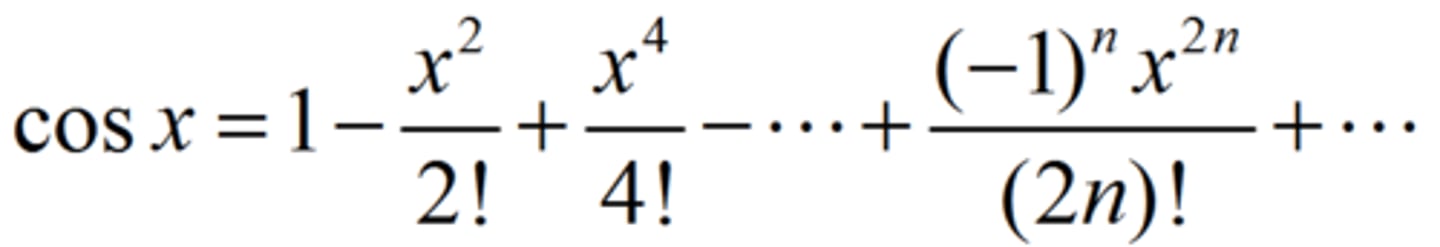
series for e^x

e^x = 1 + x + (x^2)/2! + (x^3)/3! + ...

Maclaurin Series

a Taylor series about x=0

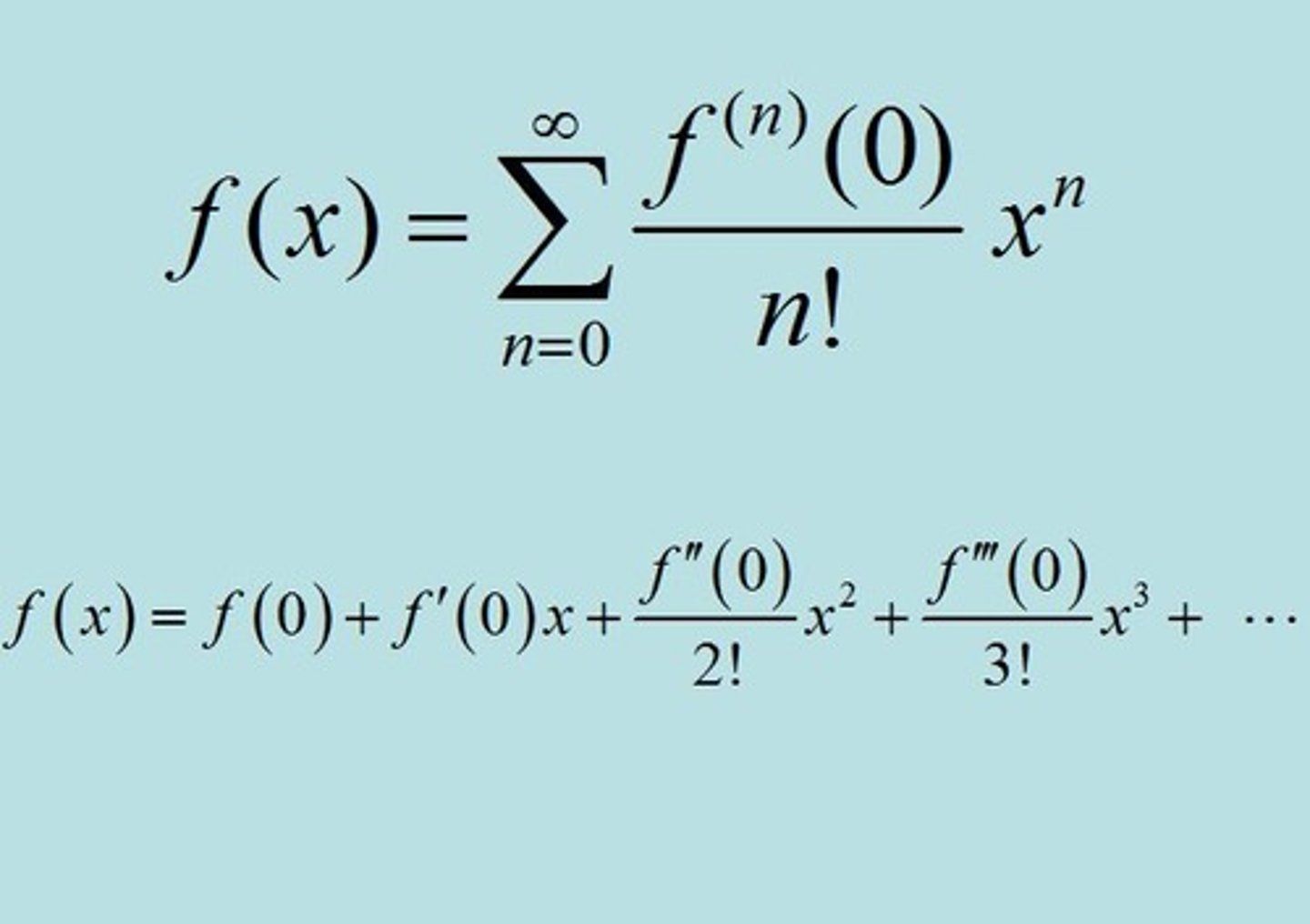
Taylor Series

if the function f is smooth at x=a, then it can be approximated by the nth degree polynomial f(x) ~ f(a) + f'(a)(x-a) + f"(a)(x-a)^2/2! + ... + f^n(a)(x-a)^n/n!

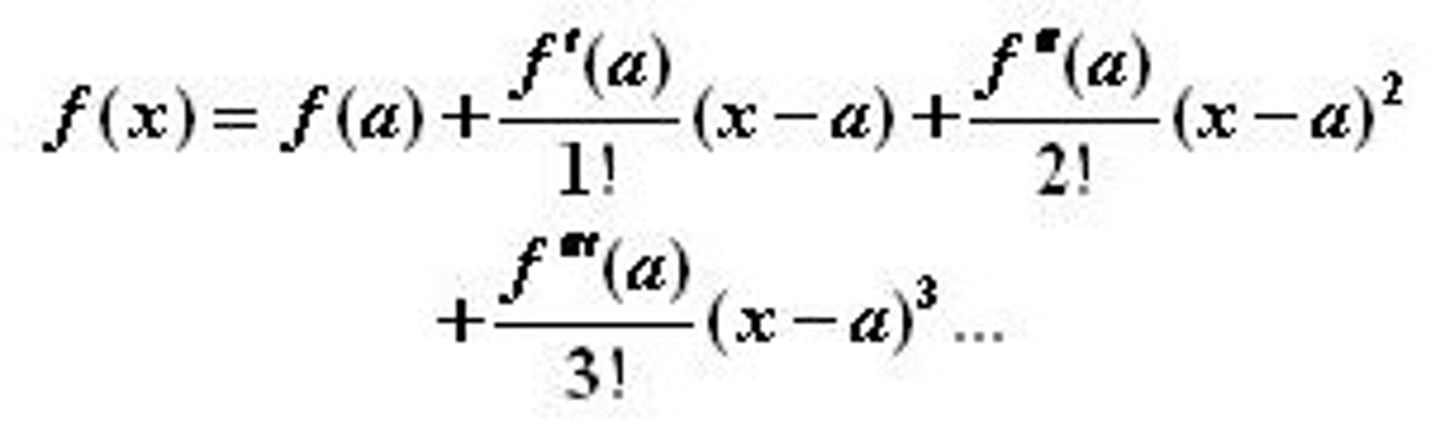
nth term test for divergence

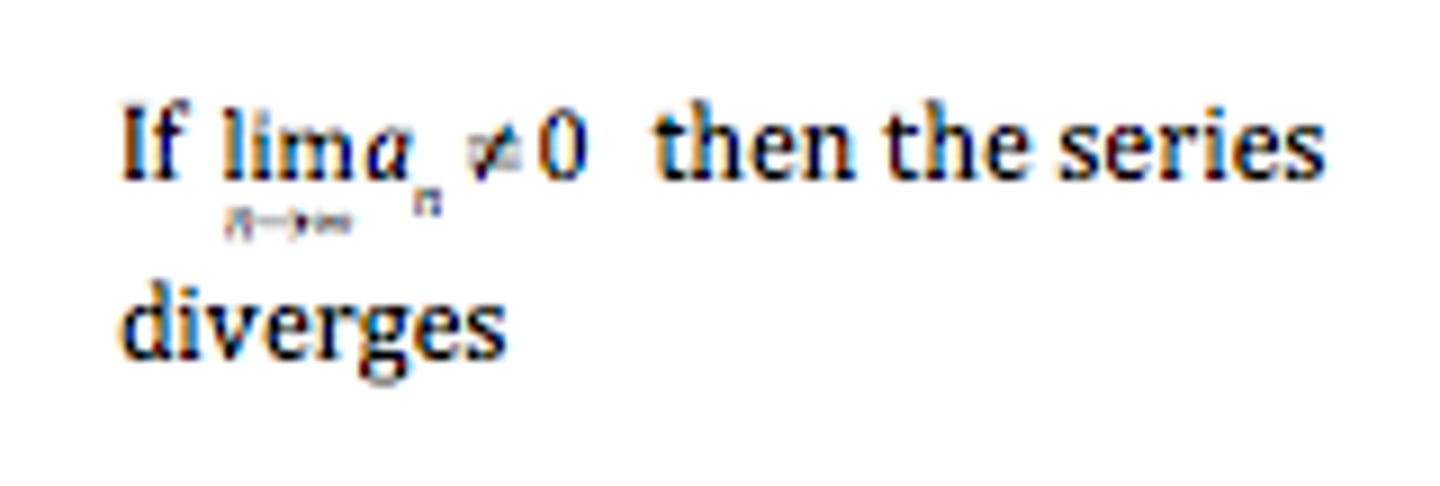
p-series test

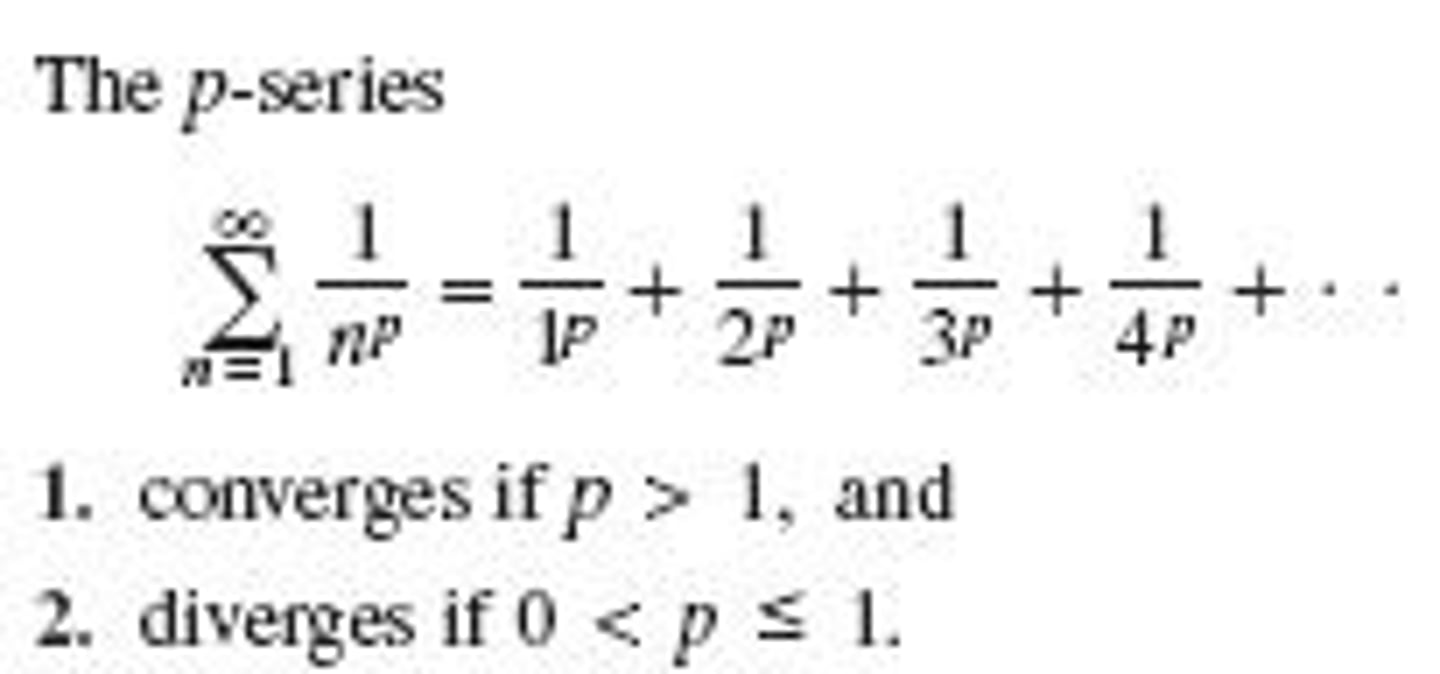
Geometric Series Test

An = a r^(n-1) , n>= 1

|r| < 1 converges to a/(1-r)

Alternating Series Test

An = (-1)^n bn , bn>=0

is bn+1 <= bn and lim n-> infinity of bn=0 series converges

Direct Comparison Test

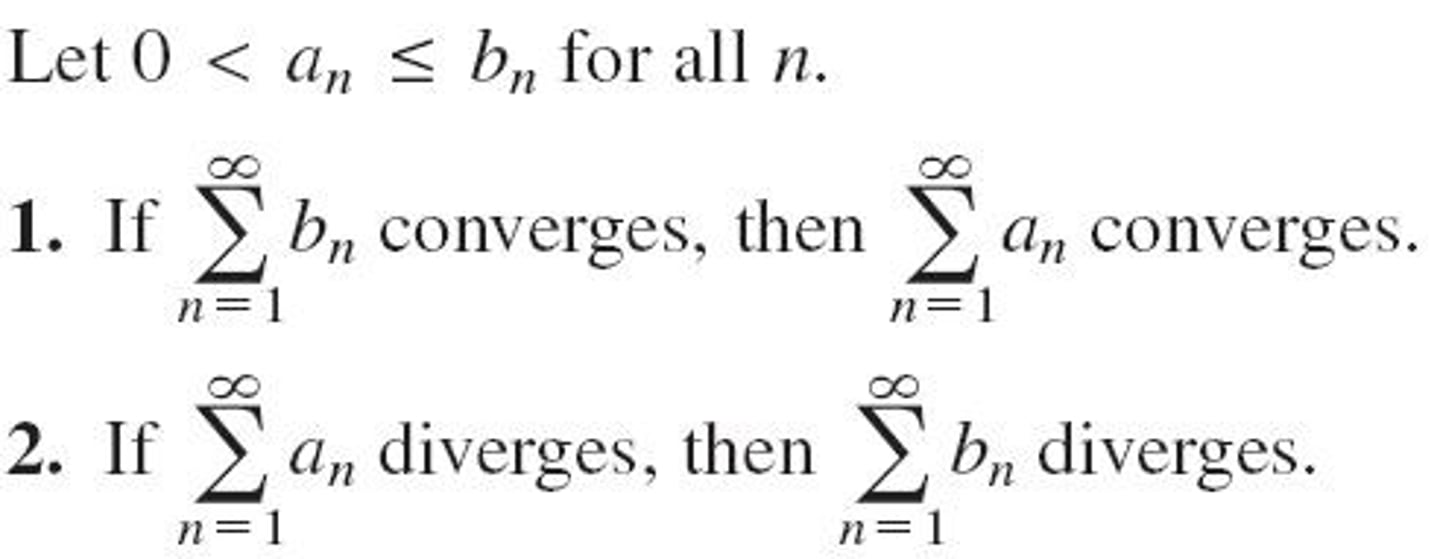
Limit Comparison Test

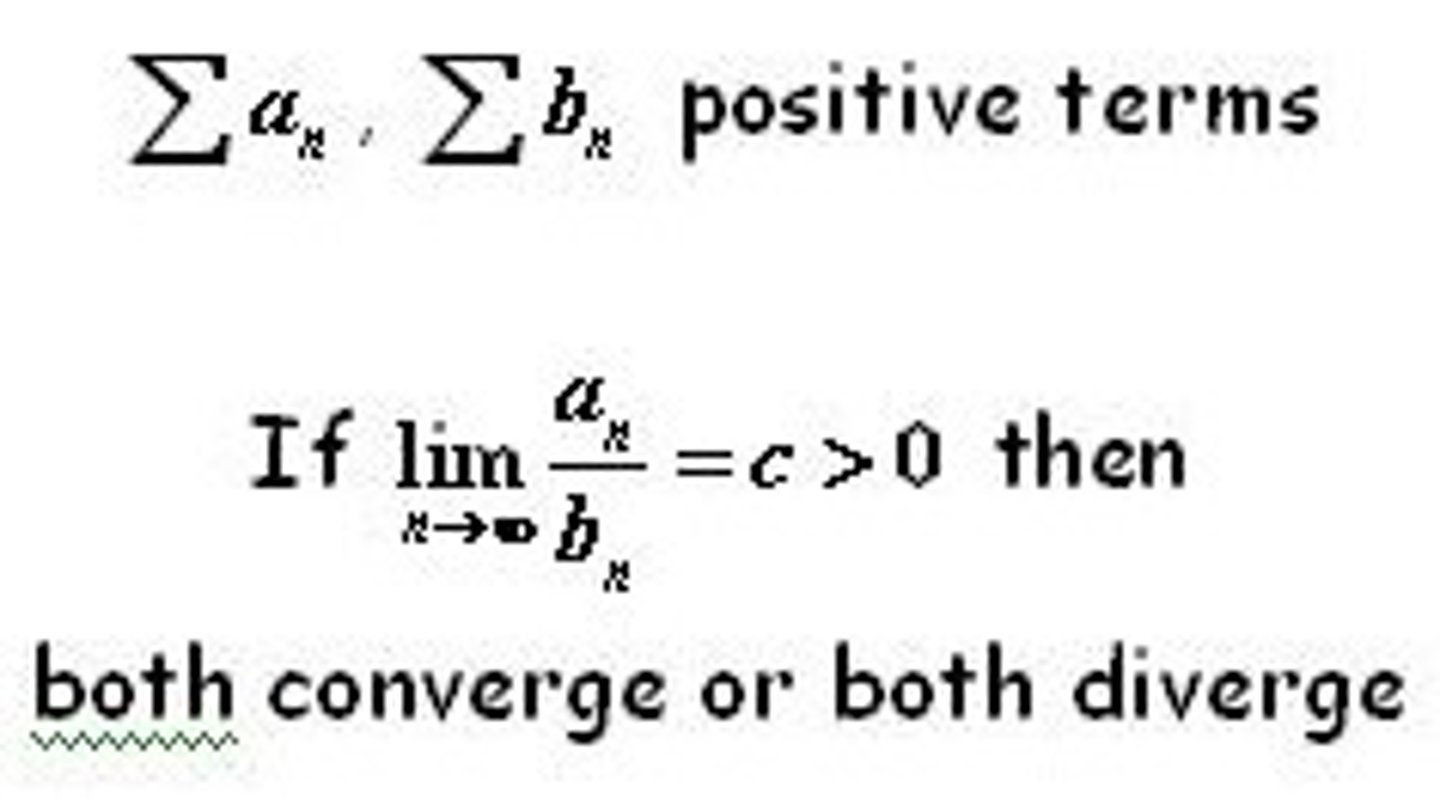
Ratio Test

lim n-> inf |(An+1 / An)| < 1 series converges

Interval of Convergence

Determined using ratio of convergence

Power Series

sum from n to infinity of (a*x^x)

Lagrange Error Bound