Capacitance 9702

9702 A Level Physics, 19 Capacitance

Capacitors

Electrical devices used to store energy.

Circuit symbol for parallel plate capacitor

Here

Capacitors store capacitance, which is defined as

The charge stored per unit potential.
(Or ratio of charge on an object to its potential)

Greater capacitance =

Greater charge stored on capacitor

2 forms capacitors come in

isolated spherical conductors, parallel plate capacitors

Isolated spherical conductors

- stores charge on its surface

- as p.d. of supply increases, the charge of the conductor also increases

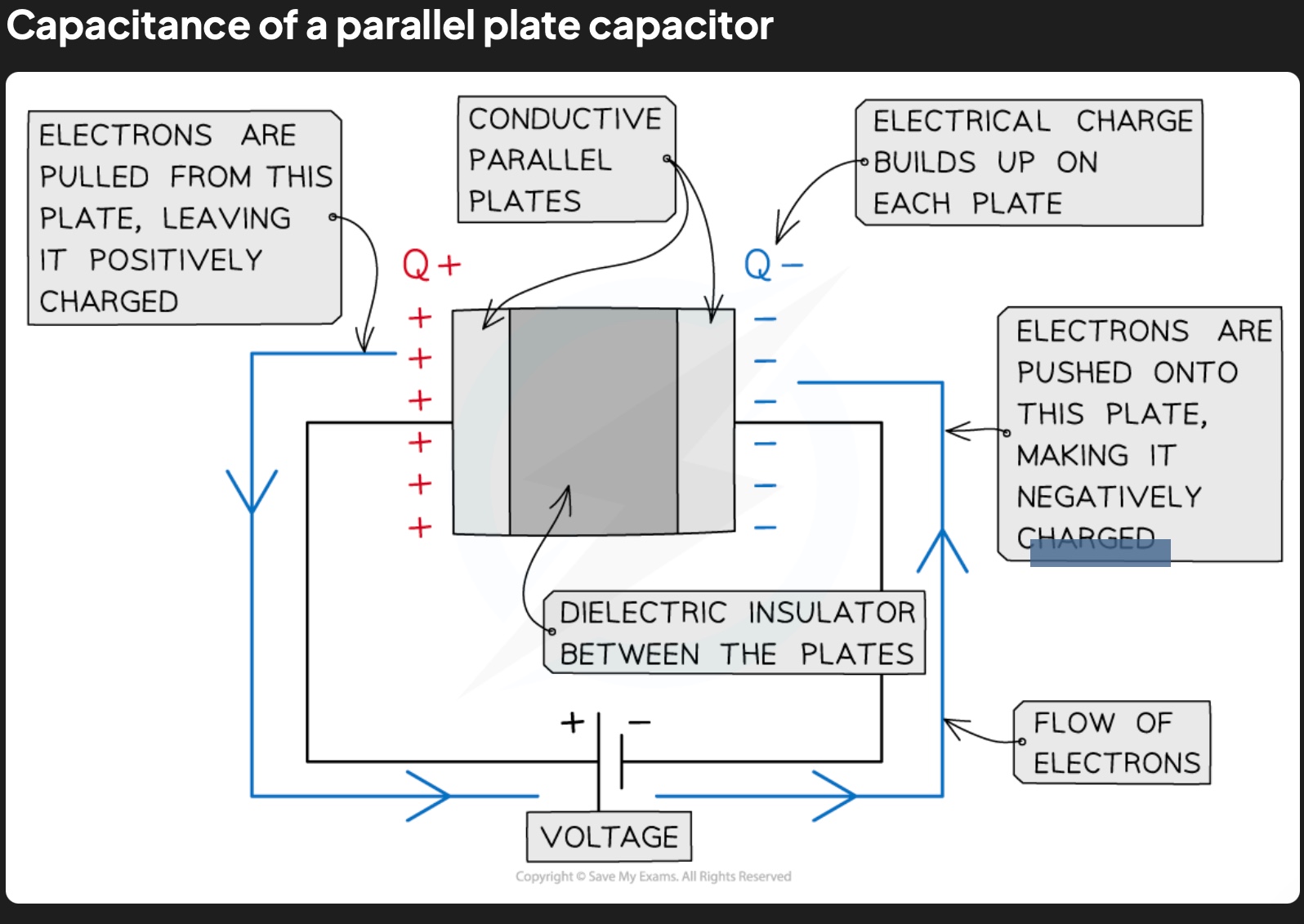
Parallel plates capacitors

- made up of two conducting metal plates connected to a voltage supply

- negative terminal of voltage supply pushes electrons onto one plate, making it negatively charged
- electrons repelled from opposite plate, making it positively charged
- there’s a (dielecteric) insulator between the plates which ensures charge doesn’t flow freely between the plates

charge stored by capacitor refers to

• magnitude of charge stored on each plate in a parallel plate capacitor/surface of a spherical conductor

• capacitor itself doesn’t store charge

capacitance formula

C = Q / V

• C = capacitance (F)

• Q = charge (C) … on plates

• V = potential difference (V) … across capacitor

unit of capacitance

• Farad (F) = 1 Coulomb per Volt, 1 C V^-1

capacitance of a spherical conductor

• charge per unit potential at surface of the sphere

  • because charge on surface of a spherical conductor can be considered as a point charge at its centre

  • Q= charge stored on surface of spherical conductor (not charge of capacitor)

• V of an isolated point charge =

  • V = Q/ (4πε₀R)

  • and C=Q/V so V=Q/C

  • so V=Q/C = V = Q/ (4πε₀R)

  • so C= 4πε₀R

combined capacitance of capacitors in a circuit depends on…

whether they’re connected in series or parallel

derive formulae for capacitance of capacitors in series

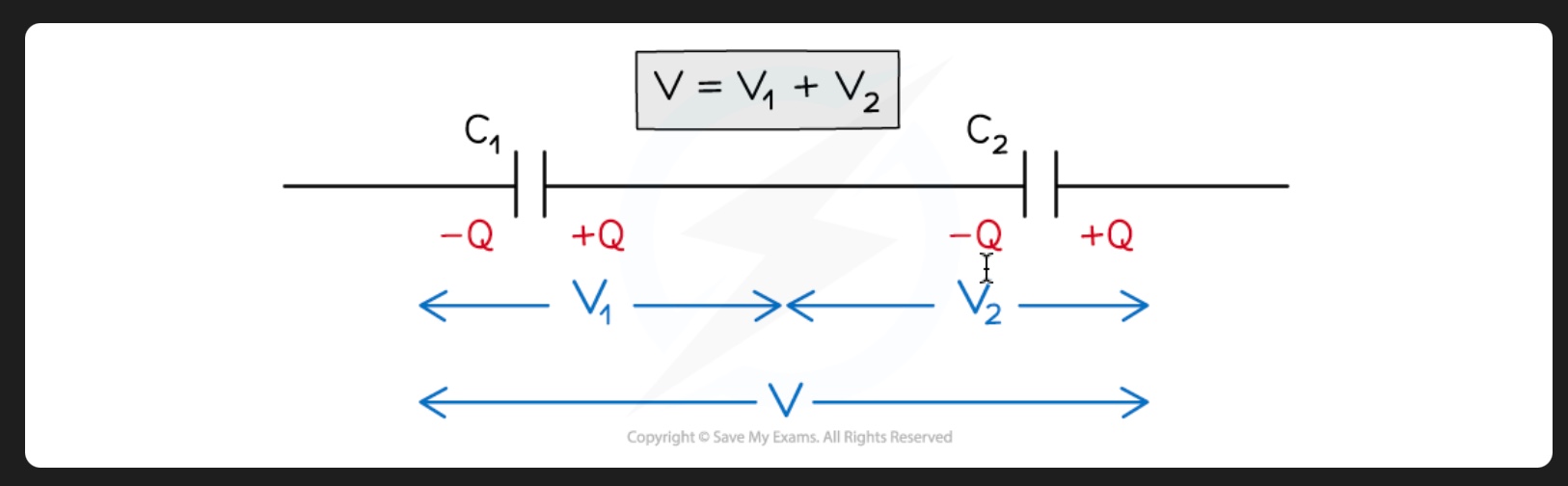
• consider 2 parallel plates capacitors C₁ and C₂ connected in series with a p.d. V across them

• in a series circuit, p.d. is shared between all the components in the circuit

  • therefore, if capacitors store same charge but diff. p.d.s, the p.d. across C₁ is V₁ and across C₂ is V₂

  • total p.d. V = sum of V₁ and V₂

  • V = V₁ + V₂

  • ∴ V₁ = Q/C₁ and V₂ = Q/C₂

  • total p.d. => V = Q/C_total

  • substitute into V = V₁ + V₂

    • Q/C_total = Q/C₁ + Q/C₂

• since current is same throughout all components in a series circuit, charge is same through each capacitor and cancels out

  • ∴ eqn. for combined capacitance in a series circuit

    • 1/C_total = 1/C₁ + 1/C₂ + 1/C₃ + …

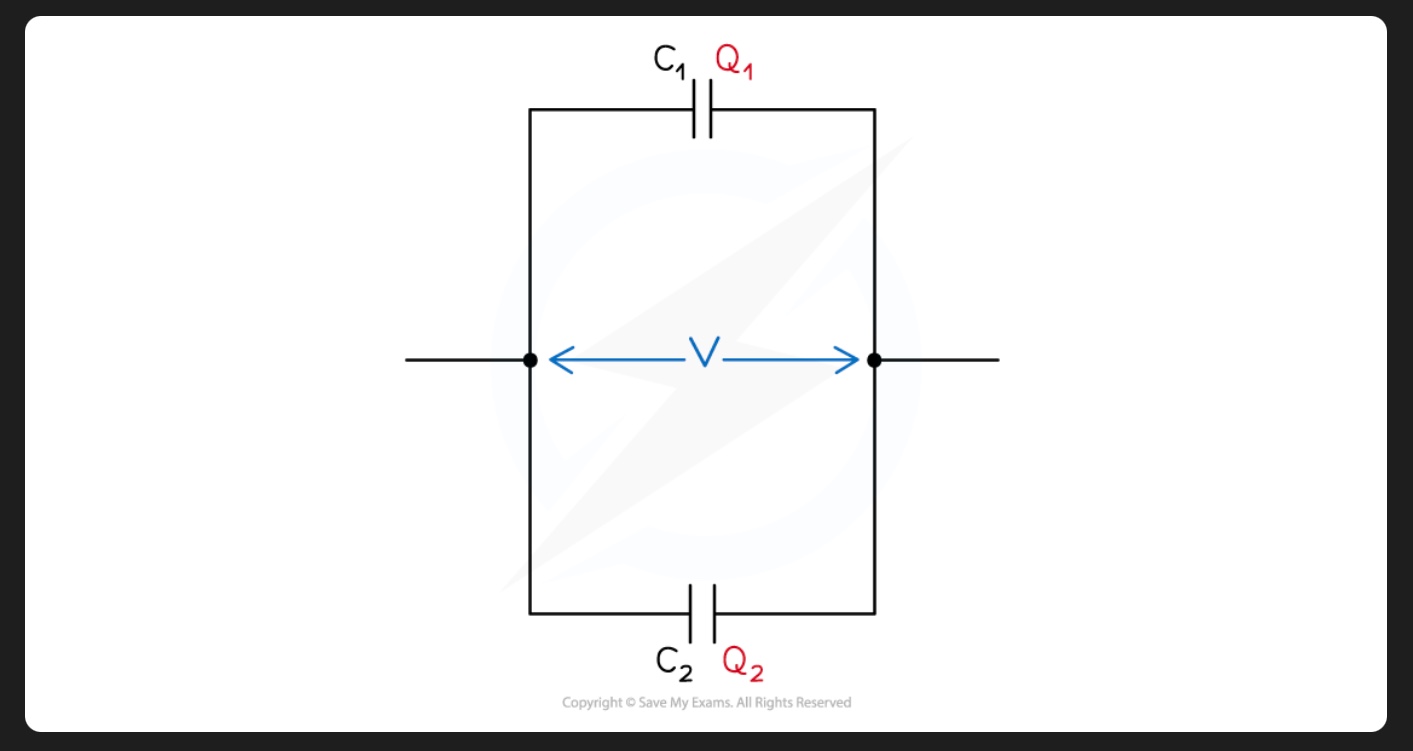
capacitors in parallel

• since current is split across each junction in a parallel circuit, the charge stored on each capacitor is different

  • therefore charge on capacitor C₁ is Q₁ and on C₂ is Q₂

• total charge Q:

  • Q_total = Q₁ + Q₂

• therefore (by rearranging capacitance eqn.)

  • Q₁=C₁V and Q₂=C₂V

• total charge Q is defined by total capacitance

  • Q_total = C_totalV

• substitute in Q_total = Q₁ + Q₂

  • C_totalV = C₁V + C₂V

• since p.d. is same across all components in a parallel circuit, p.d. V cancels out

  • ∴ combined capacitance of capacitors in parallel

  • C_total = C₁ + C₂ + C₃ +…

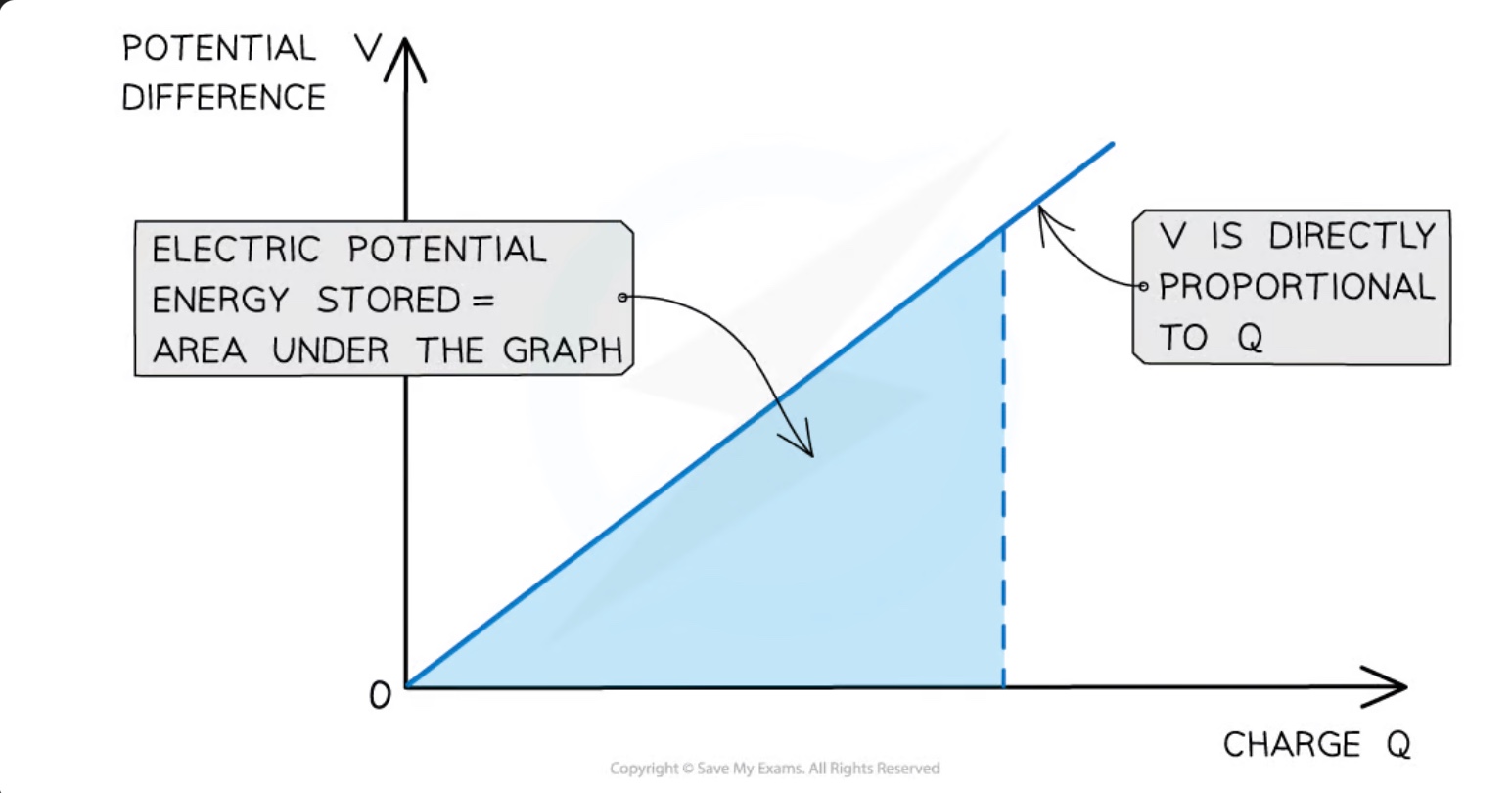
determine the electrical potential energy stored in a capacitor from a potential charge-graph

• electrical potential energy stored in a capacitor = area under potential-charge graph

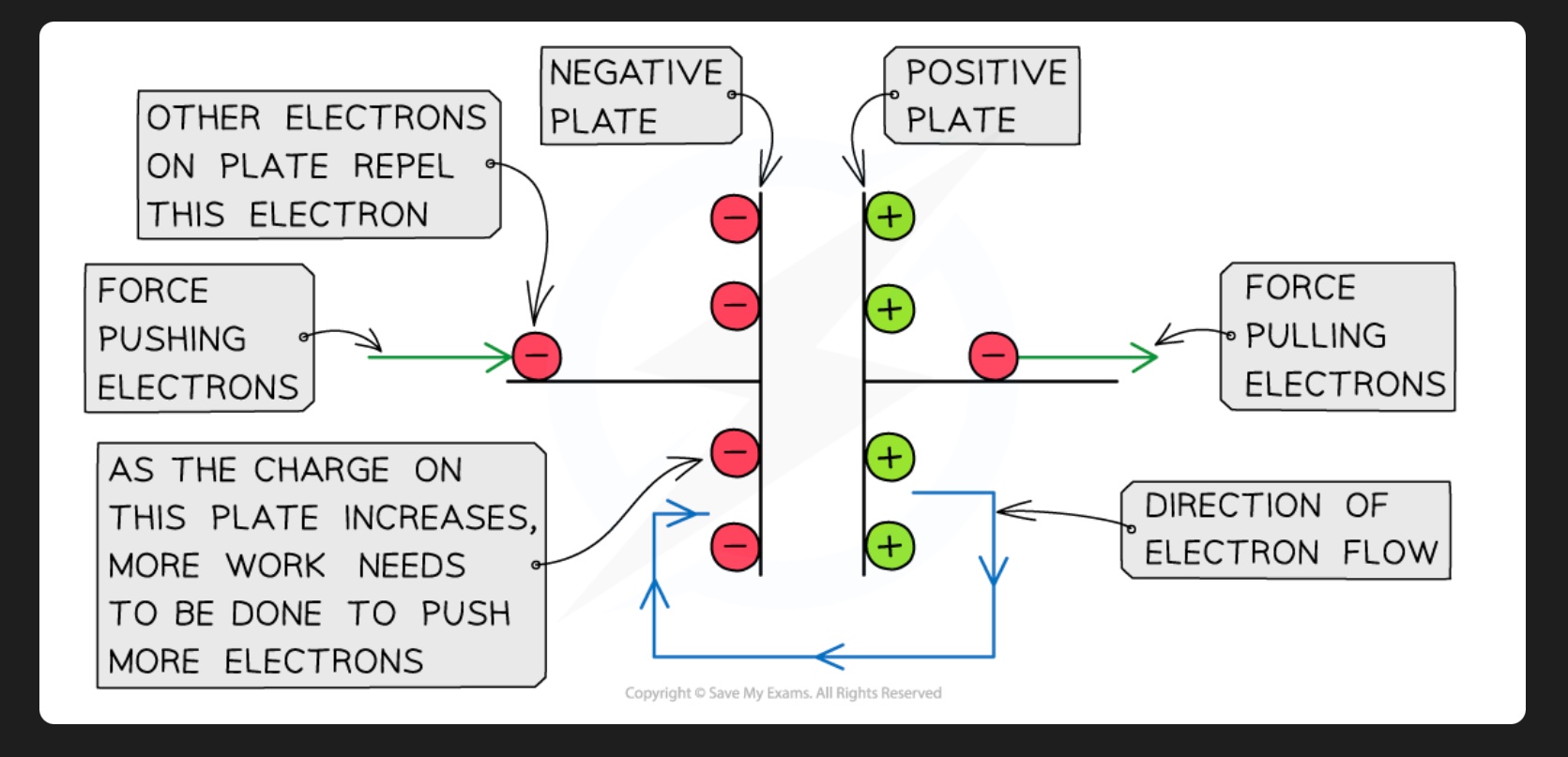
how electrical potential energy is produced on a capacitor

• when charging a capacitor, power supply transfers electrons on one plate, giving it a negative charge, and transfers electrons away from the other plate, giving it a positive charge

  • ∴ it does work on the electrons, which increases their electrical potential energy

• as charge of negative plate increases, the electric repulsion between electrons increases

  • thus greater amount of work needs to be done to increase the charge on the negative plate

• also, charge Q on the capacitor is directly proportional to its p.d. V, so the graph is a straight line passing through the origin

energy stored in a capacitor formula

• electrical potential energy is equal to the area under a potential-charge graph

  • this is equal to the work done in charging the capacitor across a particular p.d.

• ∴ the work done/energy stored in a capacitor is defined by

  • W = ½ QV

• substitute charge as C = Q/V ∴ Q=VC

  • ∴ W = ½ CV²

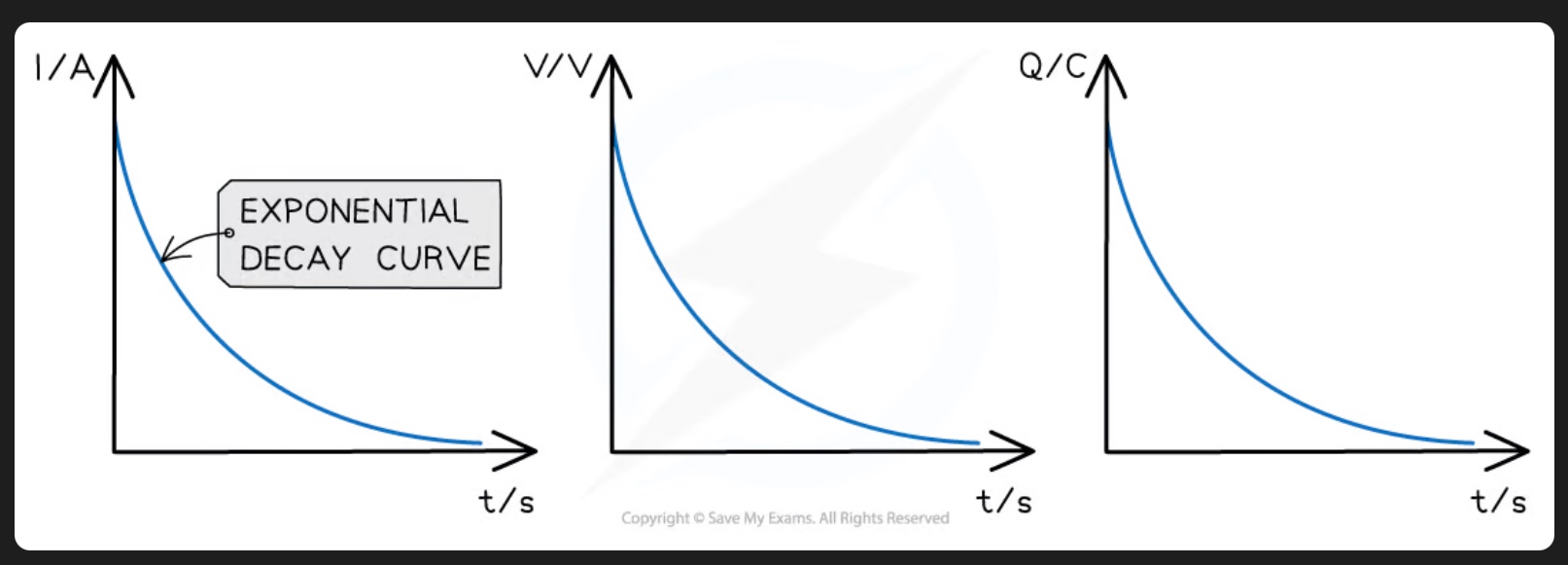
capacitor discharge graphs

• capacitors are discharged through a resistor

  • electrons flow from negative plate to positive plate until there are equal numbers on each plate

• as capacitor discharges, the current, p.d. and charge all decrease exponentially

  • so these graphs w.r.t. to time are all identical and represent exponential decay

the rate at which a capacitor discharges depends upon…

• the resistance of the circuit

  • high resistance = current decreases = charge flows from capacitor plates more slowly = more time for capacitor to discharge

  • & vice versa

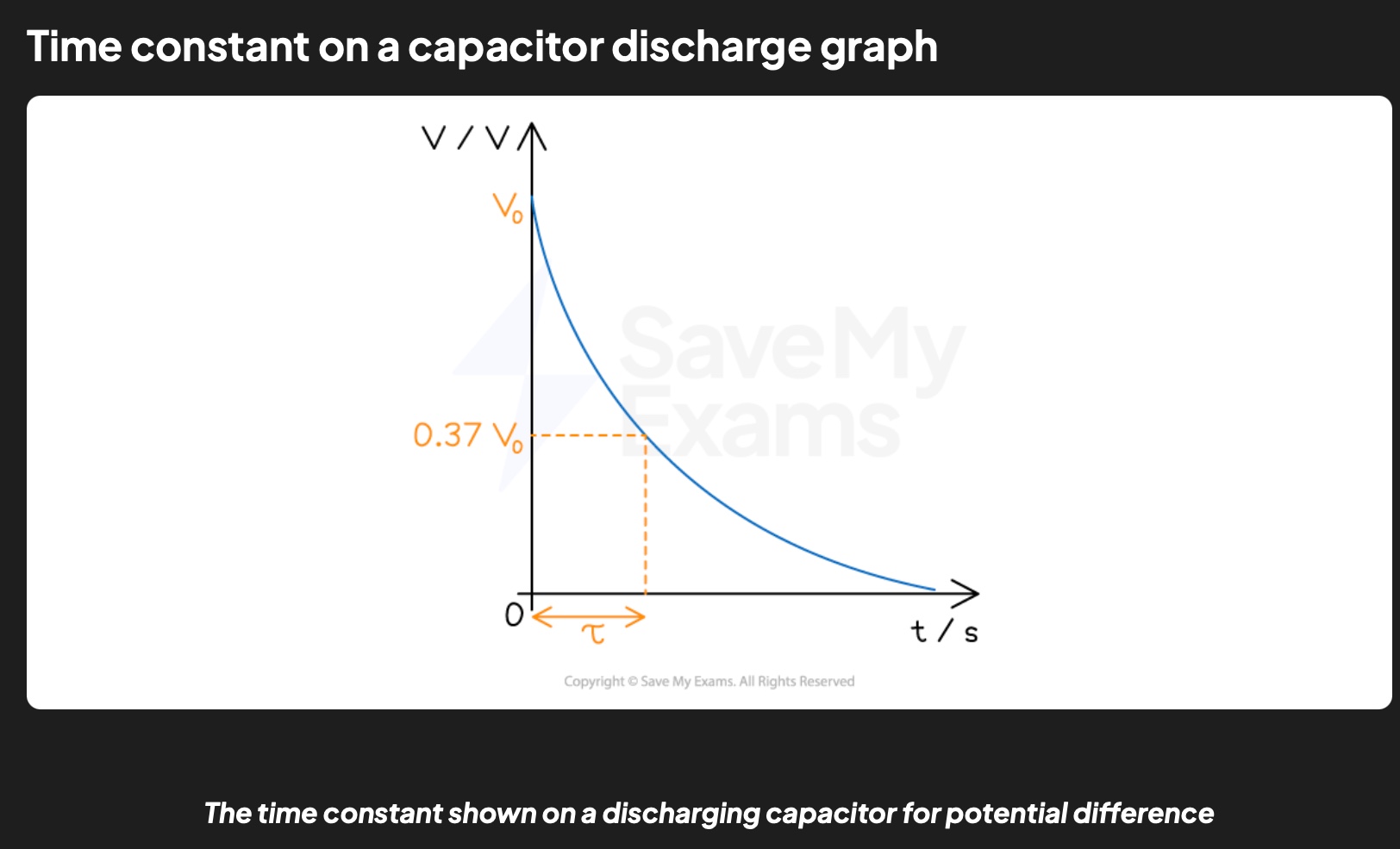
time constant, (𝜏), of a capacitor discharging through a resistor

• a measure of how long it takes for the capacitor to discharge

• defined as: the time taken for the charge, current or voltage of a discharging capacitor to decrease to 37% of its original value

• unit seconds

time constant 𝜏 equation

• 𝜏 = RC

• 𝜏 = time constant (s)

• R = resistance of resistor (Ω)

• C = capacitance of capacitor (F)

find time constant from graph

• find 0.37V₀ and the corresponding time for that value = time constant

capacitor discharge equation

• x = x₀e^-(t/RC)

• x = current, charge or p.d.

• x₀ = initial current, charge or p.d. before discharge

• e = the exponential function

• t = current time/time elapsed

• RC = resistance (Ω) * capacitance (C) = time constant (𝜏)

equation shows that greater time constant… and greater initial current…

• greater time constant = greater the speed at which current/charge/p.d. falls during discharge

• greater initial current/charge/p.d. = greater rate of discharge (capacitor will take longer to discharge)