AP Calculus BC

Units 1-9 currently

a limit must be a ___ and ____ value

fixed, finite

ways a limit doesn’t exist

left handed limit doesn’t equal right handed limit

f(x) has asymptote as x approaches c

f(x) oscillates between 2 fixed values as x approaches c

f(x) doesn’t exist around the place where x is approaching c

1

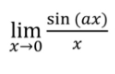
a

limit properties

if the limit properties don’t apply (because one of the limits doesn’t exist) then

you can split the whole limit into left handed and right handed limits

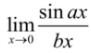
a/b

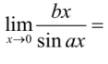
b/a

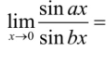
a/b

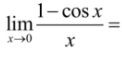
0

limit of a composite function

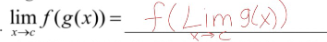
the limit of a composite function theorem only works if f(x) is

defined and continuous at lim (g(x)) as x approaches c

squeeze theorem

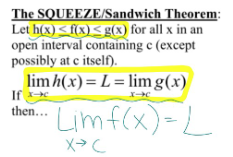
continuity at a point

continuity over an open interval

function is continuous at every point in the interval

continuity over a closed interval

non removeable discontinuities

Vertical asymptotes and jumps

removeable discontinuities

holes

properties of continuity

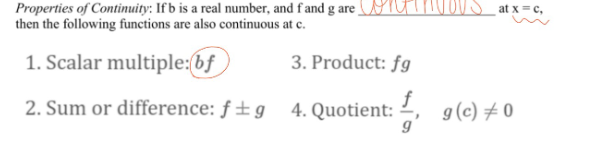
f(x) approaches positive or negative infinity as x approaches c from the right or the left, then the line x=c is a

vertical asymptote

limit at infinity of a polynomial and greatest degree bigger on bottom

HA: y=0

limit at infinity of a polynomial and greatest degree bigger on top

no HA

limit at infinity of a polynomial and degree on top and bottom are same

HA: y=divide coefficients

relative magnitudes of functions

Ten fabulous engineers prefer learning calculus

Tower

Factorials

Exponentials

Polynomials

Logarithms

Constants

intermediate value theorem

state continuity on the closed interval. if k is any number between f(a) and f(b) then there is at least one number in the closed interval such a that f(c)=k

what must be stated for IVT

continuity on closed interval, and the value lies between the given endpoints of the interval

therefore statement for IVT

therefore IVT guarantees some x=c on [a,b] such that f(c)=number

AROC

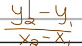
difference quotient

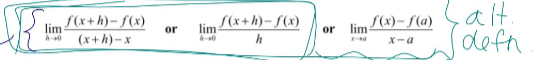
derivative

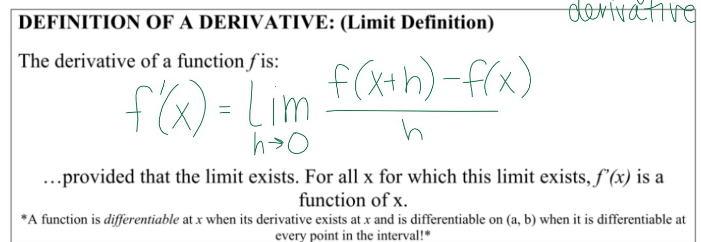
derivative notation

alternate definition of a derivative

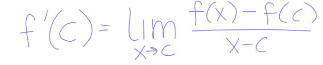
derivatives do not exist at

endpoint of domain or closed interval

corners and cusps

jumps

vertical asymptotes

differentiability implies

continuity

power rule for differentiation

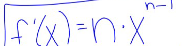
sum and difference rule (differentiating)

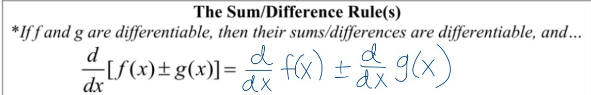
constant multiple rule (differentiating)

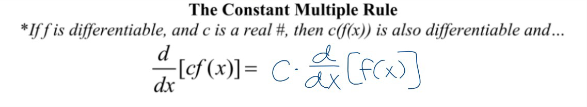
derivative of sinx

cosxd

derivative of cosx

-sinx

derivative of e^x

e^x

derivative of lnx

1/x

derivative of tanx

sec²x

derivative of cotx

-csc²x

derivative of secx

secxtanx

derivative of cscx

-cscxcotx

product rule

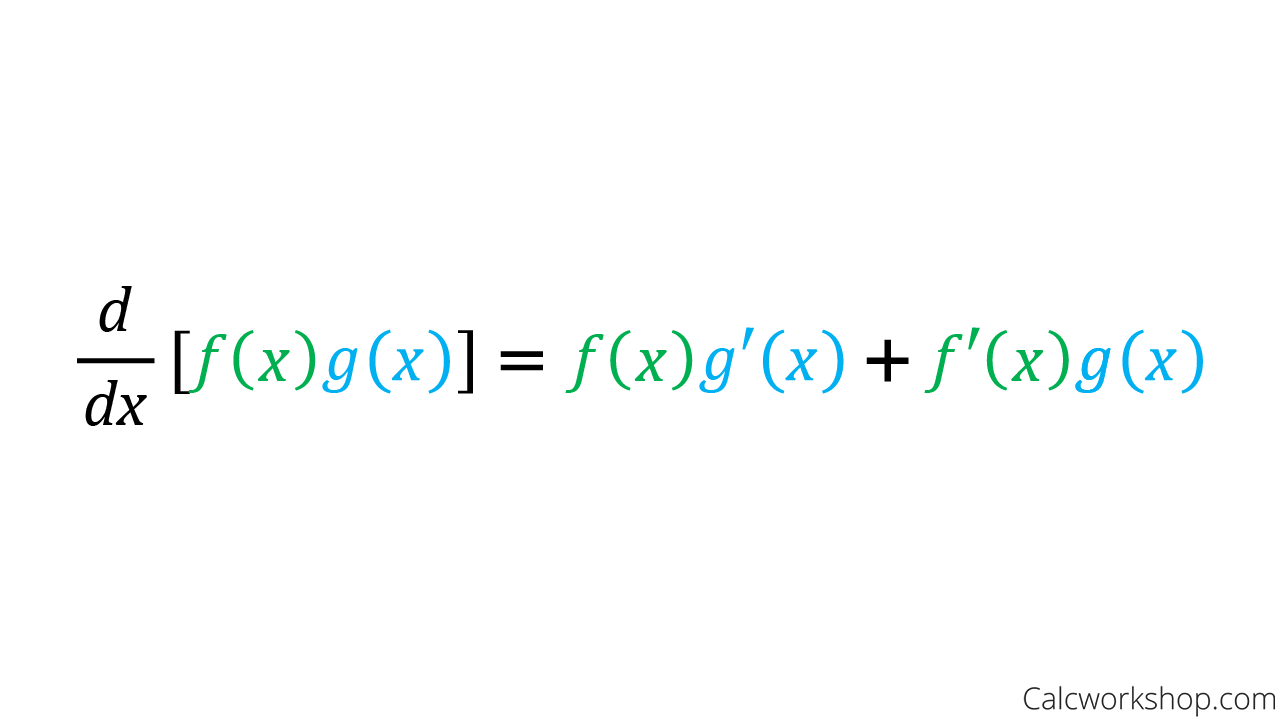
quotient rule

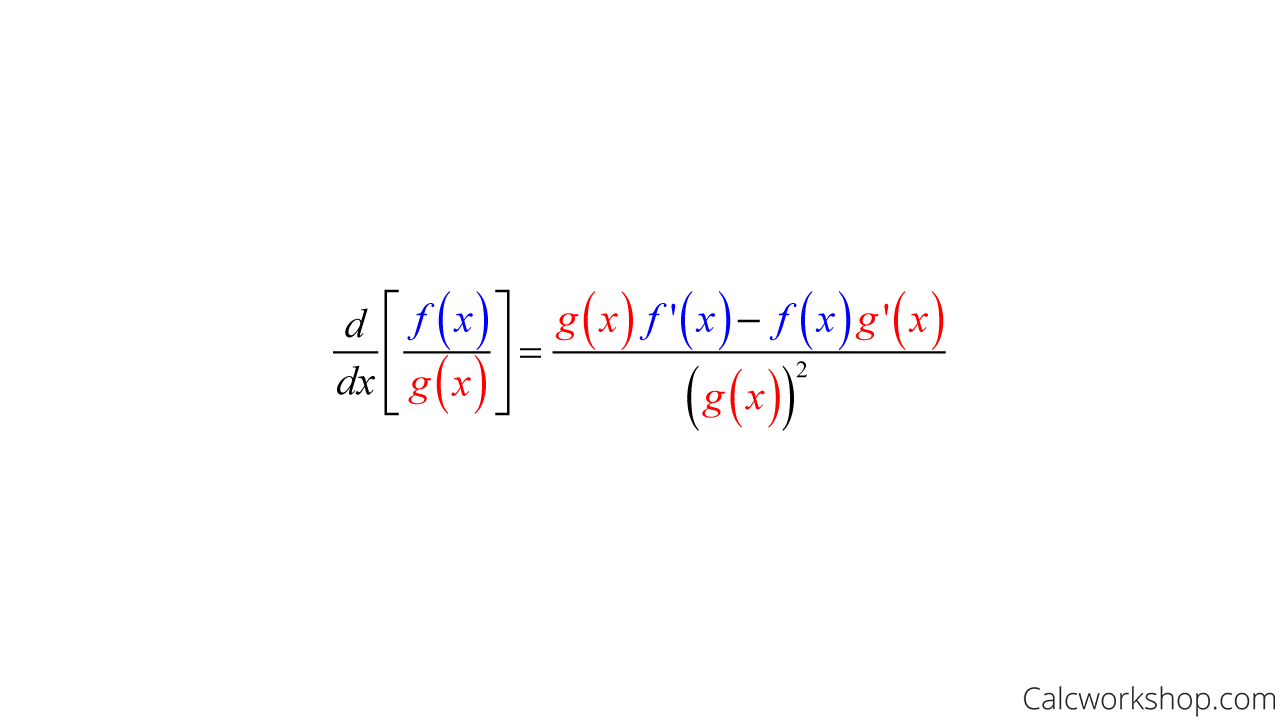
chain rule lets us take the derivative of a

composite function

chain rule

general power rule for differentiation (with chain rule)

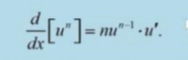
derivative of ln(u)

u’/u

derivative of ln|u|

u’/u (no change because of absolute value)

logarithmic differentiation

take the natural log of both sides and then differentiate

why is implicit differentiation necessary

some equations cannot be expressed explicitly with y as a function of x

when implicitly differentiating we must apply

chain rule

continuity and differentiability of inverse functions

derivative of an inverse function

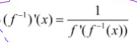
inverse functions have _____ slopes at ____ points

reciprocal, corresponding

restrictions for inverse trig functions: Q1+Q4

sin^-1(x), csc^-1(x), tan^-1(x)

restrictions for inverse trig functions: Q1+Q2

cos^-1(x), sec^-1(x), cot^-1(x)

derivatives of inverse trig functions

notation of higher order derivatives

higher order implicit differentiation

interpreting a derivative

the f(t) is (increasing/decreasing) at a rate of f’(t) + units at t= time with units

related rates

use chain rule

local linearity

if zoomed in close enough, any function will start to look linear

when will linear approximation overestimate versus underestimate

concave up: under approximate

concave down: over approximate

L’Hospital’s Rule

if the numerator and the denominator of a limit are both 0 or are both + or - infinity, then the limit of the derivative of the numerator divided by the derivative of the denominator is the answer

Rolle’s Theorem

state continuity on closed interval, differentiability on the open interval, state that endpoint values are equivalent f(a)=f(b). Rolles guarantees some x=c on the open interval such that f’(c)=0.

Mean Value Theorem

state continuity on the closed interval and differentiability on the open interval. MVT guarantees some x=c on the open interval such a that f’(c)=avg rate of change

Extreme Value Theorem

state continuity on the closed interval. f(x) has both a minimum and a maximum on that interval.

critical number/value

f’(c)=0 or if f is not differentiable at c. only time f(x) can change direction

f’(x)>0

f(x) is increasing

f’(x)<0

f(x) is decreasing

f’(x)=0

possible max/min

f(x) goes from increasing to decreasing

relative max

f(x) goes from decreasing to increasing

relative min

first derivative test

take first derivative, find critical values, result is minimum or maximum values

candidates test

the only points eligible to be absolute extrema are critical points and endpoints of a closed interval. find the x values of each and the corresponding f(x) values

f’’(x) > 0

f(x) is concave up

f’’(x) < 0

f(x) is concave down

points of inflection

f’’(x)=0 or f’’(x) is undefined

second derivative test

find critical values, evaluate second derivative at the critical values. if f’’(c)>0 then there is relative min, if f’’(c)<0 there is a relative max. if f’’(c)=0 the test fails and use the first derivative test

optimization

create optimized and constraint equations. substitute the constraint into the optimized equation. take first derivative and set equal to zero

when does an implicit equation have critical values

when dy/dx = 0 or is undefined

when does an implicit equation have horizontal tangent lines

when the numerator of dy/dx is 0

when does an implicit equation have vertical tangent lines

when the denominator of dy/dx is zero

accumulated area under the x axis is considered to be

negative

3 different kinds of Riemann sums

left handed, right handed, midpoint

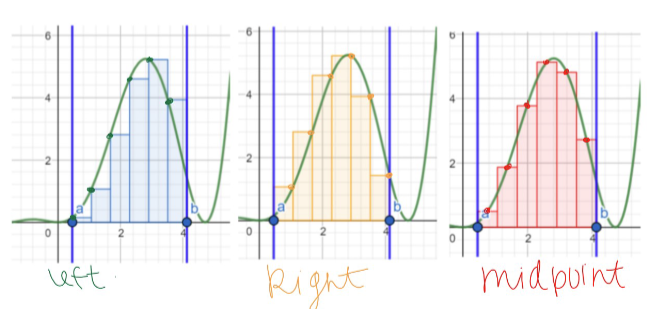
when do Riemann sums give over approximations

left handed: curve is decreasing

right handed: curve is increasing

midpoint: curve is concave down

when do Riemann sums give under approximations

left handed: curve is increasing

right handed: curve is decreasing

midpoint: curve is concave up

identify the parts of a definite integral

how do you read an integral

the integral from a to b of f(x) with respect to x

continuity implies

integrability

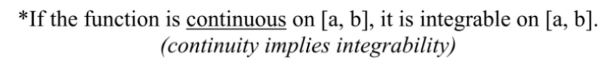
an integral might not represent the area under the curve if part of the curve is

negative (under x axis)

differentiation and integration are ____ operations

inverse

first fundamental theorem of calculus (part 1)

if f is a continuous function on an interval containing a, then the derivative of the accumulation from a to x of f(t) dt is equal to f(x)

integral of the sum of functions property for integrals

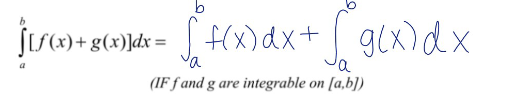
adjacent intervals property for definite integrals

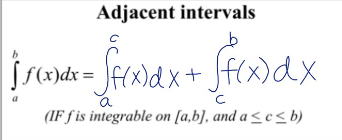
if a definite integral has the same upper and lower bound the integral is equal to

zero