5.2 circular motion

radians

you already know this no need to do it again

period

T, seconds taken for an object to travel a full circle

frequency

f, (measured in Hertz) the number of full circles completed in one second

f = 1/T

angular velocity

ω the rate of change of angle of an object moving in a circle
ω = θ/t and is measured in rad/s

centripetal force

the net force which acts towards the centre of the circle during circular motion (parallel to the direction velocity of the orbital object), causing a change in acceleration necessary for the continuation of orbital motion
f = (mv^2)/r = mωr^2
where F = force(N), m = mass(kg), v = velocity(m/s), r = radius(m), ω = angular velocity

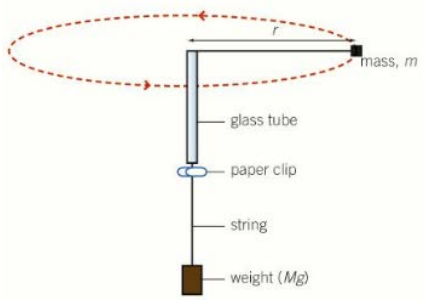
techniques to investigate circular motion pt.1

-tie a bung with a known mass to a piece of string and thread it through a glass tube
-suspend a known mass from the other end of the string
-whirl the string in a circle and record the time taken for a complete rotation
-alter the mass and repeat the experiment
-as the centripetal force in this experiment is provided by the tension in the string, their equations can be equated i.e.
(mv^2)/r = Mg

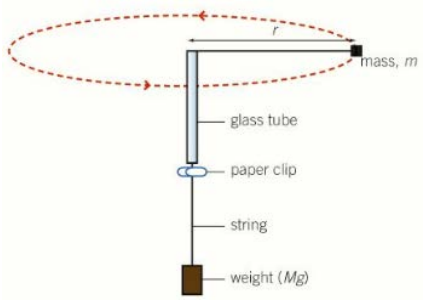
techniques to investigate circular motion pt.2

(mv^2)/r = Mg
where m is the mass of the object subjected to circular motion (the bung)
v is the speed of the circular motion
r is the length of string forming the radius of the circle (from the bung to the top of the glass tube)
M is the mass of the weight that provides the tension in the string, providing the centripetal force
and g is gravity