Electronic Structure of Atoms

electronic structure

number of electrons in the atom, their distribution around the nucleus, and their energies

electromagnetic radiation (radiant energy)

form of energy that has wave characteristics

wavelength (λ)

distance between two peaks or troughs

m, meters

frequency (ν)

number of complete wavelengths that pass through a certain point

must be in Hz, s^-1

speed of light (c)

= 3.00 x 10⁸ m/s

quantity at which all types of electromagnetic energy moves

equation for electromagnetic radiation

c = λν

(c = 3.00 x 10⁸ m/s, ν = frequency in s⁻¹, λ = wavelength in m)

what did Maxwell Planck suggest about energy

energy could be emitted or absorbed in increments/levels

quantum

refers to the smallest quantity of energy that can be emitted or absorbed as electromagnetic radiation

equation for quantum energy

E = hν

(E = energy of single quantum, h = 6.626 x 10⁻³⁴ J-s, ν = frequency)

what does h stand for

Planck's constant, 6.626 x 10⁻³⁴ J-s

be able to recognize, don't need to memorize

how does hv relate to matter

matter can emit or absorb energy in whole number multiples of hv

photoelectric effect

metals emit electrons when light is shined on them

what is required for photoelectric effect to occur

minimum frequency of light is required and is different for each metal

photon

energy packet of light

equations for photon energy

E = hv

E = hc/λ

what do photons do

photons transfer energy to the electrons; if photons have enough energy, the electrons can escape from the metal

summary of light equations

electromagnetic radiation: c = λν

quantum energy: E = hν

photon energy: E = hv, E = hc/λ

spectrum

made when radiation from polychromatic light source is split into its component wavelengths with a prism

continuous spectrum

contains almost all wavelengths/colors (ex. rainbows)

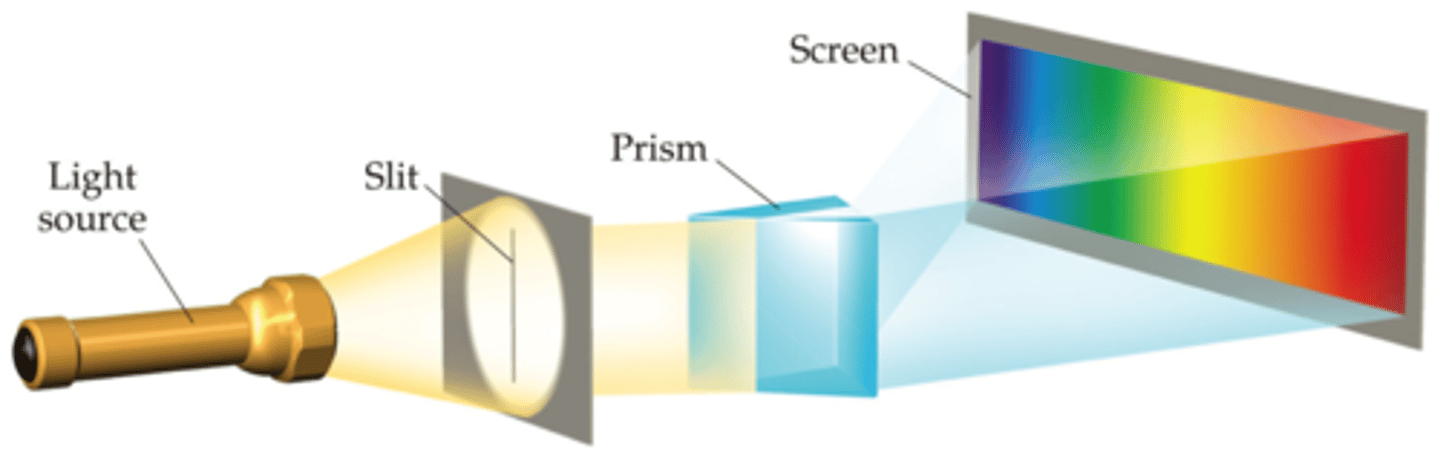
line spectra

contain only a few specific wavelengths/colors (ex. when voltage is applied to a gas under low pressure, neon lights)

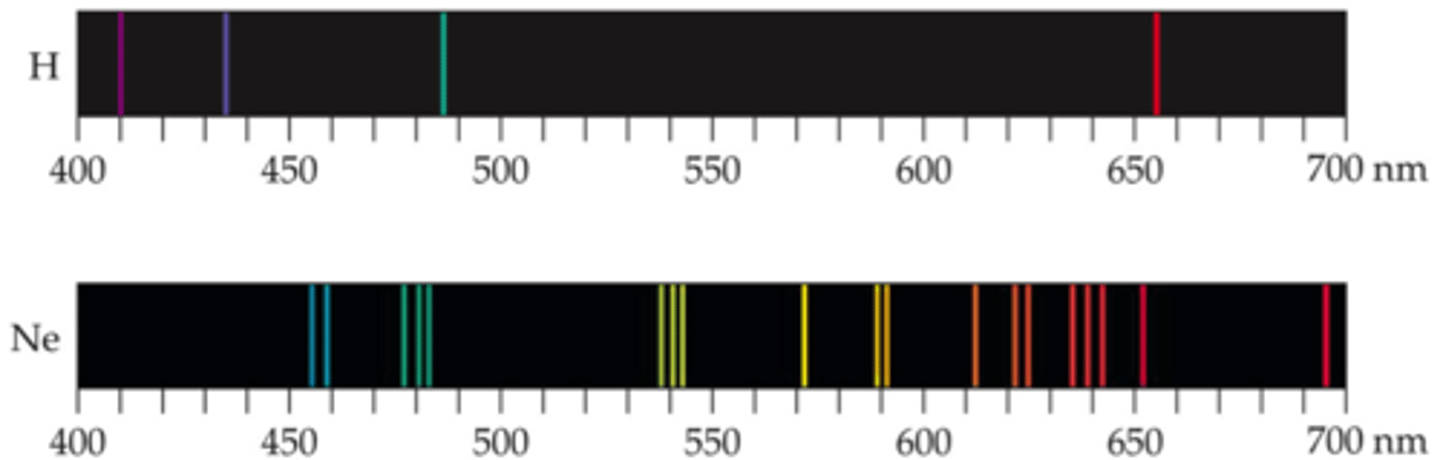
Postulates for H atom (Bohr Model of the Atom)

1. Only orbits of certain radii, corresponding to specific energies, are permitted for the electron is a H atom.

2. An electron in a permitted orbit is in an "allowed" energy state. In this state, it does not radiate energy and does not spiral into nucleus.

3. Energy is emitted or absorbed by the electron only as the electron changes from one allowed energy state to another. This energy is emitted or absorbed as a photon that has energy E = hν.

equation for energies corresponding to the allowed orbits for the electron in H atom

E = (-2.18x10⁻¹⁸ J)(1/n²) = (-hcRH)(1/n²)

n = principal quantum number (whole number)

principle quantum number

each allowed orbit corresponds to different value of n

radius increases as n increases

ground state

closest state to the nucleus (n = 1)

lowest energy and therefore the most stable (most energy)

excited states

everything that isn't ground state (n = 2+)

higher energy, less stable states

reference or zero energy state

when electron is separated from the nucleus (n = infinity)

what do electrons do when they change energy states

electrons will absorb or emit radiant energy

equation for change in energy

ΔE = Ef - Ei

ΔE = (-2.18x10-18 J)(1/nf2 - 1/ni2)

+ΔE = e- absorb energy to move to a higher state/n.

-ΔE = e- emit energy to move to a lower state/n.

how is energy absorbed or emitted as

photons

+ΔE (nf > ni);

ΔE = hν = Ephoton

photon absorbed

-ΔE (nf < ni);

- ΔE = hν = Ephoton

photon emitted

what tells you whether the photon is absorbed or emitted since h and v are positive

the sign

the lines in a line spectra can be attributed to

quantized jumps of electrons between energy levels

limitations of Bohr model

only fully explains a hydrogen atom

assumes that electron wouldn't fall into nucleus

electron has wave-like properties; doesn't just "circle" the nucleus

significance of Bohr's model

electrons only exist in discrete energy levels, which are described by quantum numbers

energy is involved in the transition of an electron from one energy state to another

what did Louis de Broglie suggest that electrons could behave like

a wave, more specifically matter waves

matter waves equation

λ = h / (mv)

m = mass in kg

v = velocity in m/s

mv = momentum

Heisenberg's uncertainty principle

states that it is impossible for us to know simultaneously both the exact momentum and exact position of particles with a small mass (i.e. electrons).

ncertainty of position: Δx ≥ h/(4πmΔv)

x = position

quantum mechanics

an approach to electronic structure that incorporates both wave-like and particle-like behaviors of the electron

Schrodinger proposed a

wave equation and wave functions (ψ) that treat electrons as standing waves that haves nodes or points where the magnitude of the wave is 0.

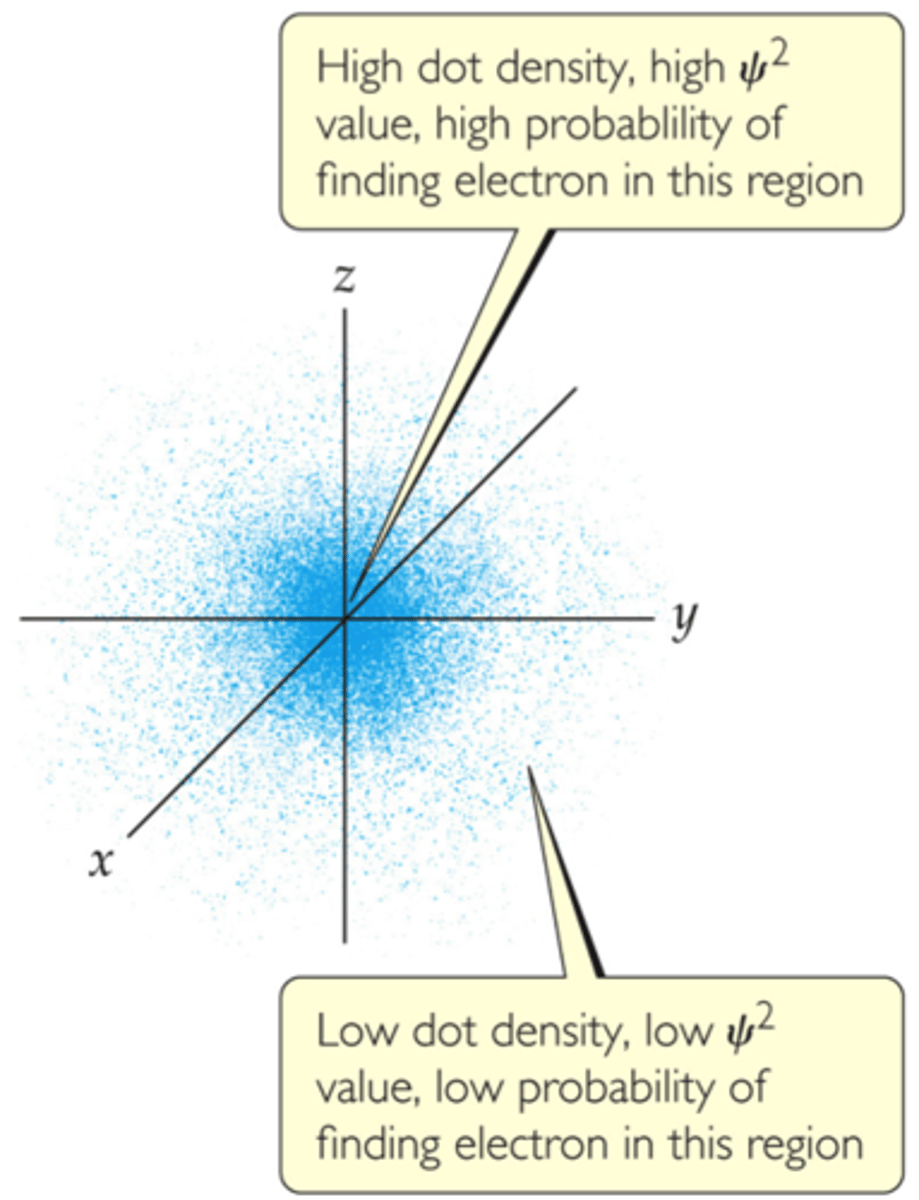
probability or electron density (ψ2)

represents the probability that an electron will be found at some location

orbitals

regions within an atom where electrons are most likely to be found

quantum numbers are

used to describe the characteristic shape and energy of each orbital

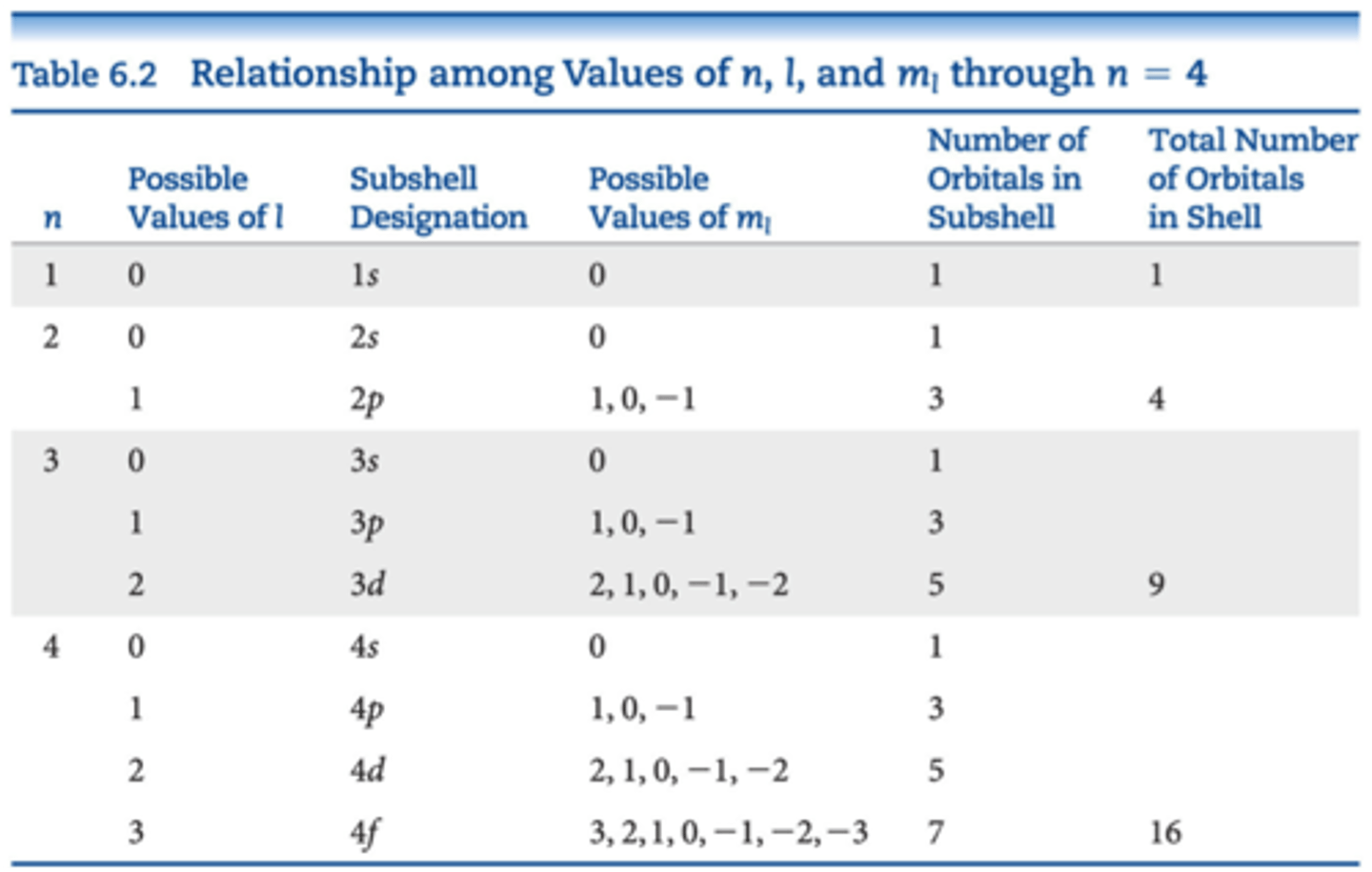
n, l, ml, s

n

principal quantum number

same principles from Boh's model apply

En = -2.18 x 10^-18 J (1/n^2)

l

angular momentum quantum number

values range from 0 to (n-1) for each n

defines the shape of the orbital

usually designated by letters

ml

magnetic quantum number

values are whole numbers between -l and l including 0.

describes the orientation of the orbital

ms

spin number

describes the spin

1/2 or -1/2

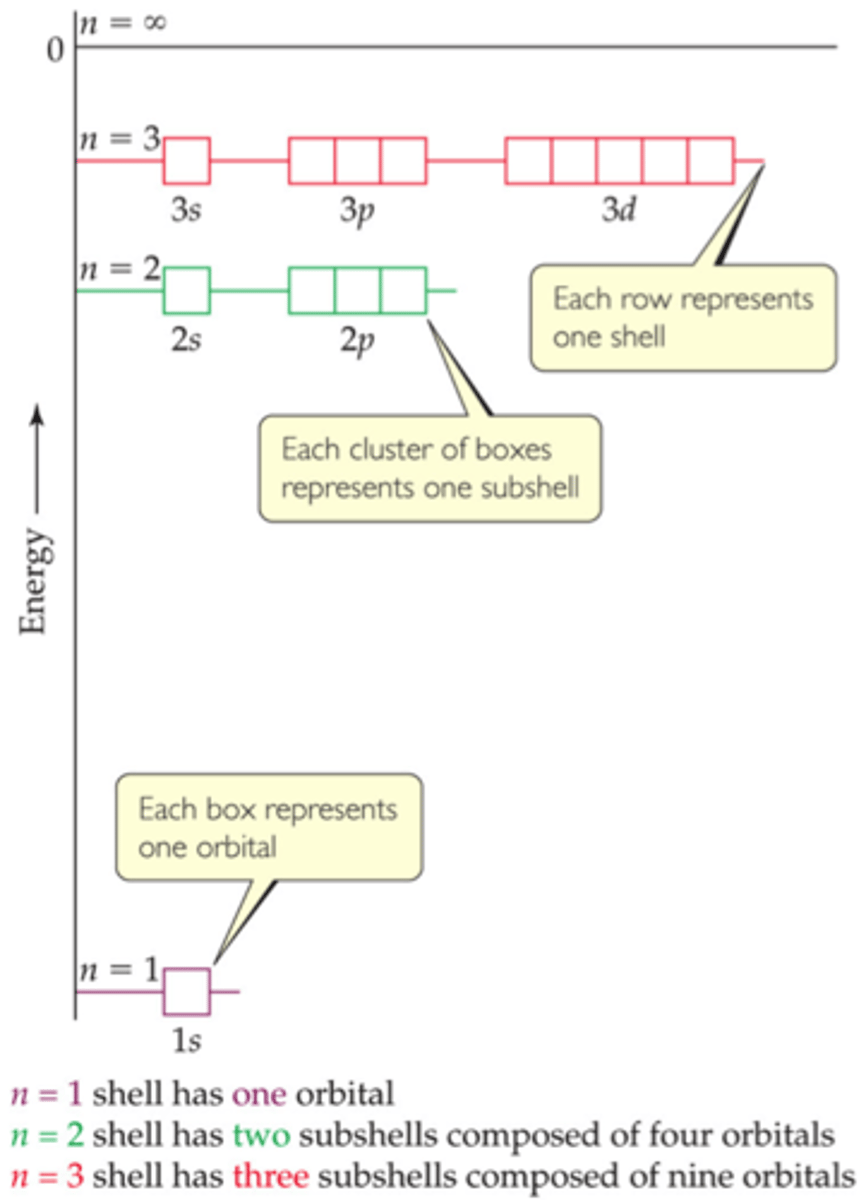
electron shells

collections of orbitals with the same n

subshells

have same n and l values

designated by a number and a letter

a shell only contains n number of subshells

each subshell consists of a specific number of orbitals

the total number of orbitals in a shell is n^2

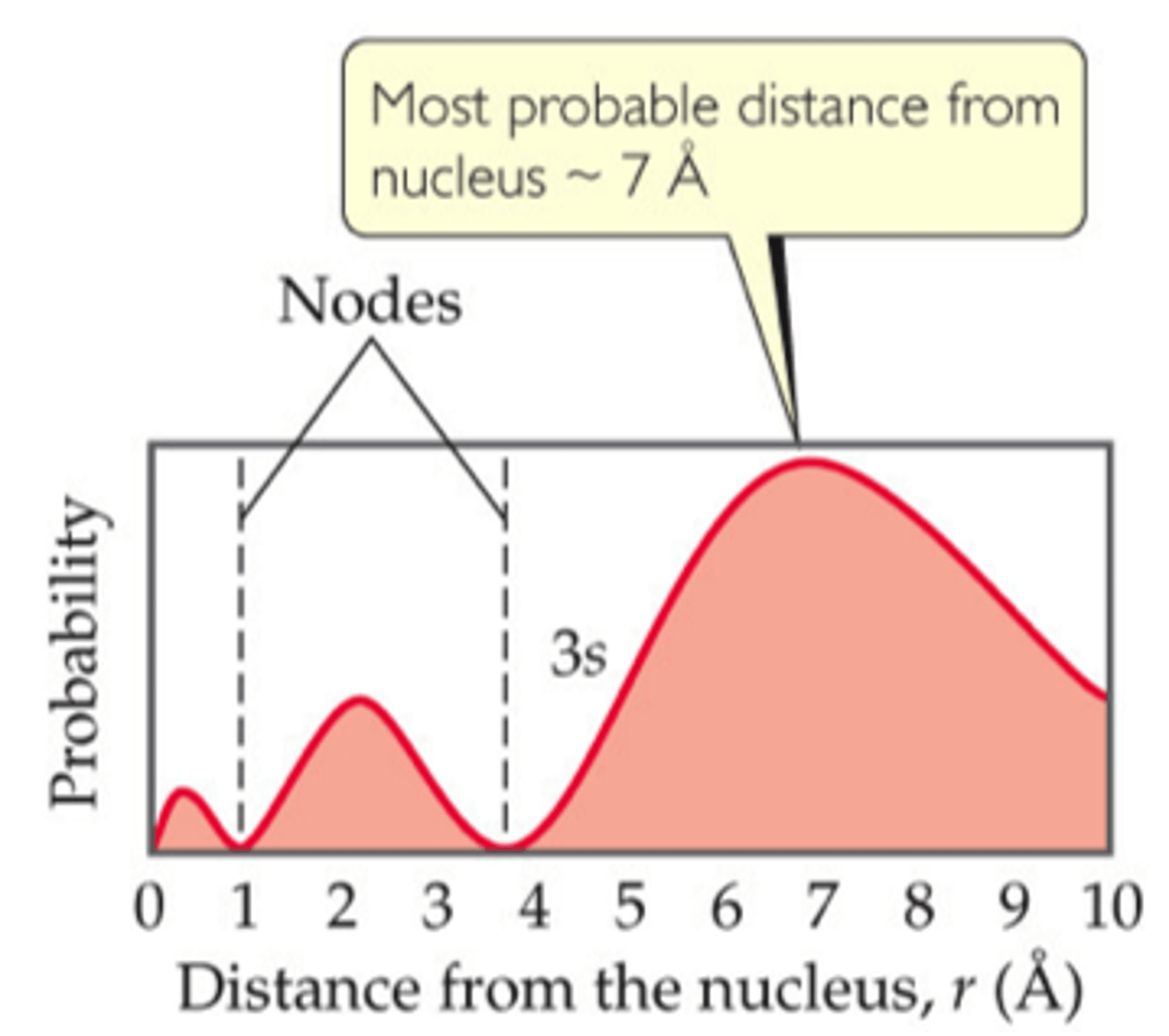
radial probability function

shows how far away an electron is likely to be from the nucleus

The number of peaks is equal to n. The outermost peak is the largest.

The number of nodes is equal to n-1.

As n increases, there is a greater probability that the electron is farther from the nucleus so the size of the orbital increases.

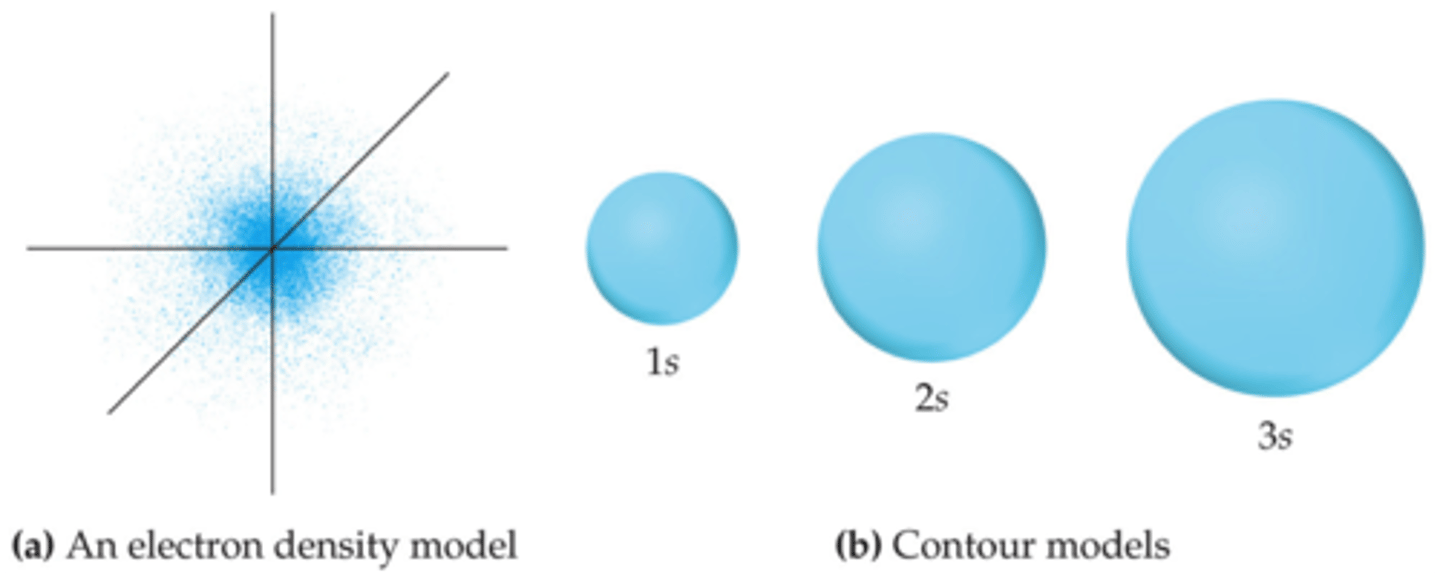
s orbital

spherically symmetric

each shell has one s orbital

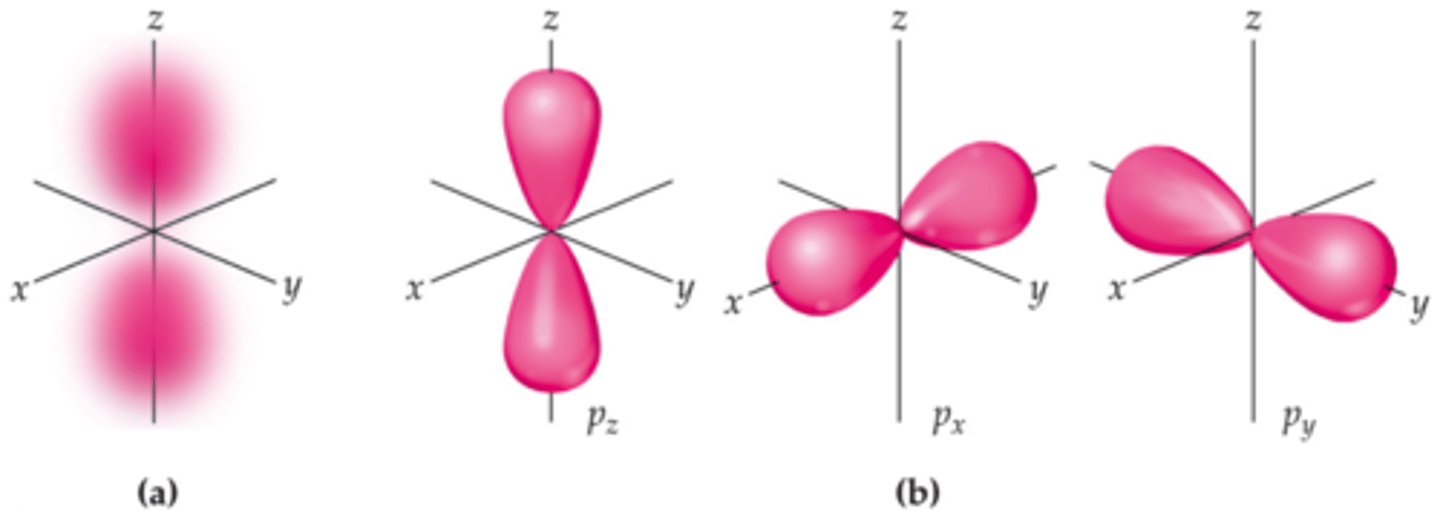
p orbital

dumbbell-shaped (two dense regions or lobes on either side of the nucleus with a node in the middle)

each shell with p orbitals has three p orbitals of the same size but different orientation

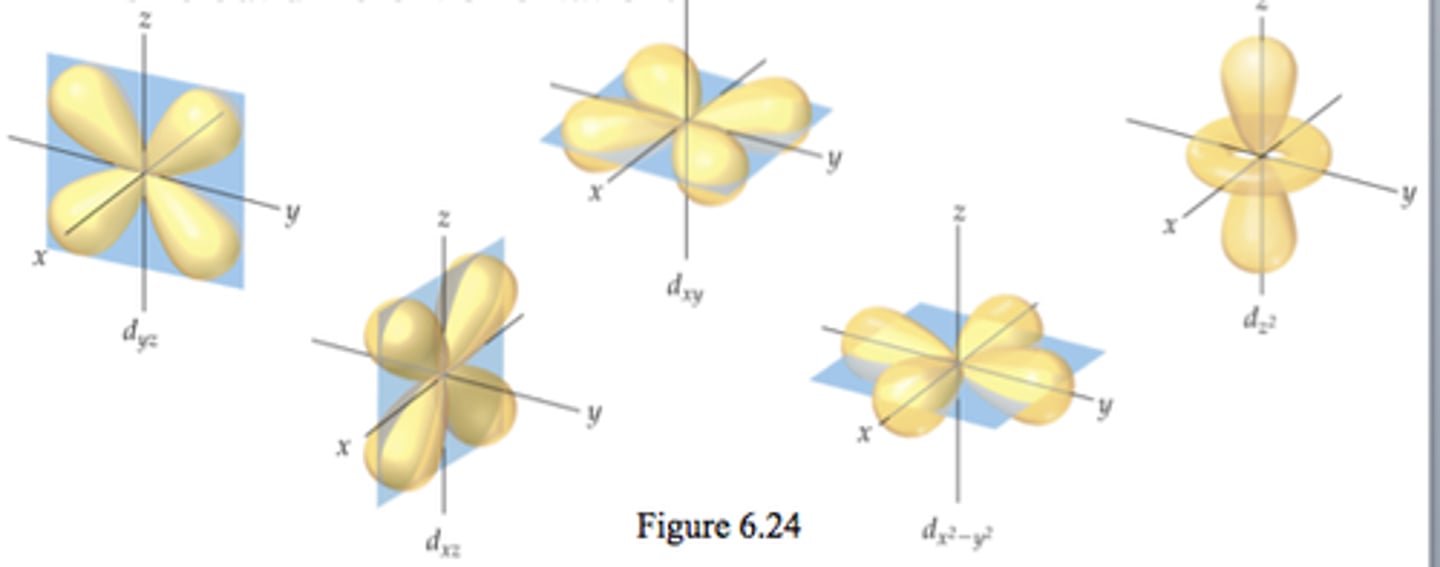
d orbitals

vary in shape

each shell with d orbitals has five d orbitals of the same size but different orientation

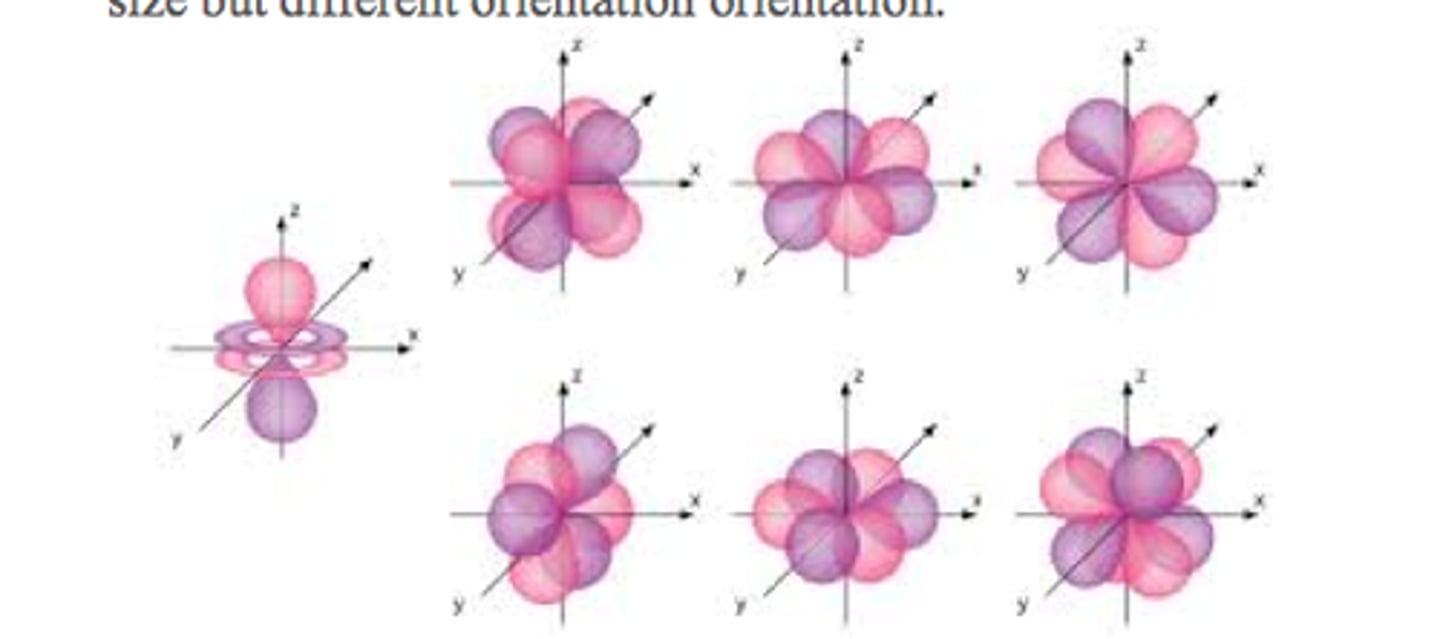
f orbitals

vary in shape

each shell with f orbitals has seven f orbitals of the same size but different orientation

representations of orbitals

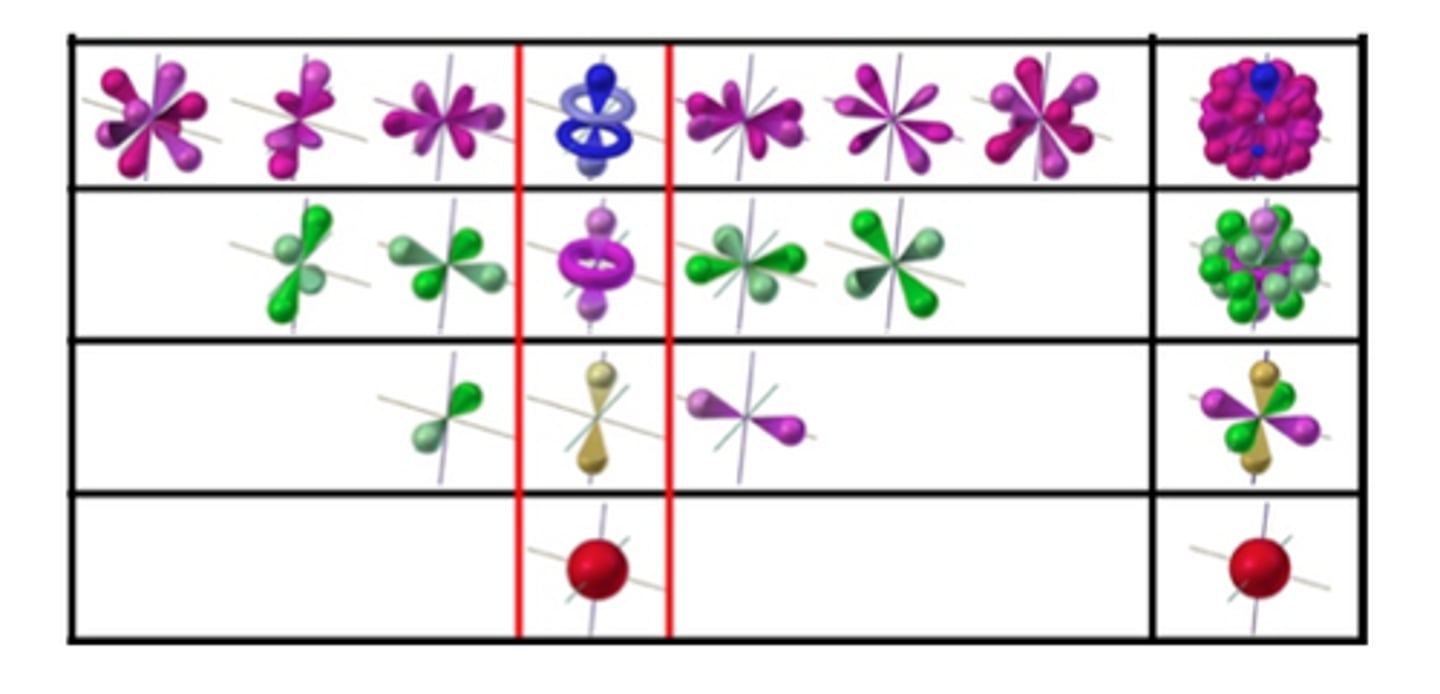
many-electron atoms

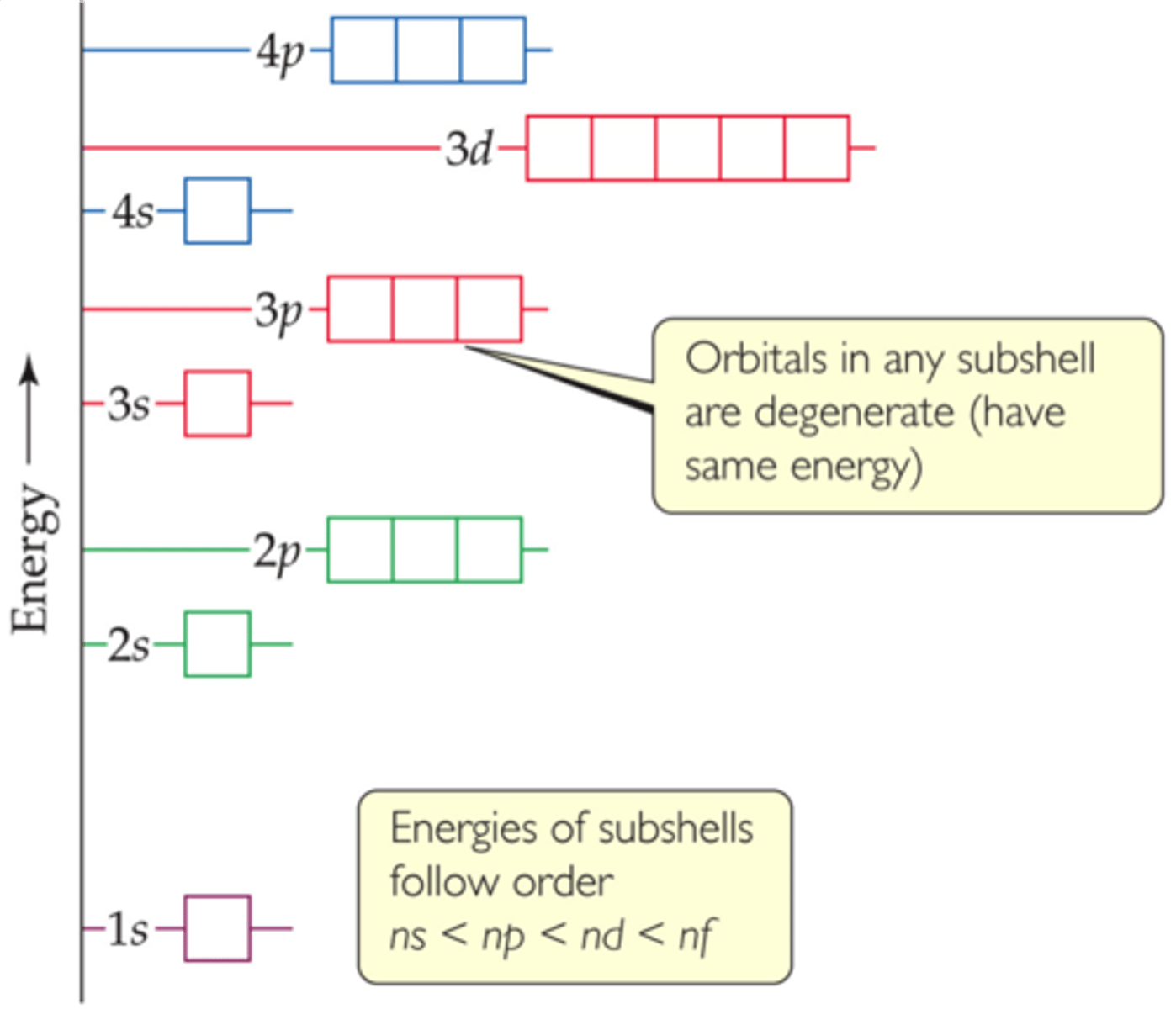
The electronic structure of many-electron atoms can be described by using the orbitals described for H, but their energies are different.

For a given n, the energy of an orbital increases with increasing l.

All orbitals in a given subshell have same energy and are said to be degenerate.

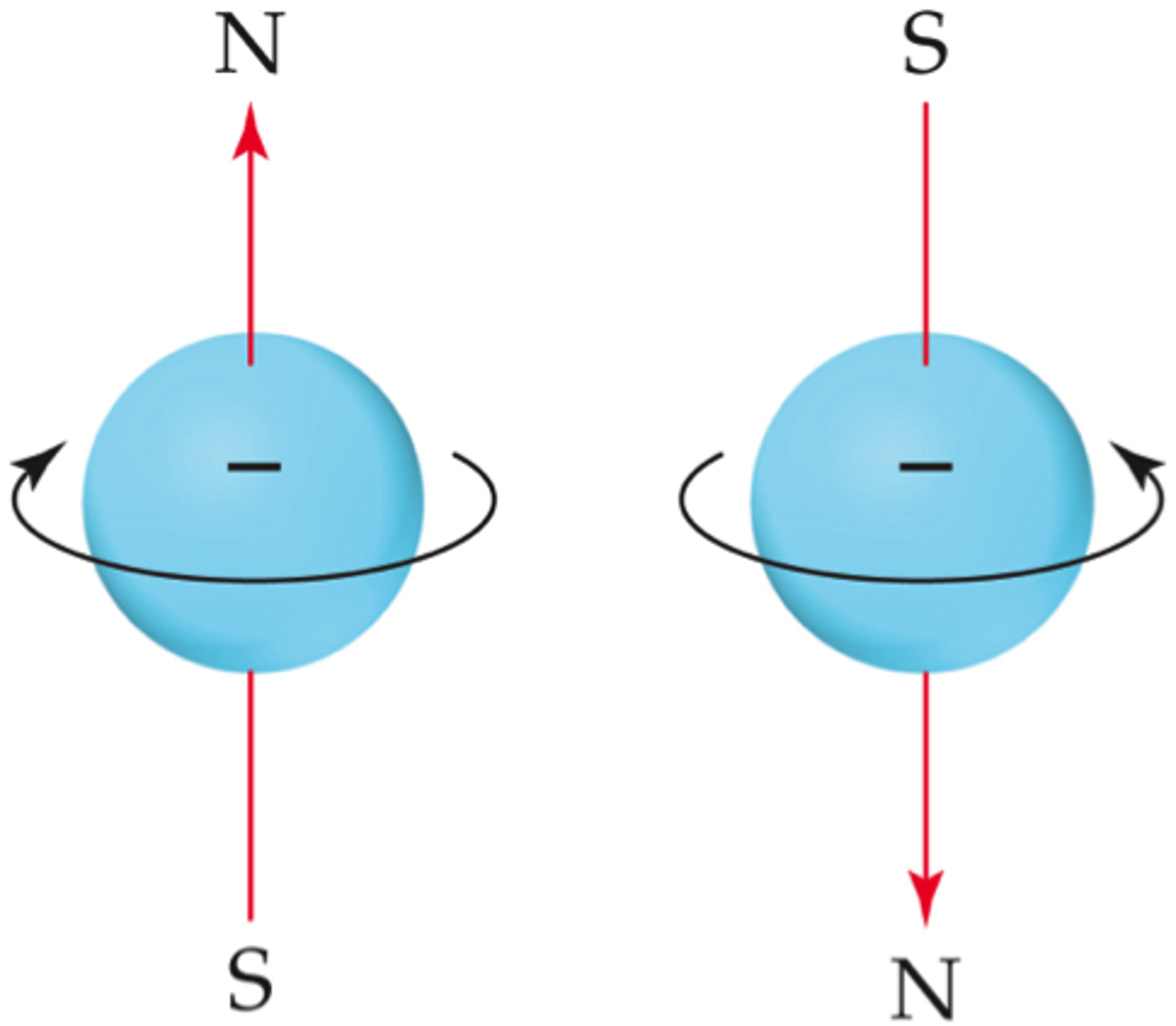
electron spin

intrinsic property of electrons to spin on its own axis; quantized value

ms = spin magnetic quantum number

values are +1/2 and -1/2

Pauli exclusion principle

states that no two electrons in an atom can have the same set of four quantum numbers

for a given orbital, n, l, and ml are fixed; only ms can change

actual important part: therefore an orbital can hold a maximum of two electrons with must have opposite spins

electron configuration

distribution of electrons among that various orbitals

orbitals filled in order of increasing energy with no more than 2 electrons per orbital

ground state for many-electron atoms

orbital diagrams

used to represent electrons configurations

paired electrons have opposite spins and occupy the same orbital

unpaired electron in a lone electron in an orbital

Hund's rule

first they fill up orbitals before they pair up

core electrons

inner shell electrons and are equivalent to the electron configuration of the preceding noble gas

outer shell electrons

those listed after noble gas

valence electrons

outer shell electrons involved in chemical bonding