Computer Graphics Midterm

What distinguishes an Affine Space from a Vector Space?

An Affine Space adds the concept of points to a vector space, allowing for the definition of a coordinate system origin.

What concept do Euclidean Spaces add to Affine Spaces?

Euclidean spaces add metrics for measurement, such as distance and length, and define operations like the dot and cross product.

What are the two defining properties of vectors in a vector space?

Vectors have both magnitude and direction.

In vector addition, the _____ axiom is used to combine vectors geometrically.

head to tail

What is the result of a dot product of two vectors?

The result is a scalar value.

What is the geometric significance of the cross product of two vectors?

The resulting vector is orthogonal (perpendicular) to the plane containing the two input vectors.

In computer graphics, what is a primary application of the vector cross product?

Calculating the normal vector to a surface or polygon.

The formula ∣x∣∣y​∣cosθ calculates the _____ of vectors x and y​.

dot product

What fundamental property of matrix multiplication is not always true, unlike scalar multiplication?

Matrix multiplication is not commutative; in general, A⋅B != B⋅A.

What is the primary motivation for using homogeneous coordinates in computer graphics?

To represent all affine transformations, including translation, as a single matrix-vector multiplication.

How is a 2D point (x,y) represented in homogeneous coordinates?

It is represented as (x,y,w), where the projection to 2D is typically on the w=1 plane, resulting in (x,y,1).

In homogeneous coordinates, what distinguishes the representation of a vector from that of a point?

A point has a non-zero w coordinate (typically 1), while a vector has a w coordinate of 0.

What is the general matrix-vector equation for a 2D affine transformation without homogeneous coordinates?

Q​=MP+T

What two geometric properties are always preserved by affine transformations?

Affine transformations preserve lines and the parallelism of lines.

What two geometric properties are generally not preserved by affine transformations?

Distances between points and angles between lines are not preserved.

What is the 2D translation matrix in homogeneous coordinates for a translation by (T_x,T_y​)?

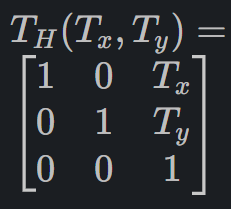
What is the 2D scaling matrix in homogeneous coordinates for scaling by (S_x,S_y​)?

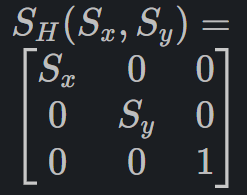
What is the 2D rotation matrix in homogeneous coordinates for a counter-clockwise rotation by angle θ?

R_H(θ)=​

[cosθ  −sinθ  0]

[sinθ    cosθ  0]

[  0         ​0     1​​]

What is the key advantage of being able to compose multiple affine transformations into a single matrix?

It is computationally efficient, as the composite matrix only needs to be calculated once to transform a large number of vertices

What is the sequence of transformations to rotate an object by angle θ about an arbitrary point (x_r ,y_r​)?

1. Translate by (−x_r​,−y_r).

2. Rotate by θ. 3. Translate back by (x_r ​,y_r​).

The composite transformation matrix M for rotating about point (x_r ,y_r​) would be the product M=T(x_r ,y_r​)⋅R(θ)⋅T(−x_r ,−y_r​). In what order are these matrices applied to a vertex vector P?

The matrices are applied from right to left: M⋅P=(T(x_r ​,y_r​)⋅R(θ)⋅T(−x_r ,−y_r))⋅P.

What is the inverse of a translation transform T(T_x ,T_y​)?

The inverse is T^-1(T_x ,T_y)=T(−T_x ​,−T_y​).

What is the inverse of a scaling transform S(S_x ​,S_y​)?

The inverse is S^-1(S_x ,S_y​)=S(1/S_x ​,1/S_y​).

How does transforming an object's points by matrix M relate to transforming the coordinate system by matrix M?

They are duals; transforming points by M is equivalent to transforming the coordinate system by M^-1.

In 3D graphics, what are the dimensions of the homogeneous transformation matrices?

They are 4x4 matrices.

A _____ transformation can be described as a translation along one dimension that is a linear function of another dimension's coordinate.

shear

What is the general 2D matrix for an X-axis shear transformation?

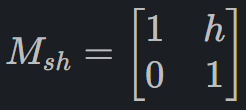
What distinguishes geometric primitives from raster primitives in the graphics pipeline?

Geometric primitives (points, lines, polygons) pass through the geometric pipeline, while raster primitives (pixel arrays, textures) pass through the texture pipeline

Why is triangulation a common solution for rendering polygons in 3D?

It ensures that polygons are simple, flat (planar), and convex, which simplifies and guarantees correct rendering by hardware that is optimized for triangles.

What is a 'triangle strip' primitive?

A sequence of connected triangles where each new vertex, after the first two, defines a new triangle with the previous two vertices, making it vertex-efficient.

In the parametric representation of a line segment from point P0​ to P1​, what is the equation for a point on the line?

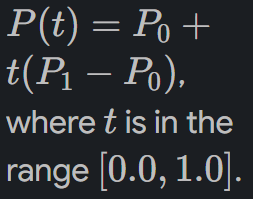
What is the difference between Stroke Text and Raster Text?

Stroke text is defined by geometric primitives (lines/curves) and is scalable, while raster text is defined by pixels and does not scale well.

What are 'attributes' in the context of computer graphics?

Attributes are properties that define how a geometric primitive is to be rendered, such as color, line style, or texture.

What type of light-sensing cells in the human retina are responsible for color vision?

Cone cells are responsible for color vision.

What type of light-sensing cells in the human retina account for night vision (low-light sensitivity)?

Rod cells account for night vision.

The human visual system's tristimulus response means it is most sensitive to which color of light?

It is most sensitive to green light.

The _____ color model is used for displays and involves adding red, green, and blue light together.

additive

The _____ color model is used for printing and involves cyan, magenta, and yellow pigments that remove color components from a white surface.

subtractive

What is the purpose of the 'alpha channel' in a 32-bit RGB color system?

The alpha channel stores transparency or opacity information for each pixel.

What is the fundamental difference between parallel and perspective projections?

In parallel projection, projectors are parallel to each other, while in perspective projection, projectors converge at a single point (the center of projection).

Which type of projection maintains the relative proportions of objects regardless of their distance from the camera?

Parallel (orthographic) projection.

The synthetic camera model in computer graphics places the image plane _____ of the viewer, unlike a real-world camera.

in front

What three components are specified in world coordinates to define a camera's position and orientation?

A view reference point (VRP or camera position), a view plane normal (VPN or look-at direction), and an up vector (UP).

What is the purpose of the camera transformation in the 3D viewing pipeline?

It transforms object vertices from world coordinates into a new coordinate system where the camera is at the origin and looking down a specific axis (e.g., -Z).

The overall transformation from an object's model coordinates to the final projected 2D coordinates is represented by the matrix product M=M_Proj ⋅ M_mv. What do M_Proj and M_mv represent?

M_Proj is the projection transformation, and M_mv is the model-view transformation, which combines the model and camera (view) transforms.

In the context of the 3D viewing pipeline, what is the 'view volume' or 'frustum'?

It is the region of 3D space that is visible to the camera and will be mapped to the screen.

The camera transformation is composed of a translation and a rotation. What is the purpose of the translation component?

To translate the camera's position (VRP) to the origin of the world coordinate system.

The camera transformation's rotation component aligns the camera's basis vectors (U,V,N) with which world axes?

It aligns them with the world's primary axes (X,Y,Z), i.e., ((1,0,0),(0,1,0),(0,0,1))

Given a look-at direction vector LAT and an up vector UP, how is the camera's rightward-pointing vector U typically calculated?

It is calculated using the cross product: U=LAT′×UP′, where the vectors are normalized.

What is the primary role of a Graphics Processing Unit (GPU) in modern graphics systems?

The GPU performs all vertex and fragment processing, rasterization, and framebuffer updates using massive parallelism for high throughput.

A _____ image is organized as a 2D array where each addressable location corresponds to one pixel.

raster

What does 'bit depth' or 'bit planes' refer to in the context of a raster image?

It is the number of bits used to store information (like color) for each pixel.

The process of approximating curved surfaces with a mesh of polygons is known as _____.

tessellation (or triangulation)

What is the term for a polygon where a line segment connecting any two points inside the polygon lies entirely within the polygon?

A convex polygon.

What is the matrix for reflecting a 2D point across the Y-axis?

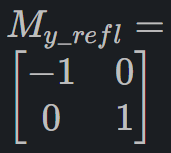
What is the matrix for reflecting a 2D point across the X-axis?

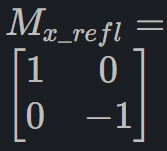
What is the sequence of primitive transformations that make up the 'Window to Viewport' transform?

1. Translate window to origin.

2. Scale window to unit size.

3. Scale to viewport size.

4. Translate to viewport origin.

In a modern graphics hardware pipeline, the stage that determines the final color of each pixel is called the _____.

fragment shader (or fragment processing)

What is 'double buffering' in graphics systems?

Using two sets of framebuffers; one is used for drawing the next frame while the other is being displayed, then they are swapped to prevent tearing.

What is the purpose of the 3D clipping stage in the viewing pipeline?

It removes any geometry that lies outside the defined view volume (frustum) so it isn't processed further.

The general trade-off in computer graphics applications is often between speed and _____.

realism

What is the first step in the procedure for rotating an object around an arbitrary axis in 3D?

Translate the object so that the arbitrary axis passes through the origin.

The 3D rotation matrix for rotation around the Z-axis by angle θ is ?

The 3D rotation matrix for rotation around the X-axis by angle θ is?

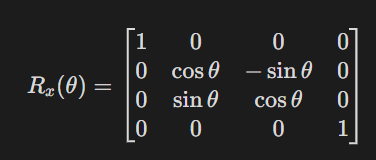
In a vector space, a set of n linearly independent vectors in an n-dimensional space is called a _____.

basis

Any vector can be written as a unique linear combination of _____ vectors.

basis

What defines a 'frame' in an affine space?

A frame is determined by an origin point and a set of basis vectors.

In the 3D viewing pipeline, the transformation from model coordinates to world coordinates is the _____ transform.

model

The projection transformation in the 3D pipeline maps the view volume into a _____.

canonical view volume (typically a unit cube)