Marine Fisheries Quiz #4

Fecundity

Batch Spawning

Growth

Indeterminate

Mortality

Type III Curve

Maximum Age

Variable and Dependent on environment

AFR

Age at First Reproduction: Variable with latitude, critical life history characteristic for exploitation.

Affected by growth, density, and food availability.

Recruitment

Addition of new individuals to the fishable portion of the stock.

Meristics

Structure counts (fins)

Morphometrics

Shape differences

Parasite Load

Parasites from migrating species

Biochemical

Electrophoresis, allozymes, DNA

Isotopes

Composition of otolith aragonites to determine age.

Density-Dependent

Competition, predation, disease, spawning sites.

Density-Independent

Weather, temperature.

Year-Class Strength

Influenced by survival and recruitment of hatchlings.

Depensatory Mortality

Population decline due to low stock size.

Indeterminate Growth

Growth continues after sexual maturity.

Age Determination

Otoliths: Count annuli for age.

Back-Calculation: Fraser-Lee.

Cohort

Group of individuals within a stock spawned at the same time.

Age Class

Used to determine length-at-age.

Fraser-Lee Model

L_i = [((L_c – a)/OR_c) OR_i ] + a

Lee’s Phenomenon

Older individuals back-calculate smaller at young ages than reality of young individuals.

Von Bertalanffy Model

L_t = L_∞[1-e^{-K(t-t  )}]

Protogynous Hermaphrodite

Female to male. (Yellowfin Grouper)

Length-Weight Power Function

W = aL^b

logW = log(a) + b(logL)

Isometric Growth

Shape of fish does not change. L/W=3

Allometric Growth

Fish grow thinner of heavier. L/W=<3<

Match/Mismatch

Food availability and spawning do not line up due to asynchronous life history changes effecting recruitment and growth.

Compensatory Effects

Higher growth response due to stunted fish seed. Not as strong as expected.

Protect BOFFFF

They enhance stock productivity.

Exponential Decay Model

N_t = N_oe^-Zt

A

Simple Mortality: Percentage of fish dying in a given time.

S

Survival: Complement of A.

Instantaneous Mortality Model

Z= -lnS

Capture Model

C_t = qf_tN_t

Catch Curve

ln(N_t) = lnN_o - Zt     

 

-ln(N_t) = Y

-t = X

Large Representative Sample

Age Key

Ranking of fish ages used to assess population dynamics, growth rates, and life history strategies.

Assumptions of Catch Curve

Stable age structure, consistent recruitment, mortality, and catchability.

Year-Class Strength Variability

-Boom v. Bust years

-r-selected species fluctuate in YCS

How to Minimize Variability

-Eliminate anomalous year-classes

-Average Z for several successive years

-’Average Catch Curve’

John Hoenig

  ln(Z) ~ 1.44 - 0.982 ln(t_max), r²=0.82

-Unexploited stocks

Natural Mortality Before Fishing Impact

 Z = M + qf  

r²

Variability in Y explained by X.

J.G. Shepherd Recruitment Model

R = aS  / 1 + (bS)^c

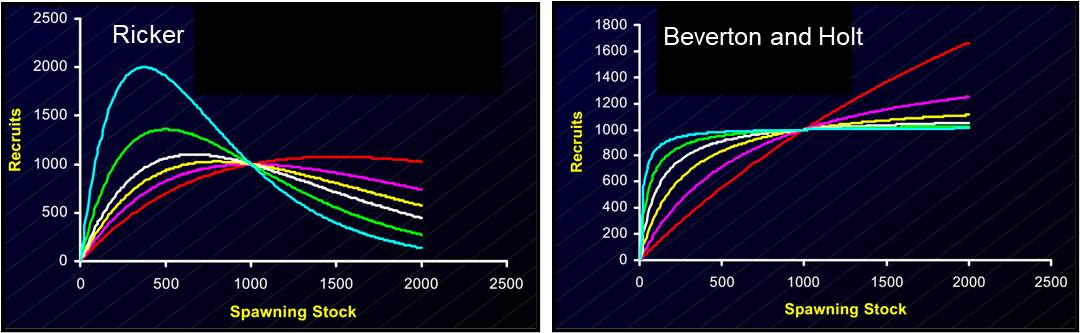
Ricker (1954)

High stock sizes lead to increased juvenile mortality.

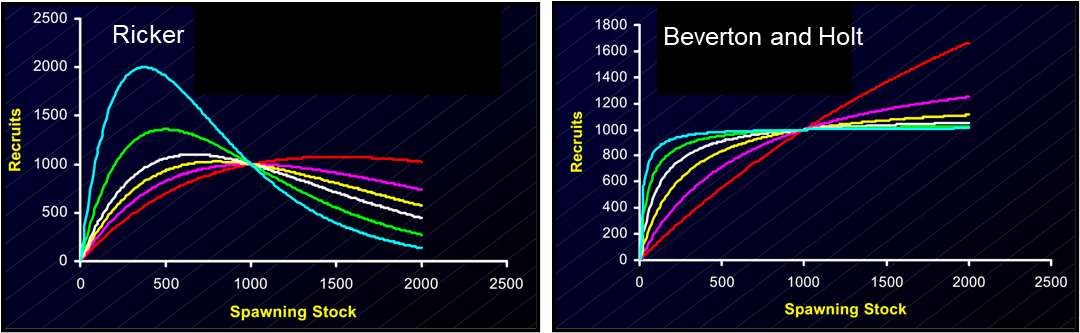
Beverton-Holt (1957)

Competition among juveniles limits mortality.

Allee Effect

Recruitment drops at low spawner abundance due to difficulty in finding mates, lack of spawning cues for group spawners, ineffective schooling behavior for anti-predator defense.

Challenges in Recruitment Modeling

Reality is much more complex so modeling is unrealistic.