Important Things to Know (Calc. AB)

Limit Properties

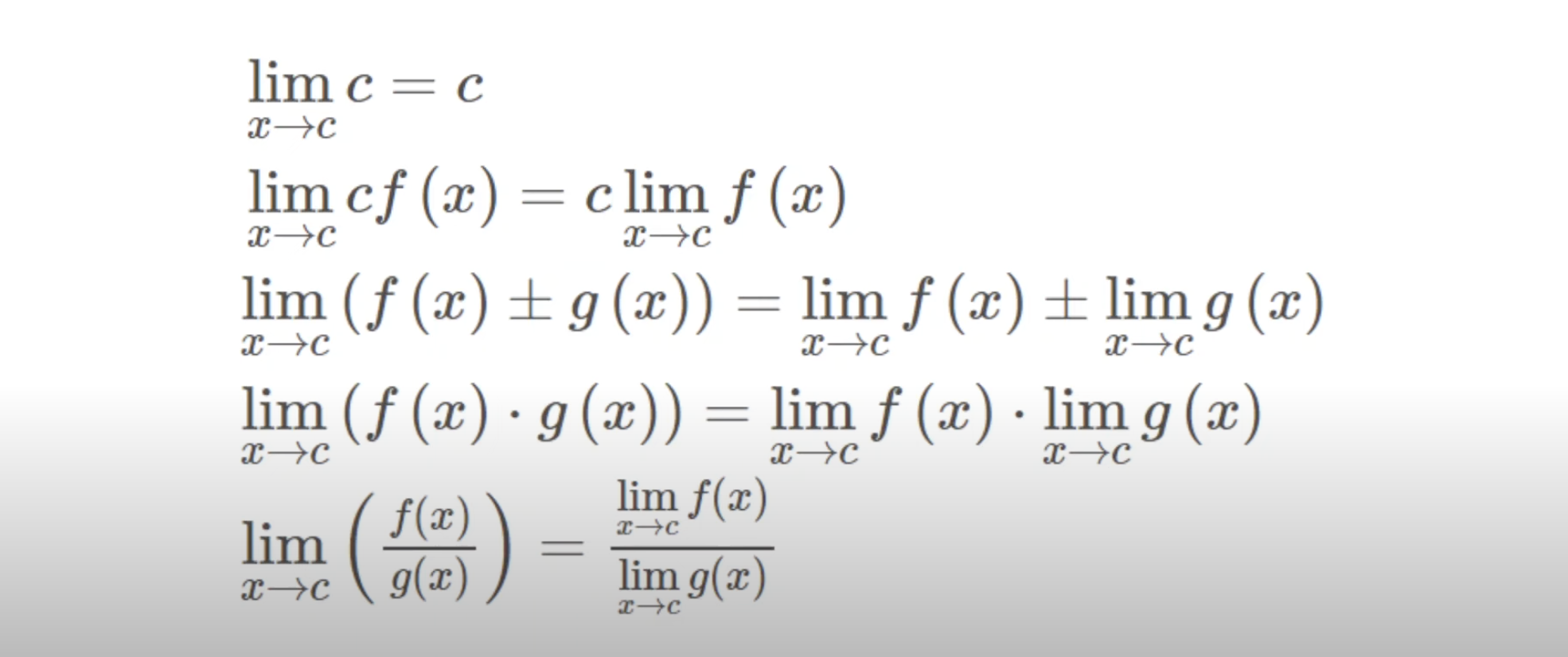
Trig. Identities + Trig. Limits

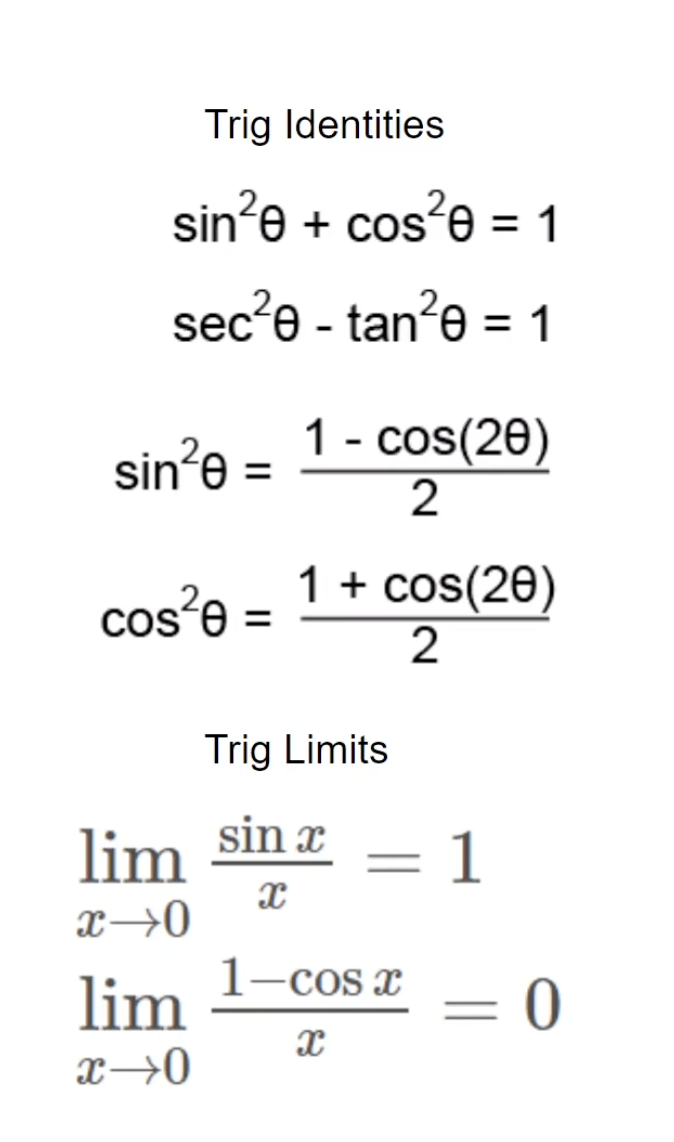
Squeeze Theorem

L’HOSPITAL’S RULE

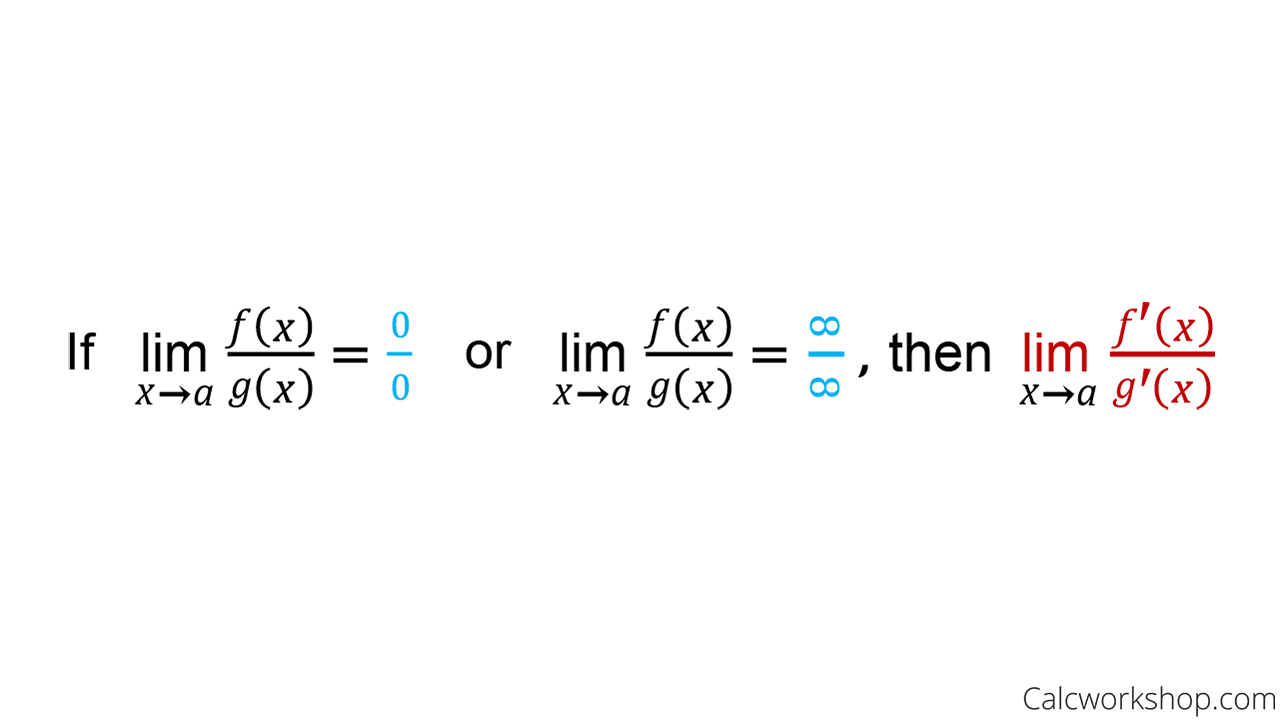
Criteria for Continuity

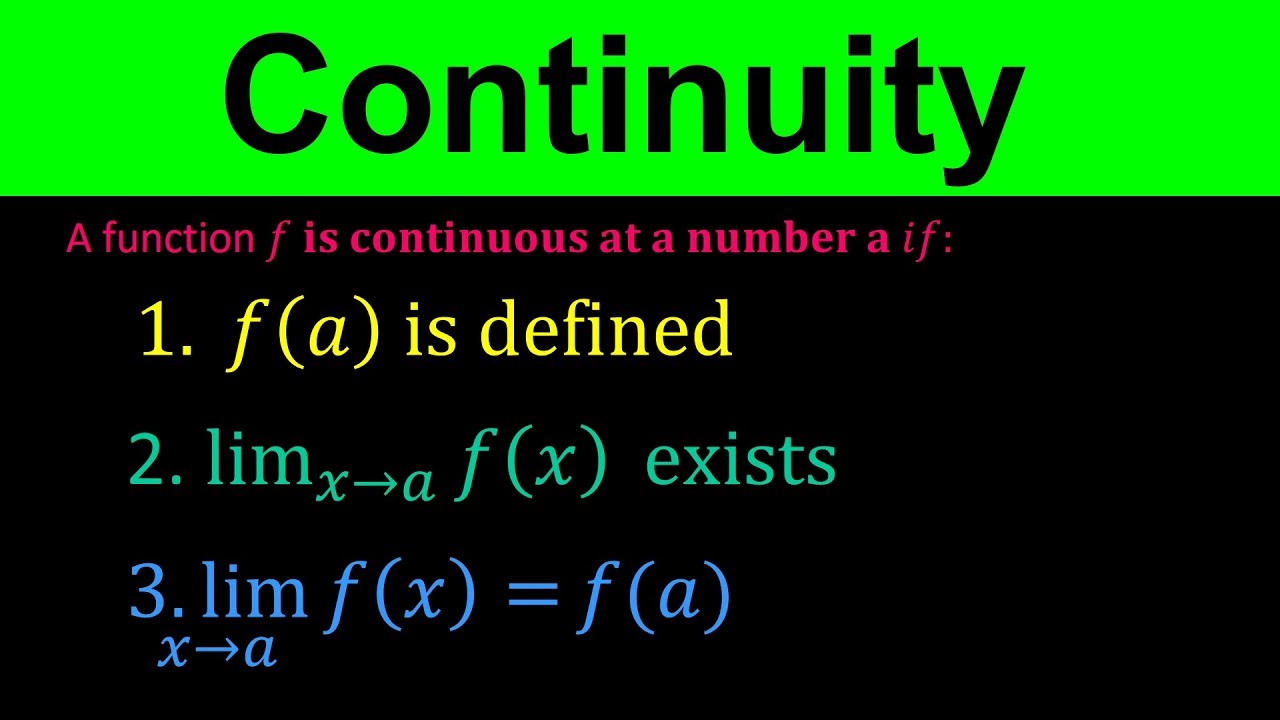
Types of Continuities

Holes occur when factors from the numerator and the denominator cancel (removable). When a factor in the denominator does not cancel, it produces a vertical asymptote (non-removable).

Horizontal Asymptote Rules + Vertical vs. Horizontal Asymptotes

Horizontal Asymptote Rules

If the degree of the den. > degree of num. = 0

If the degree of the den. = degree of num. = (leading coefficient)/(leading coefficient)

If the degree of the den. < degree of num. = no horizontal asymptote

Vertical vs. Horizontal Asymptotes

Vertical asymptotes occur where a function approaches infinity (limit), while horizontal asymptotes indicate a function's end behavior as x approaches infinity.

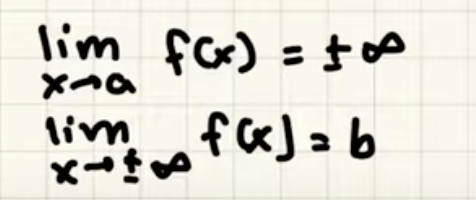
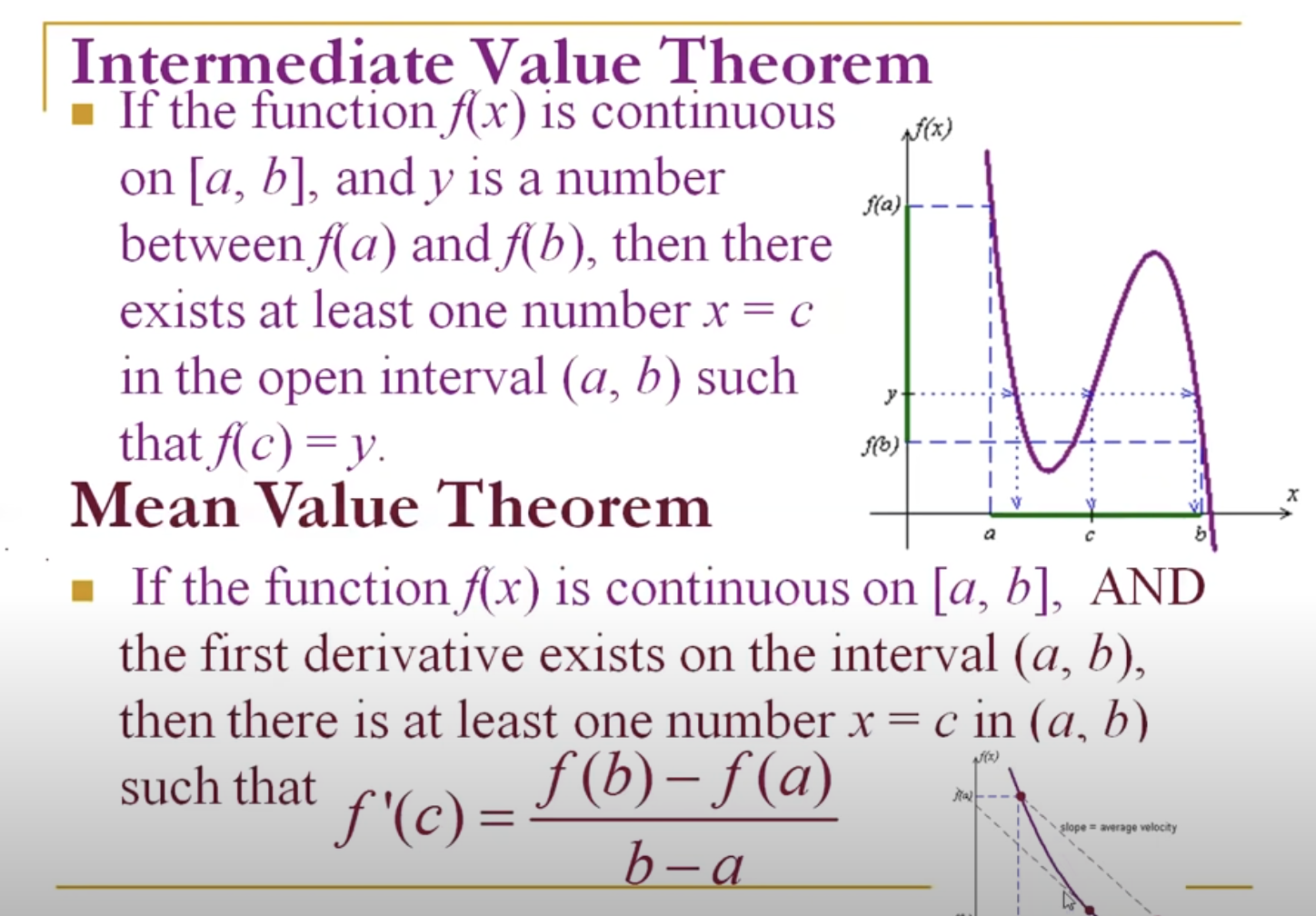
I.V.T. + M.V.T.

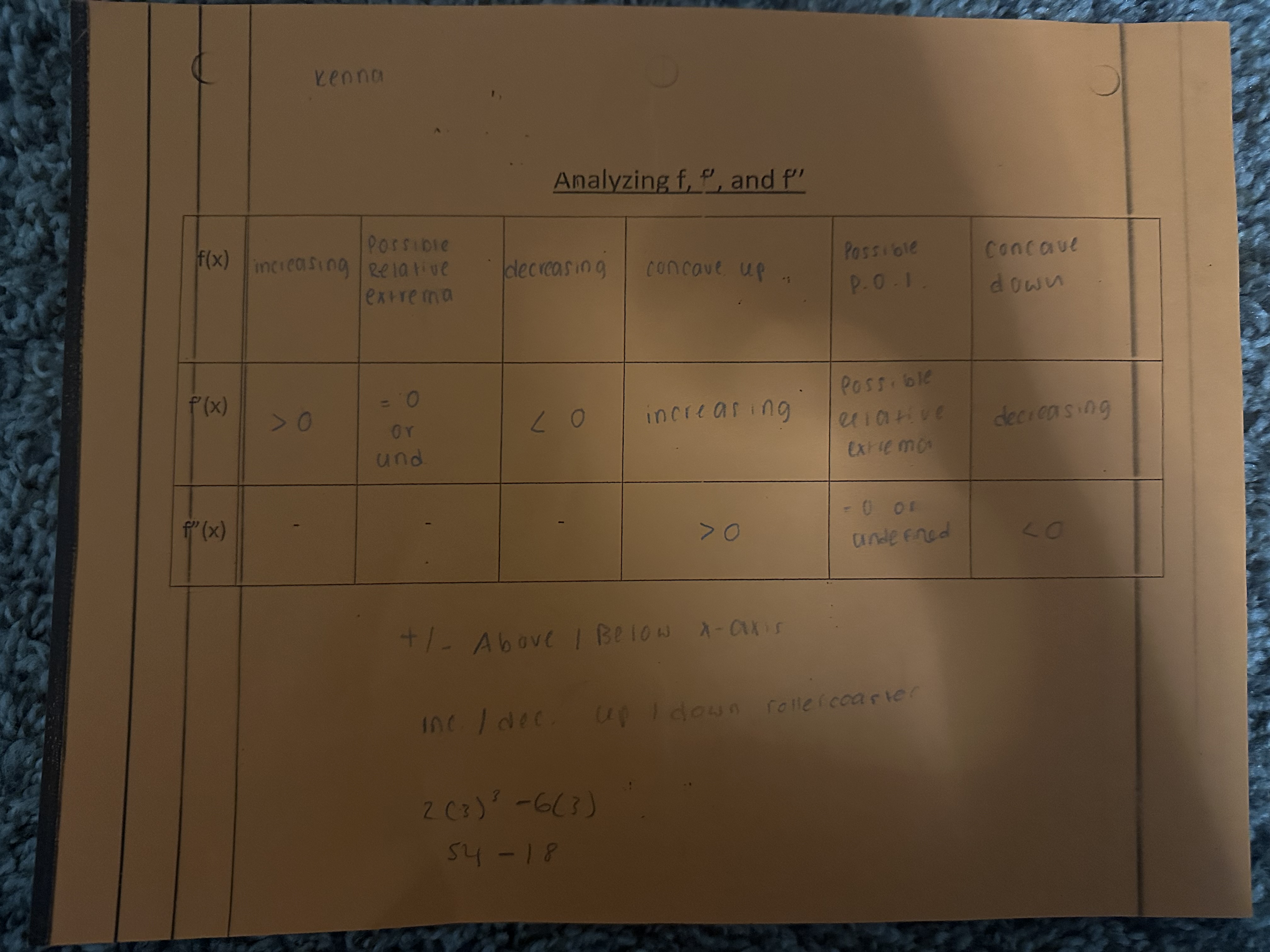
Curve Sketching

y = f(x) must be continuous at each:

• critical point: dy/dx = 0 or undefined and endpoints

• local minimum: dy/dx goes from - to + or d²y/d²x > 0

• local maximum: dy/dx goes from + to - or d²y/d²x < 0

• point of inflection: concavity changes

  • d²y/d²x changes sign

Basic Derivatives

Additional Derivatives

Basic Integrals

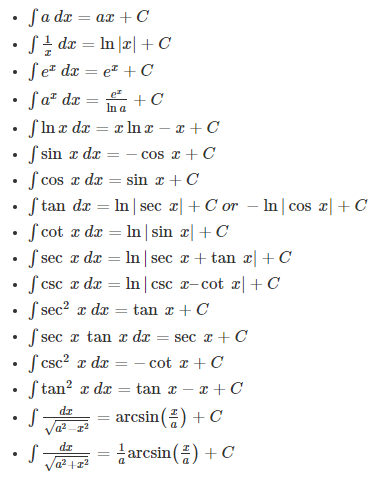
Integrating Inverse Trig. Functions

Differentiation Rules

Chain Rule: If y = f(g(x)), then y' = f'(g(x)) * g'(x).

Product Rule: If y = f(x) g(x), then y' = f'(x) g(x) + f(x) * g'(x)

Quotient Rule: If y = f(x) / g(x), then y' = [f'(x) g(x) - f(x) g'(x)] / [g(x)]² (lo de hi/hi de lo)/lolo

Fundamental Theorem of Calculus

Average Value

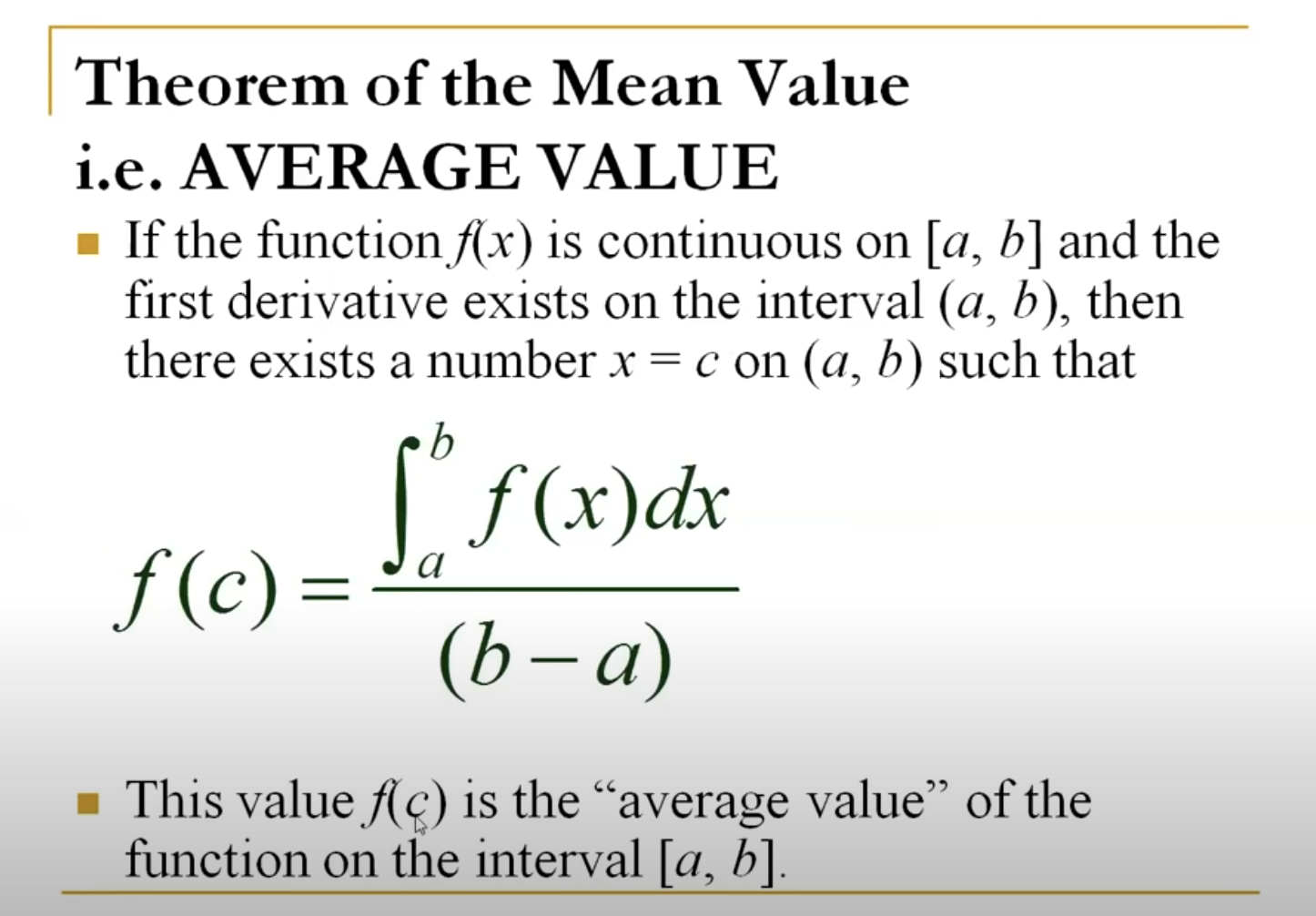
Volume Methods

Distance, Velocity, and Acceleration

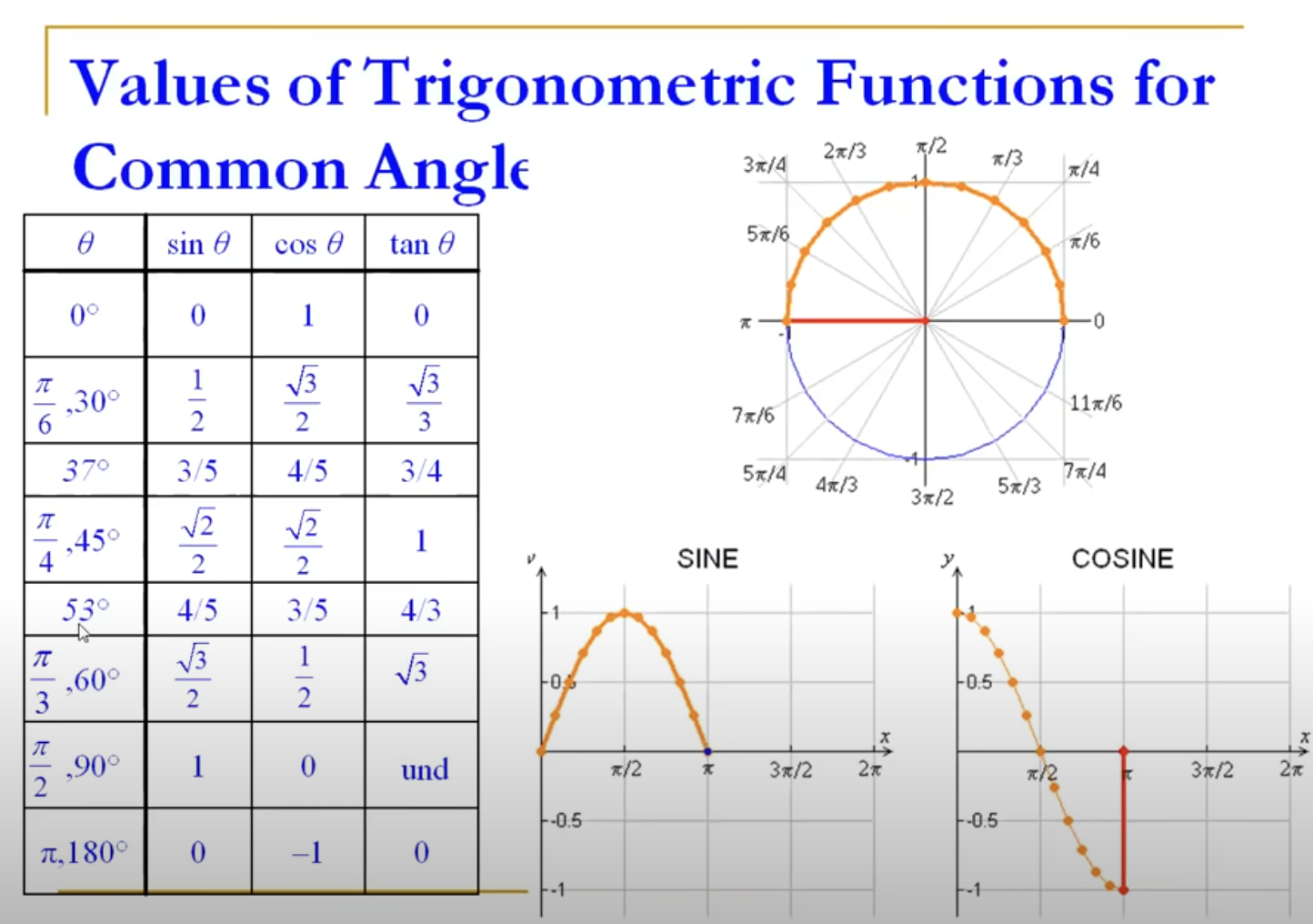
Values of Trig. Functions for Common Angles

Integration by Parts

Derivative of Inverse Functions

First Derivative, Candidate, Concavity, and Second Derivative Tests

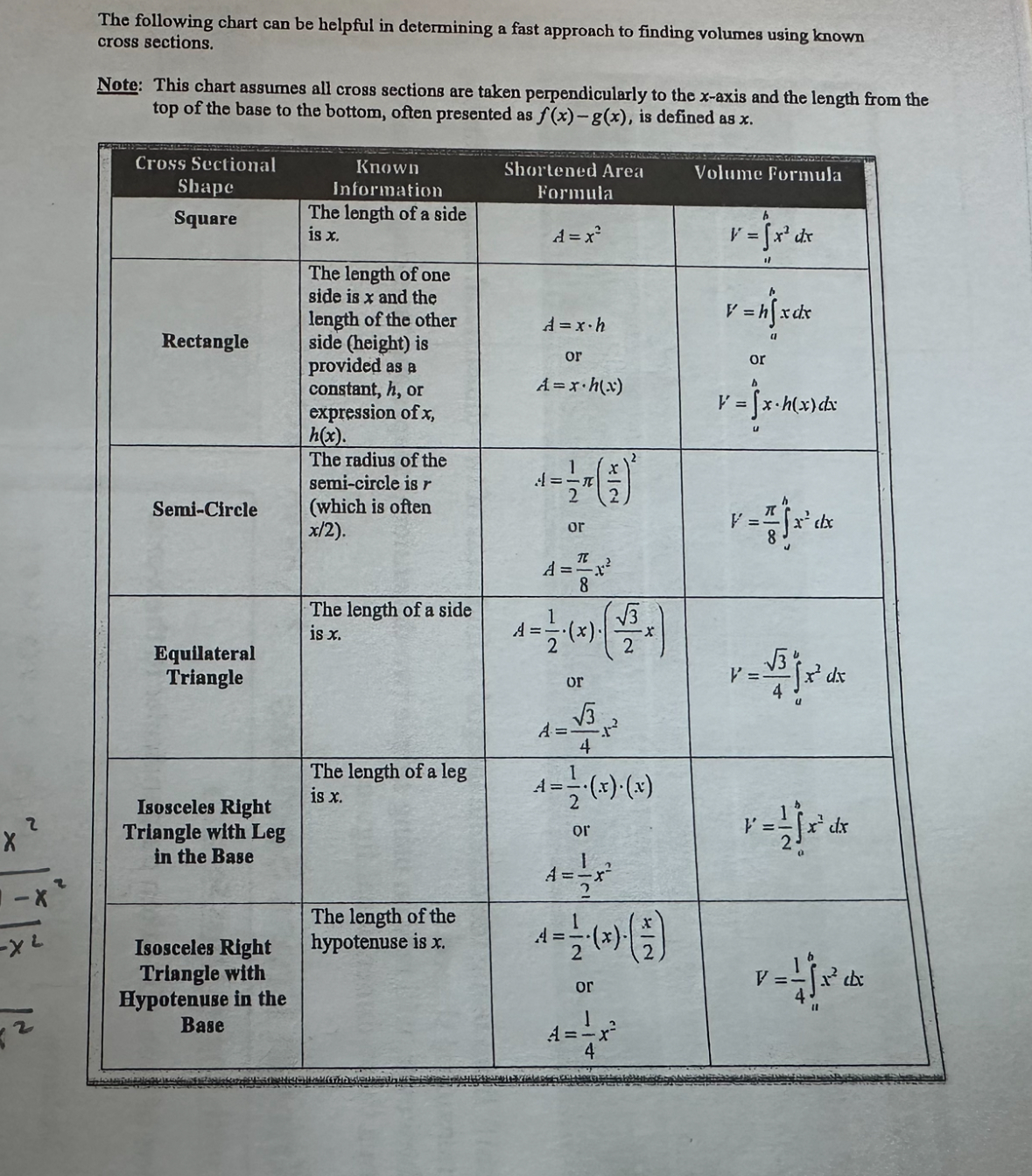
Cross Sections