AS level OCR Physics

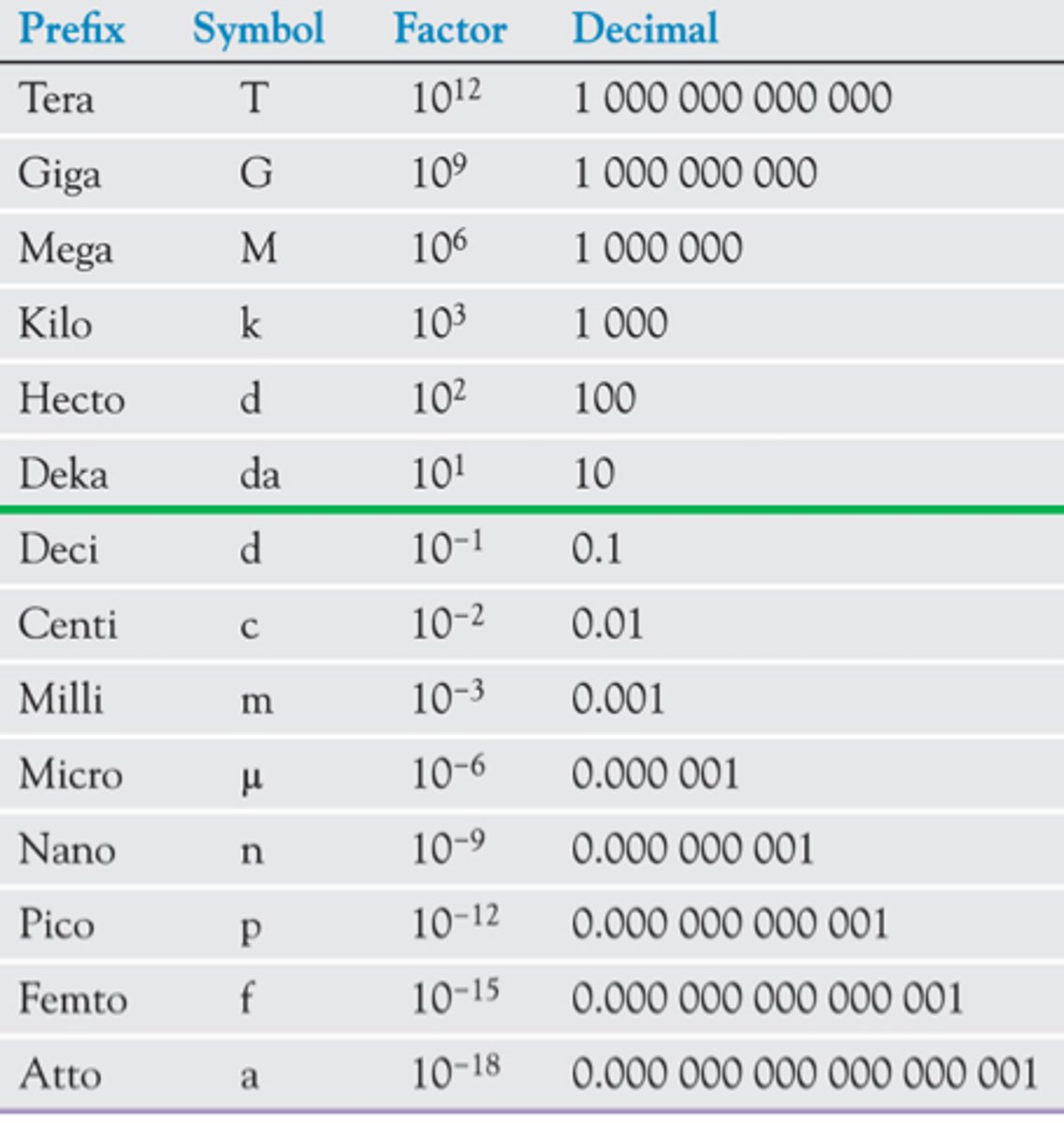
Prefix units

Uncertainties

Adding or subtracting- Add the absolute uncertainties

Multiplying or dividing- Add the percentage uncertainties

Raising to a power- Multiply the percentage uncertainties by the power

Percentage uncertainty in the gradient

uncertainty = ½(line of best fit - line of worst fit)

Percentage uncertainty = uncertainty ÷ gradient of best fit line (× 100)

Speed

Rate of change of distance

Displacement

The distance an object has travelled in a given direction

Velocity

Rate of change of displacement

Acceleration

Rate of change of velocity

Scalars

mass, time, temperature, speed, energy

Vectors

displacement, force, velocity, acceleration

Acceleration

Change in velocity divided by time

Displacement=

Average velocity × Time

Vertical velocity=

V × Sin θ

Displacement

Area under velocity-time graph

Time taken=

Number of frames × (1 second / frame rate)

Stopping distance=

Thinking distance + Braking distance

Inertia

Resistance to a change in velocity

Pressure=

h × ρ(density) × g

When the force isn't in the same direction as the movement

W= F × x × Cos θ

P= F × v × Cos θ

Power=

Force × Velocity

K.E.=

Work done

K.E.=

Force × Displacement

K.E.=

Mass × Acceleration × Displacement

Hooke's law

Force is proportional to extension

K

Force constant

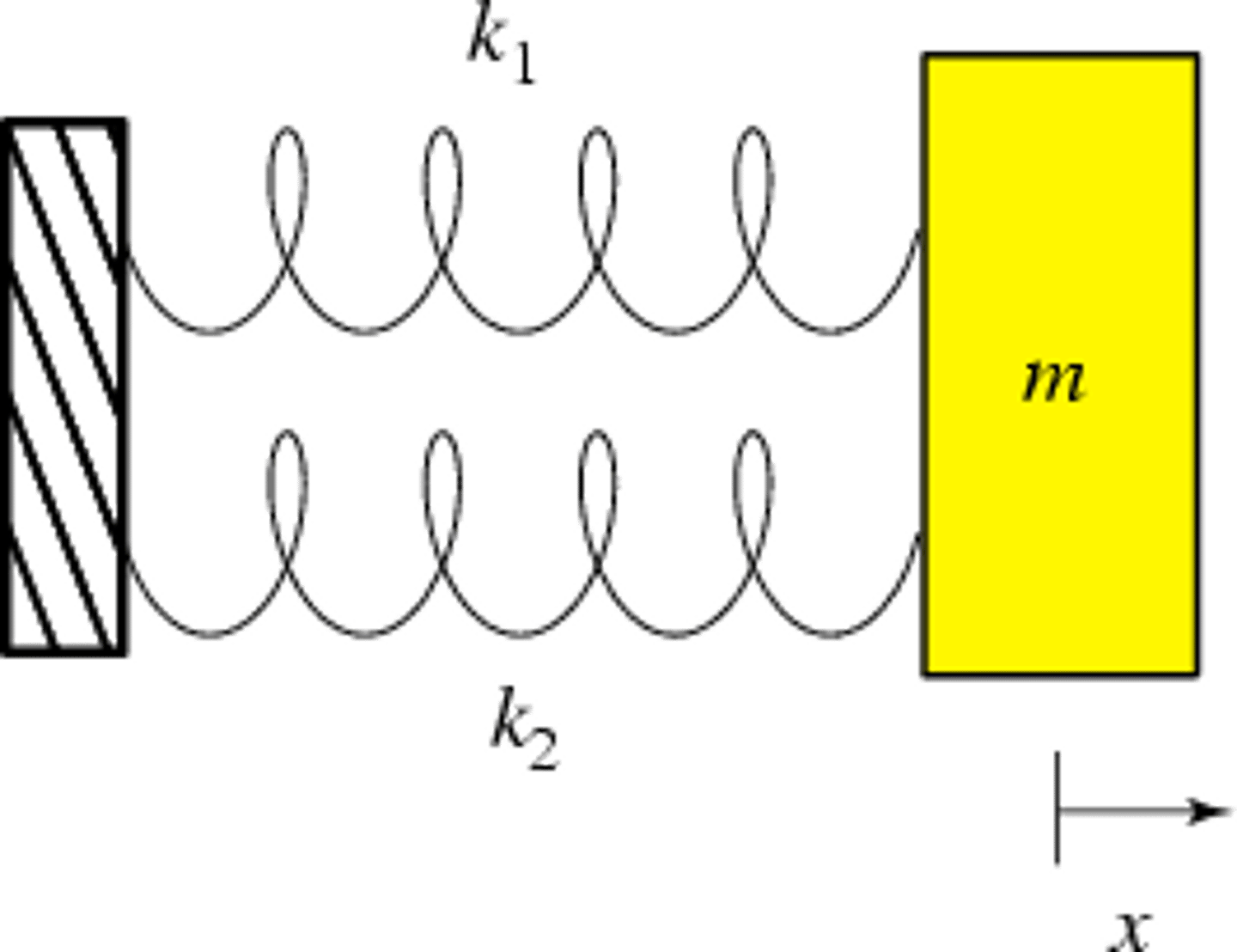
K in series

1/K = 1/K1 + 1/K2

K in parallel

K = K1 + K2

Tensile stress, σ=

Force / Area

Tensile strain, ε=

Extension / Length

Work done=

½ × F × x

Force=

K × x

Elastic potential energy=

½ × k × x²

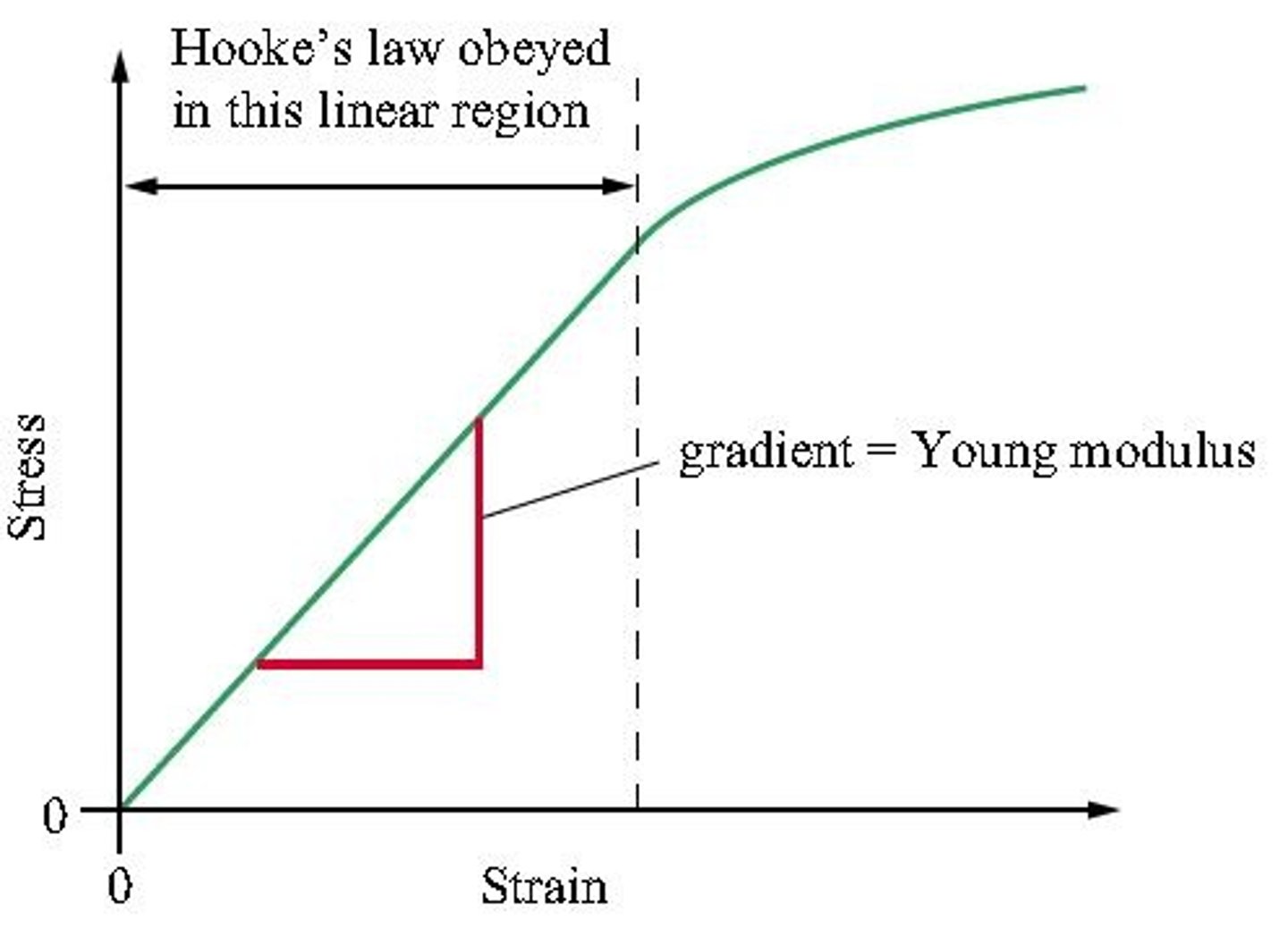
Young modulus=

Tensile stress / Tensile strain

Energy per unit volume=

½ × Stress × Strain

Limit of proportionality

The graph is no longer a straight line

The material stops obeying Hooke's law

Returns to its original shape if stress were removed

Elastic limit

The material behaves plastically

No longer returns to its original state if stress were removed

Yield point

Plastic deformation takes place with a constant or reduced load

The material stretches without any extra load

Conservation of momentum

Momentum before = Momentum after

Elastic collision

Momentum is conserved and kinetic energy is conserved

Inelastic collision

Momentum is conserved but some kinetic energy is lost

Impulse (Ns)

Change in momentum

F × ΔT

Newton's 1st law

Force is needed to change velocity

Newton's 2nd law

Force...

Rate of change of momentum

Change in momentum / Time

Newton's 3rd law

Each force has an equal, opposite reaction force

Current

Rate of flow of charge

One coulomb

The amount of charge that passes in one second when the current is one ampere

Potential difference

Work done per unit charge

One volt

The p.d. is one volt when you do one joule of work moving one coulomb of charge

1 V = 1 J / C

Current=

Anev

One ohm

If a p.d. of one volt makes a current of one amp flow through the component

Resistivity (Ohm metres)

The resistance of a 1m length with a 1m² cross-sectional area

Resistivity=

RA / L

Power=

V × I

Work done=

VI × T

Power × Time

e.m.f, ε=

V + v

The total amount of work the battery does on each coulomb of charge

Resistance in series

Total R = R1+ R2 + R3

Resistance in parallel

1/Total R = 1/R1 + 1/R2 + 1/R3

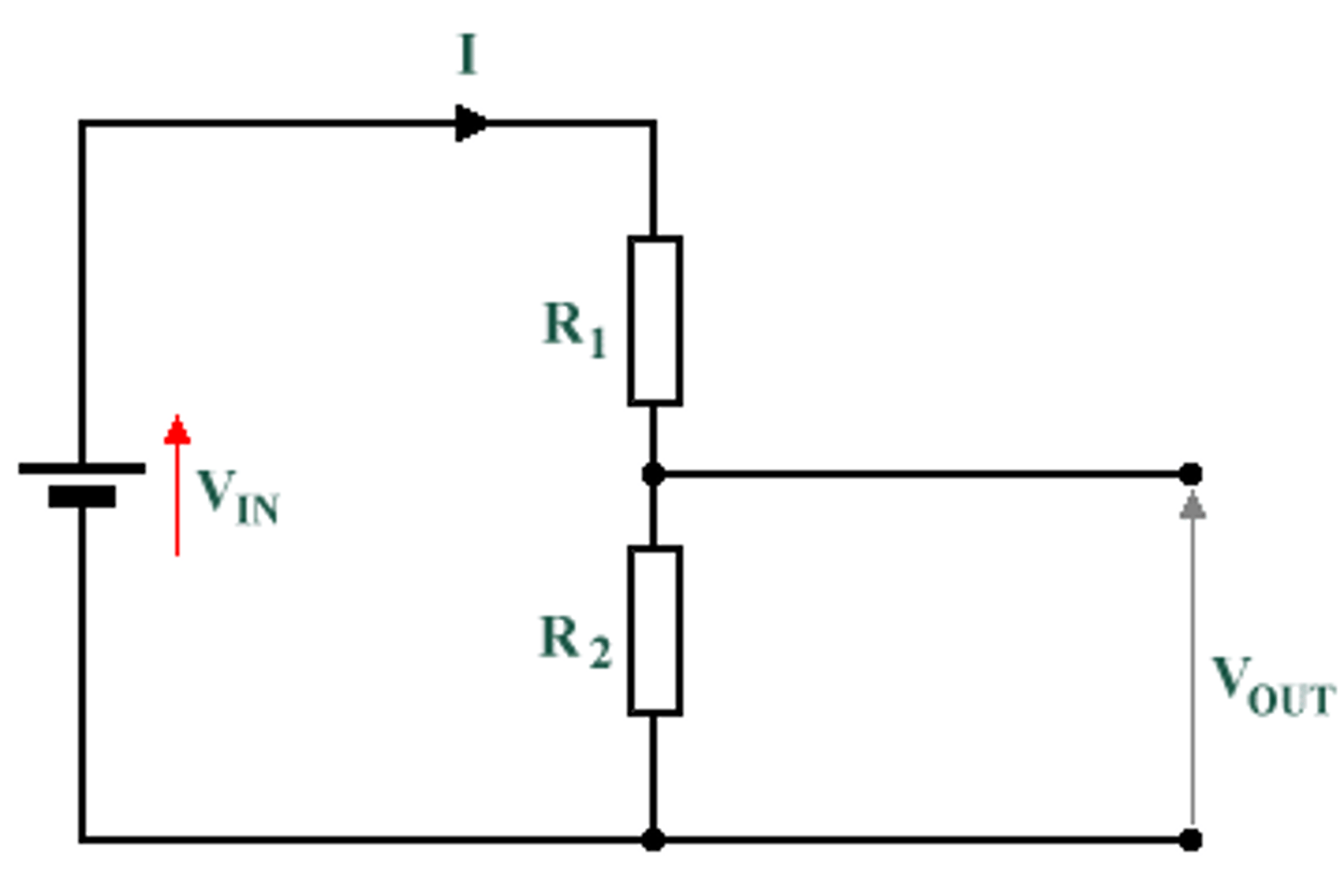
Potential divider (circuit with a voltage source and resistors in series)

V1 / V2 = R1 / R2

Intensity (W/m²)

Power / Area

Intensity

Intensity is the rate of flow of energy per unit area perpendicular to the direction of travel of the wave

Intensity is proportional to amplitude squared

Intensity ∝ Amplitude²

Polarised wave

Oscillates in one direction

Refractive index=

c / v

When a light ray passes across a boundary between two materials

n1 × sin θ1 = n2 × sin θ2

Refractive index of first / second material- n1 and n2

Angle of incidence / refraction- θ1 and θ2

Sin C=

1 / n

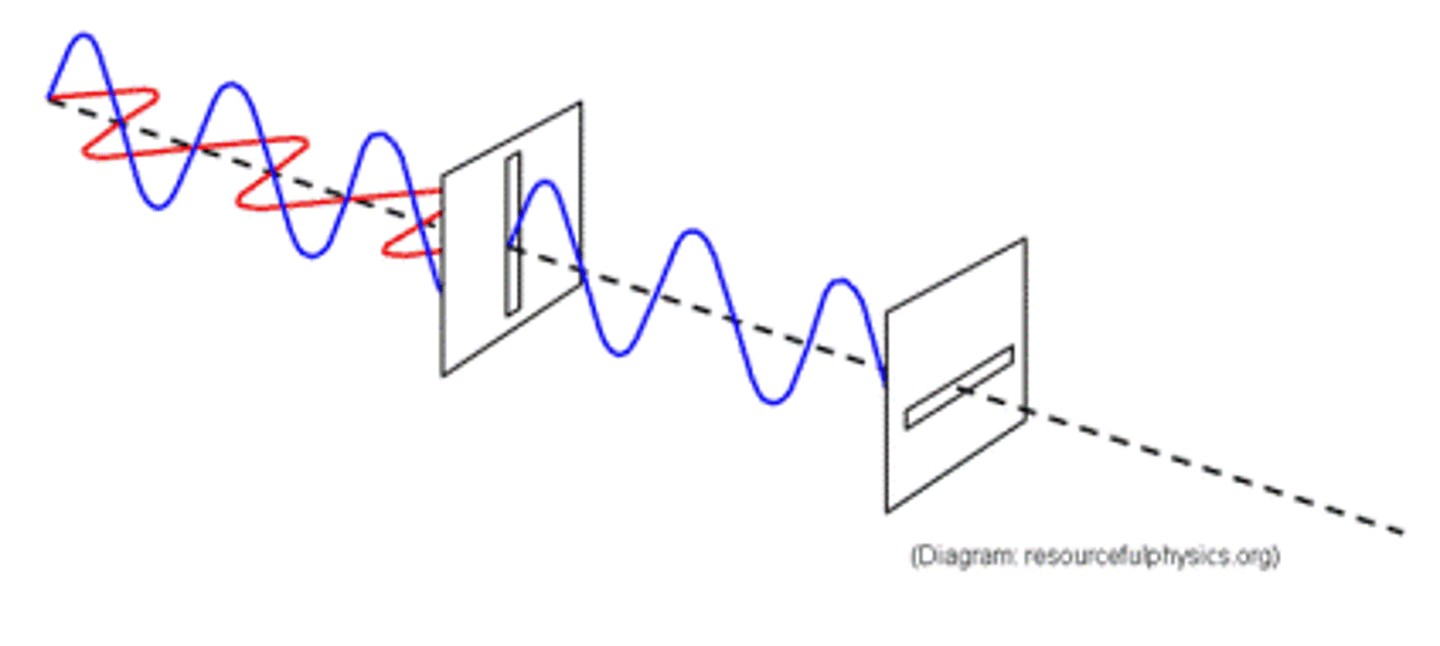
Coherent

Same wavelength and frequency with a fixed phase difference

Two coherent sources needed to get interference patterns

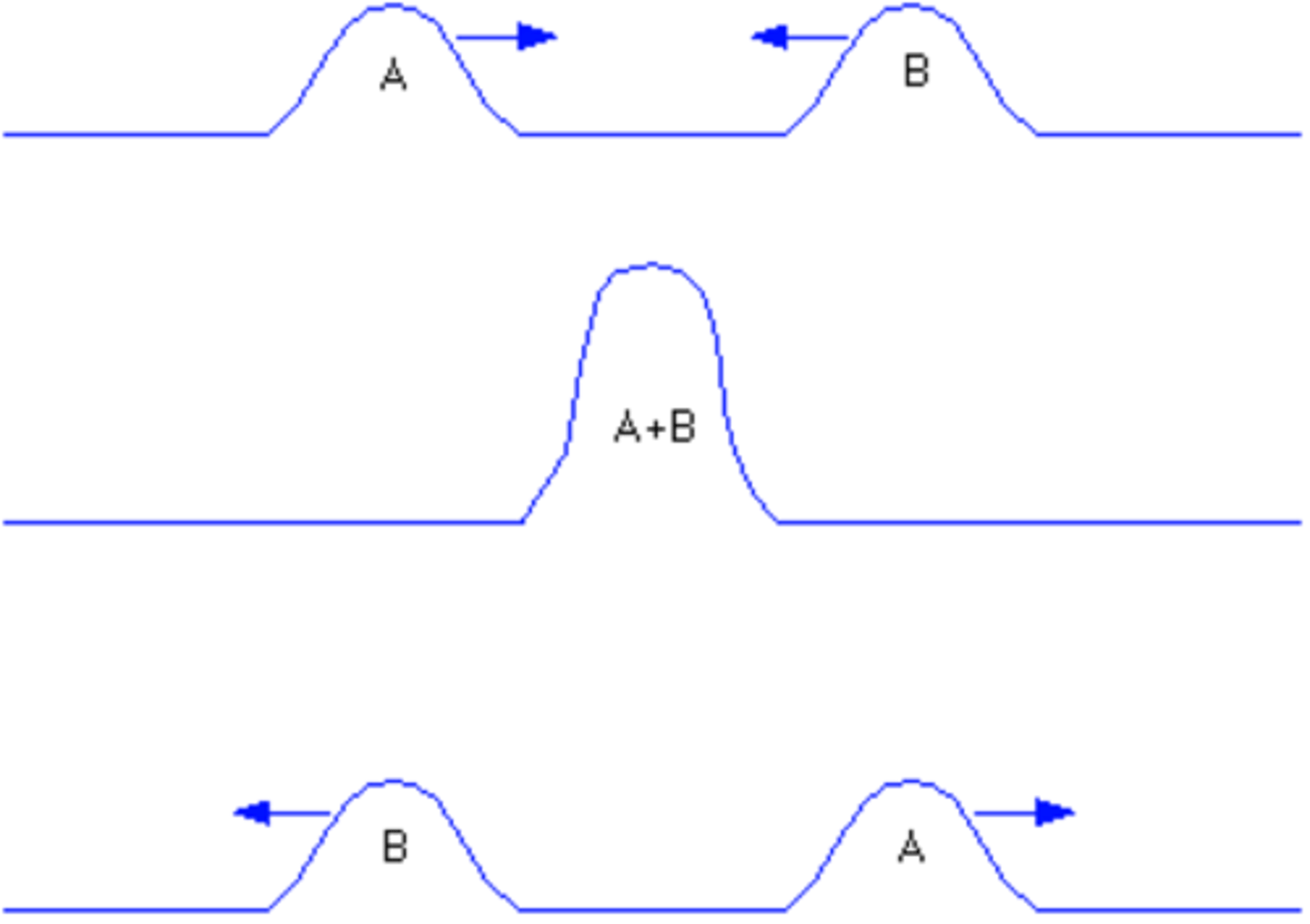
Constructive interference

Path difference is a whole number of wavelengths

Path difference = nλ

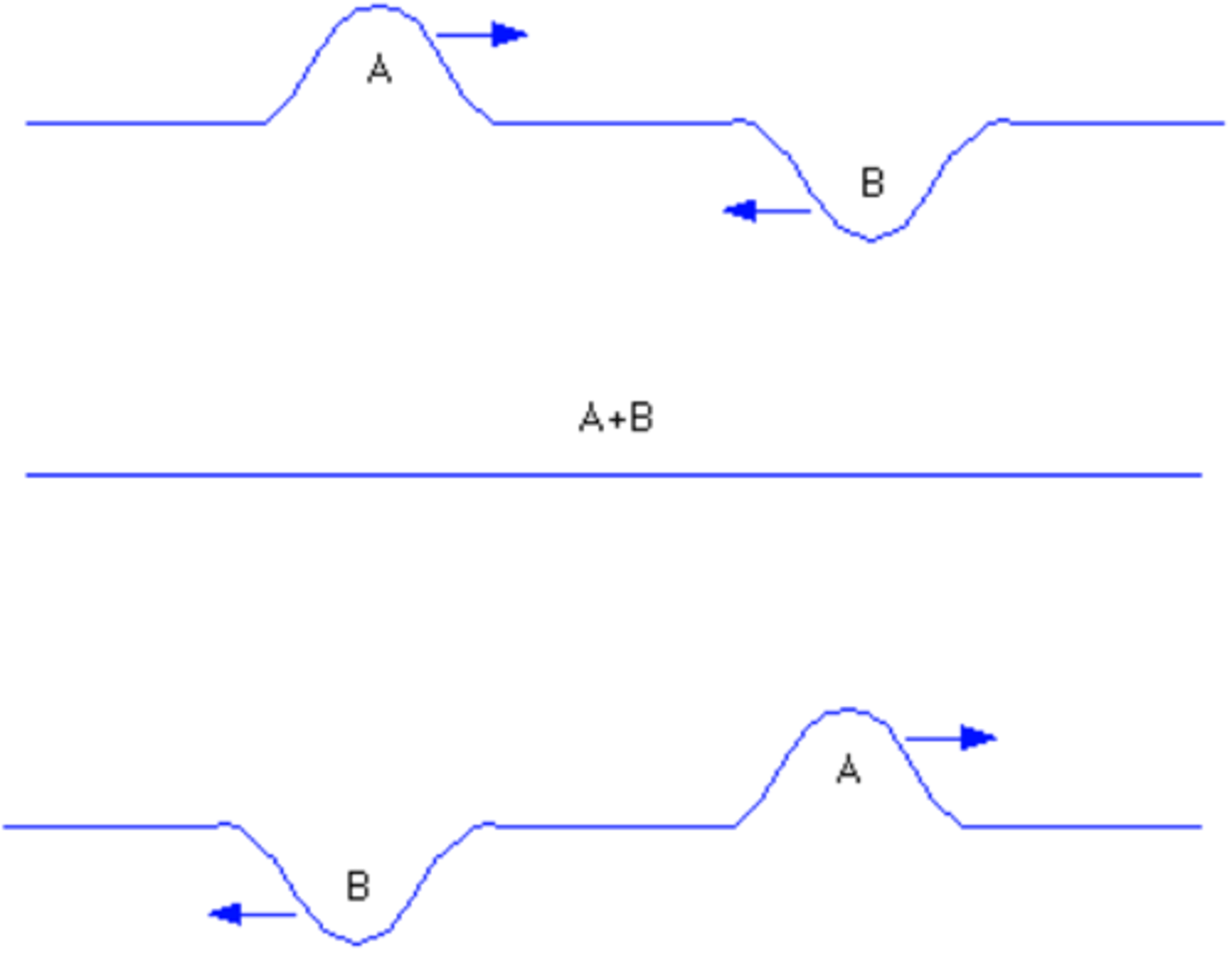
Destructive interference

Path difference is an odd number of half wavelengths

Path difference = (n + ½)λ

Fringe spacing, x=

λD / A

Stationary wave

The superposition of two progressive waves with the same wavelength, moving in opposite directions

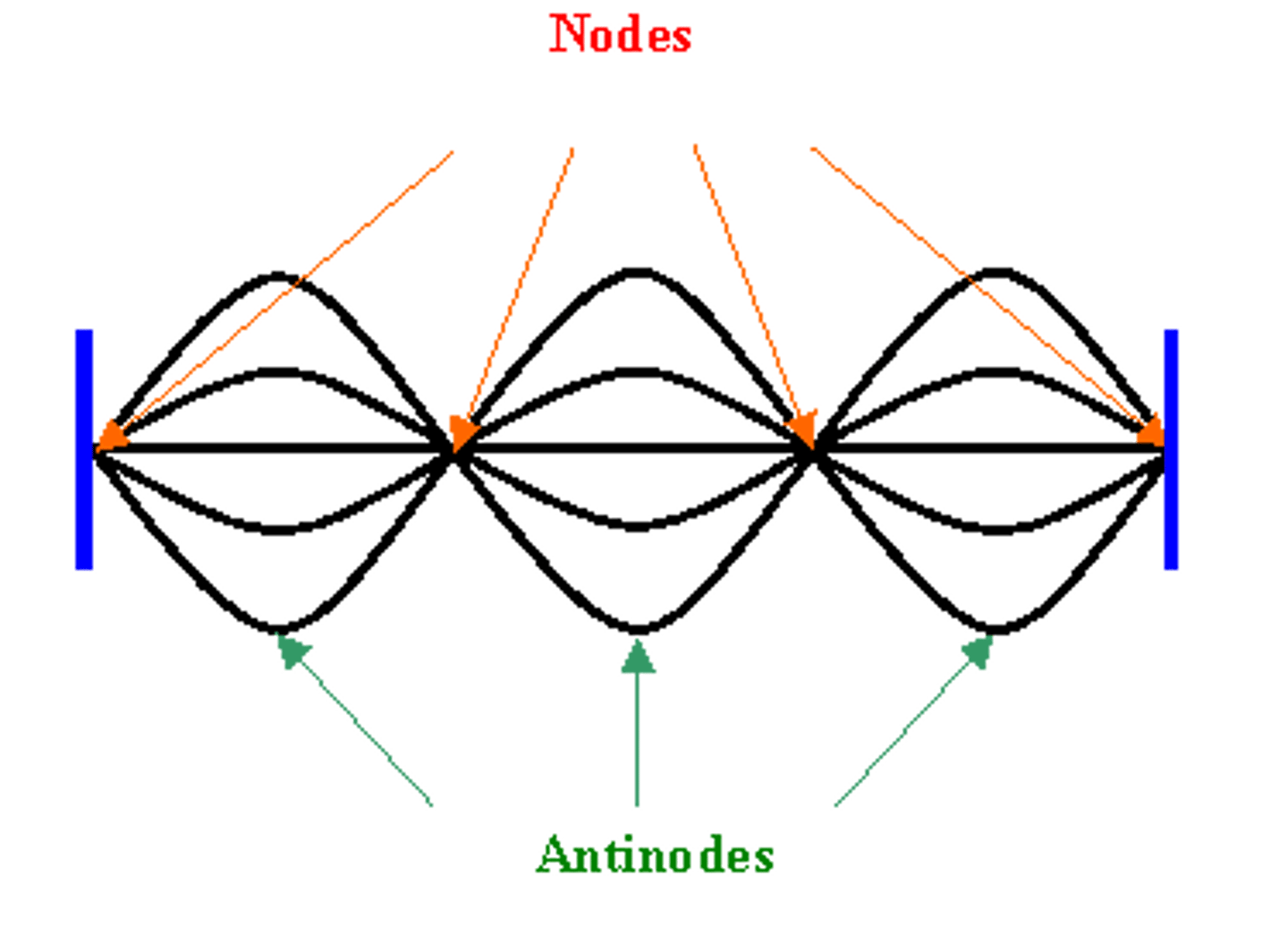
First harmonic

Second harmonic

Third harmonic

One antinode- half a wavelength

Two antinodes- one wavelength

Three antinodes- one and a half wavelengths

Photon

A quantum of EM radiation

E=

hf = hc / λ

Electronvolt

The kinetic energy gained by an electron when it is accelerated through a potential difference of one volt

1 eV = 1.6 × 10^-19 J

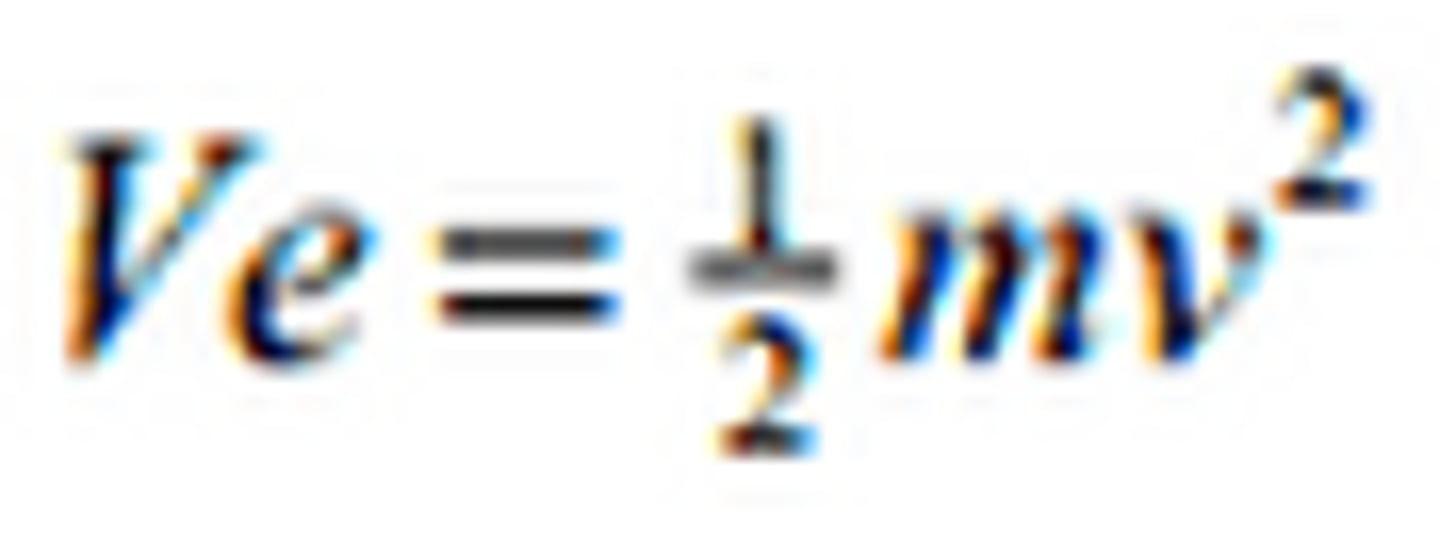
Photoelectric effect

1) No photoelectrons are emitted if the radiation has a frequency below a certain value (threshold frequency)

2) The photoelectrons are emitted with a variety of kinetic energies ranging from zero to some maximum value. The value of maximum kinetic energy increases with frequency and is unaffected by intensity

3) The number of photoelectrons emitted per second is proportional to intensity

Work function energy, Φ

Energy needed to break metallic bonds

Planck constant, h

6.63 × 10^-34 Js

Threshold frequency, f=

Φ / h

For electrons to be released

hf ≥ Φ

Maximum kinetic energy

hf=

Φ + max K.E.

de Broglie equation

λ=

h / p (momentum)

λ for electrons accelerated in a vacuum tube

Same size as electromagnetic waves in the X-ray part of the spectrum

Archimedes' principle

Upthrust = weight of fluid displaced