Modelling with Algorithms

What is a recursive algorithm?

It repeats instructions on a previous value stored. The instructions used will define the algorithm's output.

What is a graph?

A visual display of data, consisting of a finite set of vertices connected by edges

What is an edge?

An edge joins one vertex to another or starts and ends at the same vertex (a loop)

What are continuous graphs?

They have an infinite set of possible points on the plane and an infinite number of points on any curve or line you draw (e.g. x,y)

What is an algorithm?

A set of precise instructions which, if followed, will solve a problem

What is a heuristic algorithm?

It solves the problem but doesn't necessarily give the optimum solution

What is the efficiency of an algorithm?

A measure of the speed or time of operation of the algorithm

What is the worst case scenario for the bubble sort algorithm?

Reverse order O(n²)

What is the worst case scenario for the quick sort algorithm?

Correct or reverse order

How do you work out the number of comparisons to sort 'n' items in the worst case scenario for bubble sort and quick sort algorithms?

1/2n(n-1)

What are discrete sets of data?

Integers that can be counted and have a finite number of values

What are continuous sets of data?

Includes complex numbers and varying data values measured over a particular time interval

What is a simple graph?

One in which there are no loops and no multiple edges

What is a disconnected graph?

It falls apart into separate pieces

What is a connected graph?

Every vertex is linked by a single edge or sequence of edges to every other vertex

What is a complete graph?

A simple graph in which every vertex is connected to every other by a single edge

What is a complete graph with n vertices denoted by?

Kn

What is the degree of a vertex?

The number of edges which start and finish at it. A loop counts twice towards the degree as you start and finish at it. Only defined for a graph, not a digraph

What is the handshaking theorem?

If you find the sum of the degrees of the vertices in the graph and compare it with the number of edges, the sum of degrees of the vertices is twice the number of edges

What can the handshaking theorem be written as?

Σdegrees of vertices = 2 x edges

What are directed edges?

Edges that have a direction associated with them

What is a digraph?

A graph that has directed edges

What is a subgraph?

Part of a graph which is itself a graph

What is a planar graph?

One that can be drawn without any edges crossing

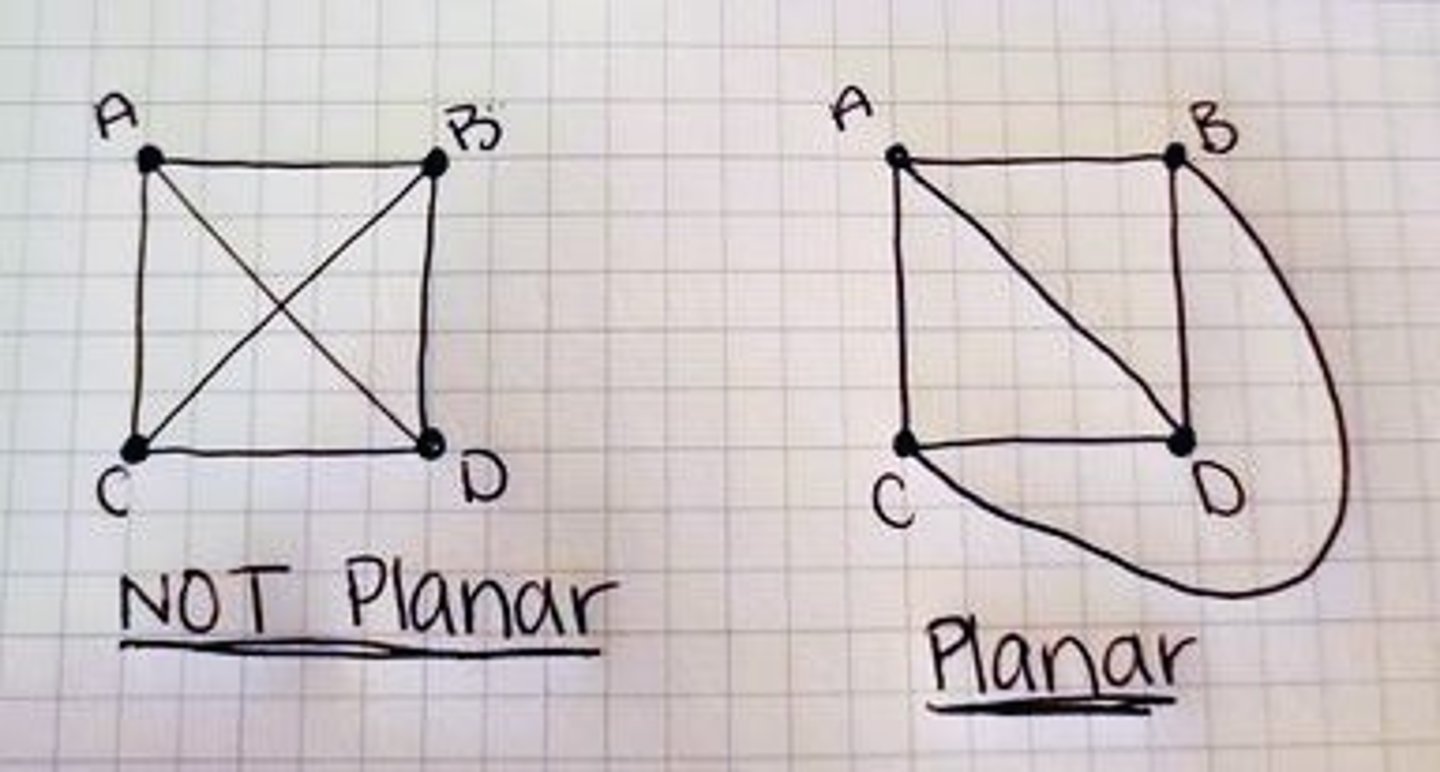
What is a bipartite graph?

Where there are two discrete sets of vertices with edges only joining vertices between sets and not within a set

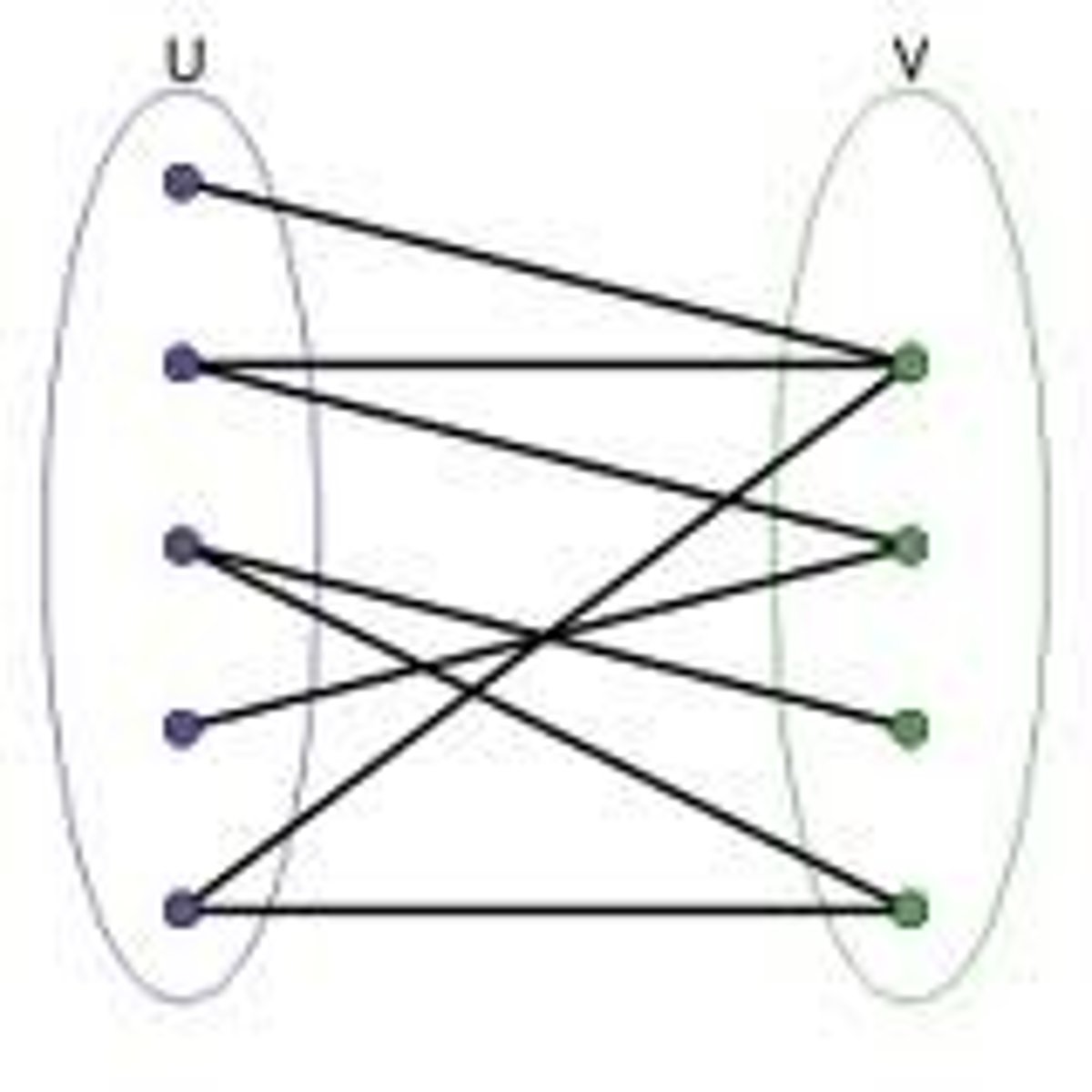
What is a complete bipartite graph?

Where each vertex in set A is joined to every vertex in set B by an edge

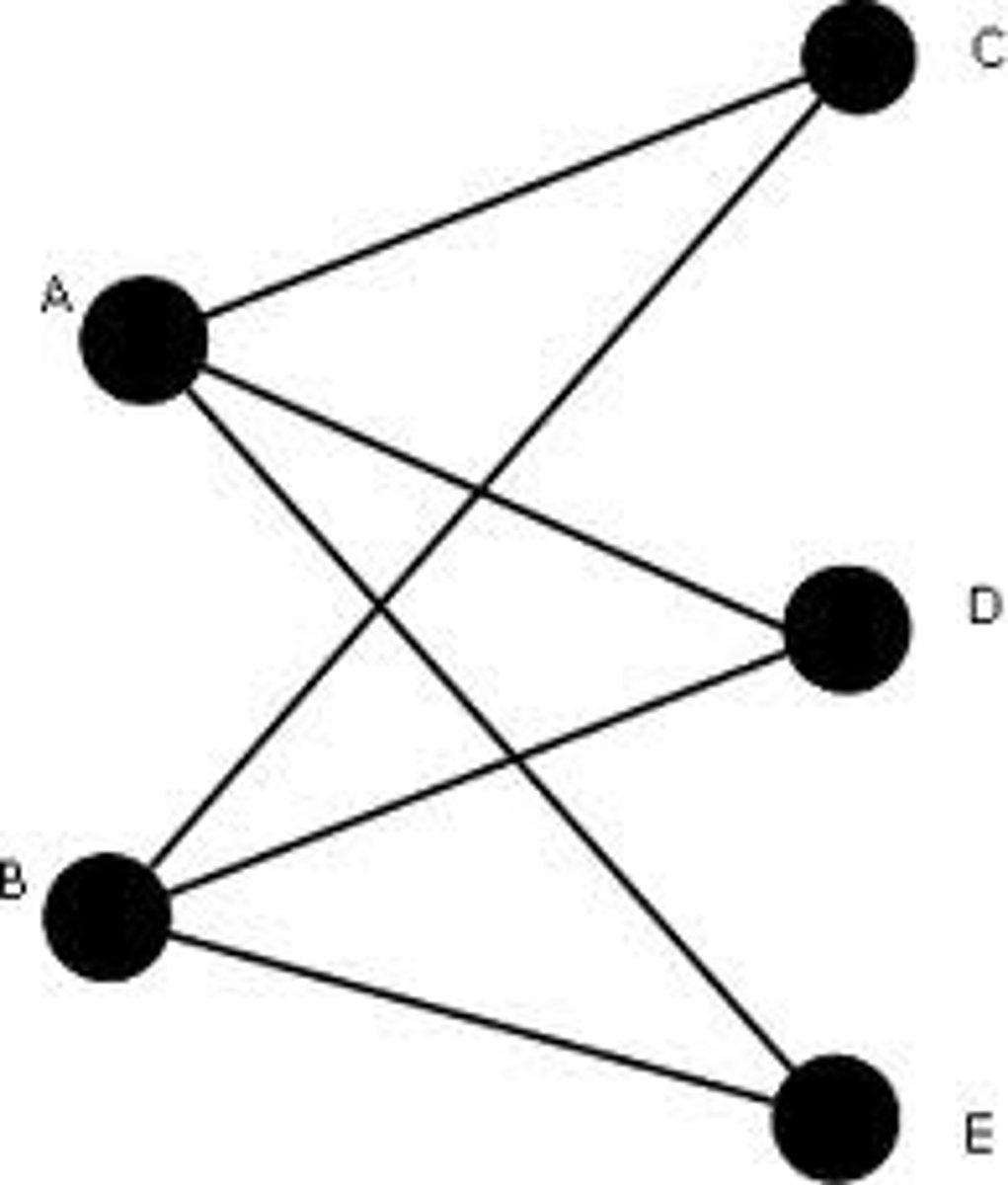
How can complete bipartite graph be denoted?

Kr,s (which would have a set of 'r' vertices joined to a set of 's' vertices)

What are isomorphic graphs?

Graphs with the same structure (including number of vertices and edges and degrees of the vertices) but drawn differently

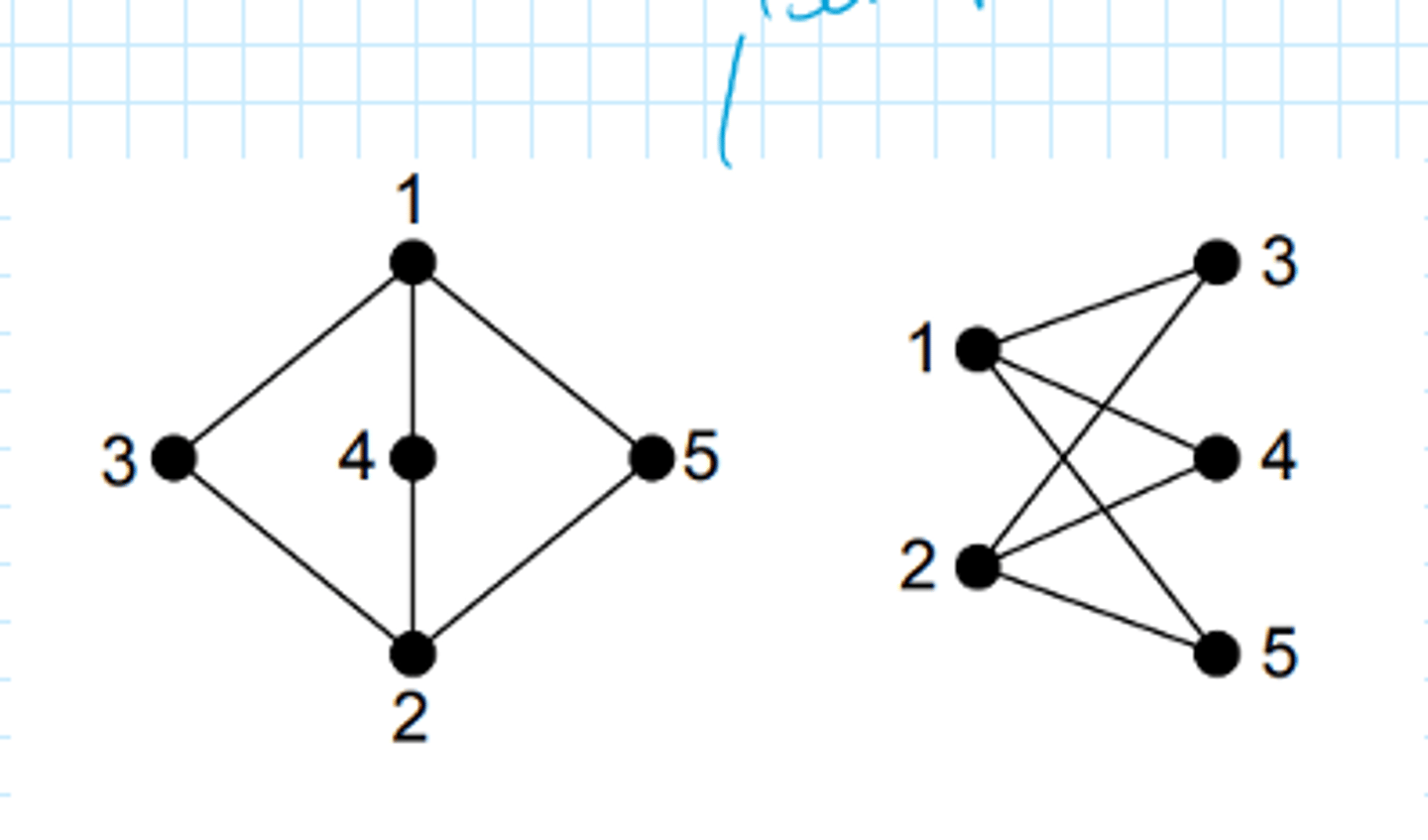
What is a tree?

A connected graph with no cycles

How can you check if a graph is a tree?

The number of edges is always one less than the number of vertices

What is a spanning tree?

A subgraph which includes all the vertices in the original graph and is also a tree

What is an incidence matrix?

Shows the number of edges from each point on a graph in the form of a matrix

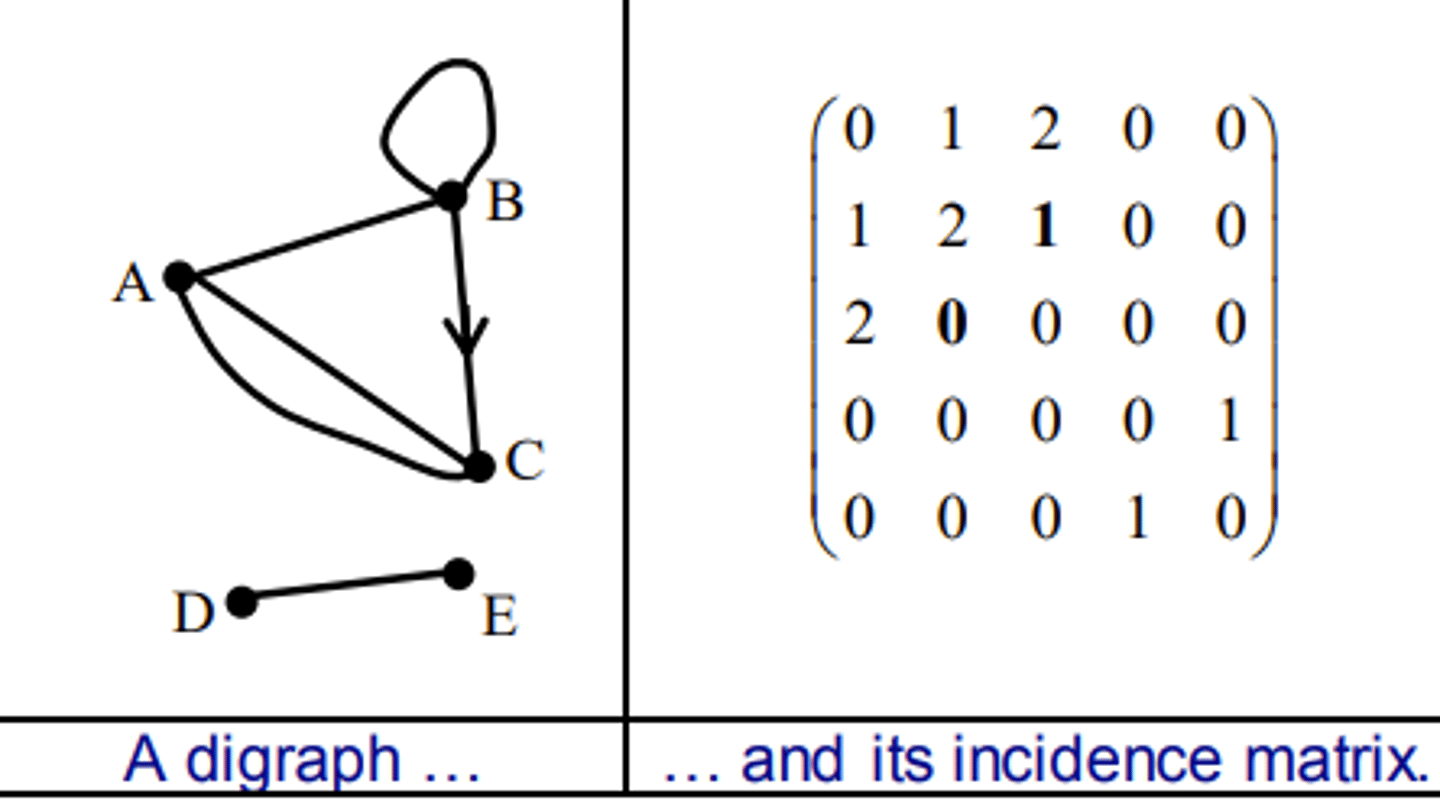
What does it mean if an incidence matrix has symmetry?

There are no directed edges

What is a weight?

The numerical value given to an edge

What is a network?

A graph with weighted edges

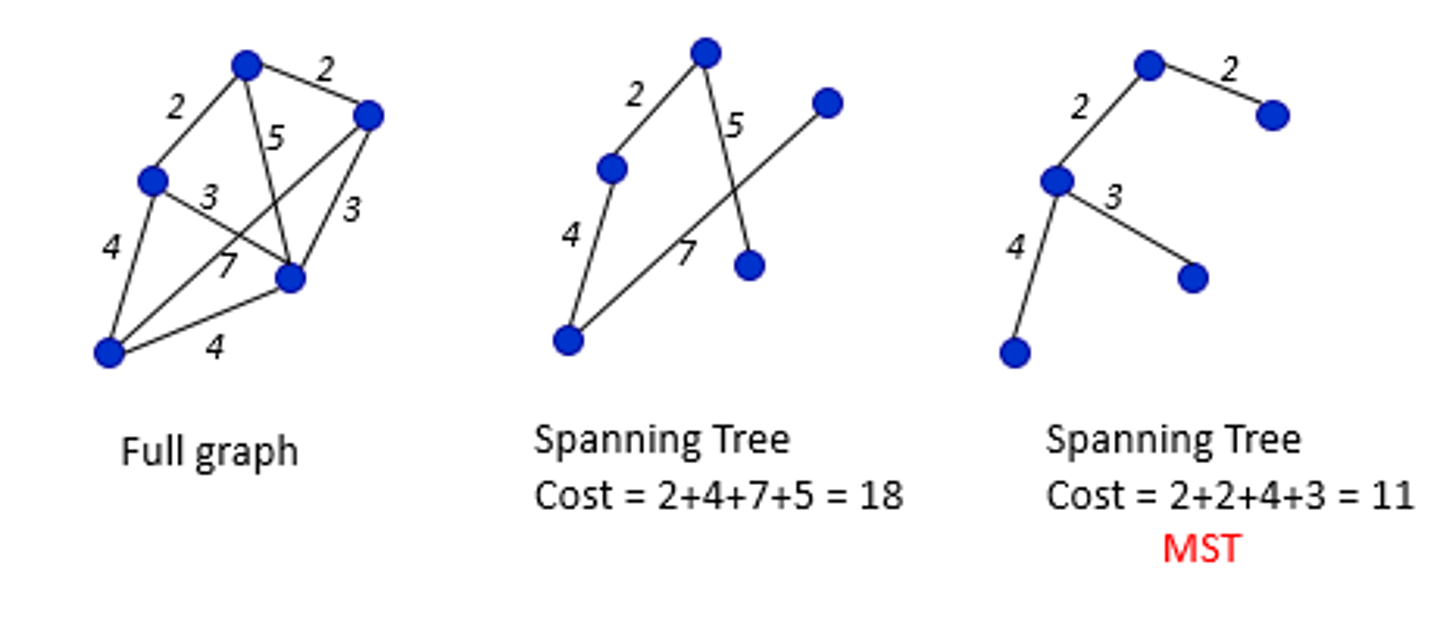
What is the Minimum Spanning Tree (MST)?

The set of edges which solves the minimum connector problem by connecting every vertex using the lowest weight. It is a subgraph with the same number of vertices as the original graph but also a tree

What is a greedy algorithm?

One which gives an optimal solution based on only one factor and doesn't consider other relevant factors

What is Kruskal's algorithm?

It builds a MST by listing the weights of the edges in ascending order and using the lowest weights to create a tree

How can you work out the length of the MST using the number of vertices?

For a network with 'n' vertices, the MST will have 'n-1' edges

What is Prim's algorithm?

It builds an MST by adding one vertex at a time

What is Dijkstra's algorithm?

It finds the shortest route through a network by assigning values to the vertices

What is the complexity for Kruskal's, Prim's and Dijkstra's algorithms?

O(n²)

What does the complexity of an algorithm represent?

The worst case scenario

What is complexity of the bubble sort algorithm when the list is already in order?

O(n)

What is the nth term for the total number of comparisons in the worst case scenario for first fit or first fit decreasing bin packing?

1/2n(n - 1)

How to calculate total float?

Late finish time - early start time - activity duration

How to calculate independent float?

Early finish time - late start time - activity duration (if result is -ve, say it = 0)

How to calculate interfering float?

Total float - independent float

What is it called when the flow through an arc is equal to its capacity?

It is saturated