Ch 7 - Sampling and Sampling Distributions

Element

Entity on which data are collected

Population

is a collection of all the elements of interest

Sample

The subset of the population

Sampled population

The population from which the sample is drawn

Frame

A list of the elements that the sample will be selected from

Why do we select samples?

• Answer research question about a population

• Sample results provide only estimates of the value of the population characteristics

• Sample contains only a portion of the population

• Proper sampling methods

  • The sample results can provide “good” estimates of the population characteristics

Selecting a Sample

• Sampling from a Finite Population

• Sampling form an Infinite population

Sampling from a Finite Population

Finite populations are often defined by lists such as:

• Organization membership roster

• Credit card account numbers

• Inventory product numbers

A simple random sample of size n from a finite population of size N is a sample selected such that each possible sample of size n has the same probability of being selected

Sampling w/ Replacement & Sampling w/out Replacement

1. Replacing each sampled element before selecting subsequent elements is called sampling with replacement. An element can appear in the sample more than once

2. Sampling without replacement is the procedure used most often

3. In large sampling projects, computer-generated random numbers are often used to automate the sample selection process

Sampling from an infinite

Sometimes we want to select a sample, but find that it is not possible to obtain a list of all elements in the population

• Cannot construct. frame for the population

• Hence we cannot use the random number selection procedure

• Most often this situation occurs in the case of infinite population

Sampling from an Infinite Population

• Populations are often generated by an ongoing process where there is no upper limit on the number of units that can be generated

• Some examples of on-going processes with infinite populations are:

  • Parts being manufactured on a production line

  • Transactions occurring at a bank

  • Telephone calls arriving at a technical help desk

  • Customers entering a store

Sampling from a finite Population

Sampling for an Infinite Population

Sampling from an Infinite Population

• Must select a random sample in order to make valid statistical inferences about the population from which the sample is taken

• A random sample from an infinite population is a sample selected such that the following conditions are satisfied

  • Each element selected comes from the population of interest.

  • Each element is selected independently

Point estimation

• A form of statistical inference

• We use the data from the sample to compute a value of a sample statistic that servs as an estimate of a population paramente

• We refer to x bar as the point estimator of the population mean

• s is the point estimator of the population standard deviation

• p hat is the point estimator of the population proportion p

p hat = x/n

sample

p = x/N

population

Target population

The poopulatin we want to make inferences about

Sample population

The population from which the sample is actually taken

• Whenever a sample is used to make inferences about a population, we should make sure that the targeted population and the sampled population are in close agreement

Sampling distributoin of x-bar

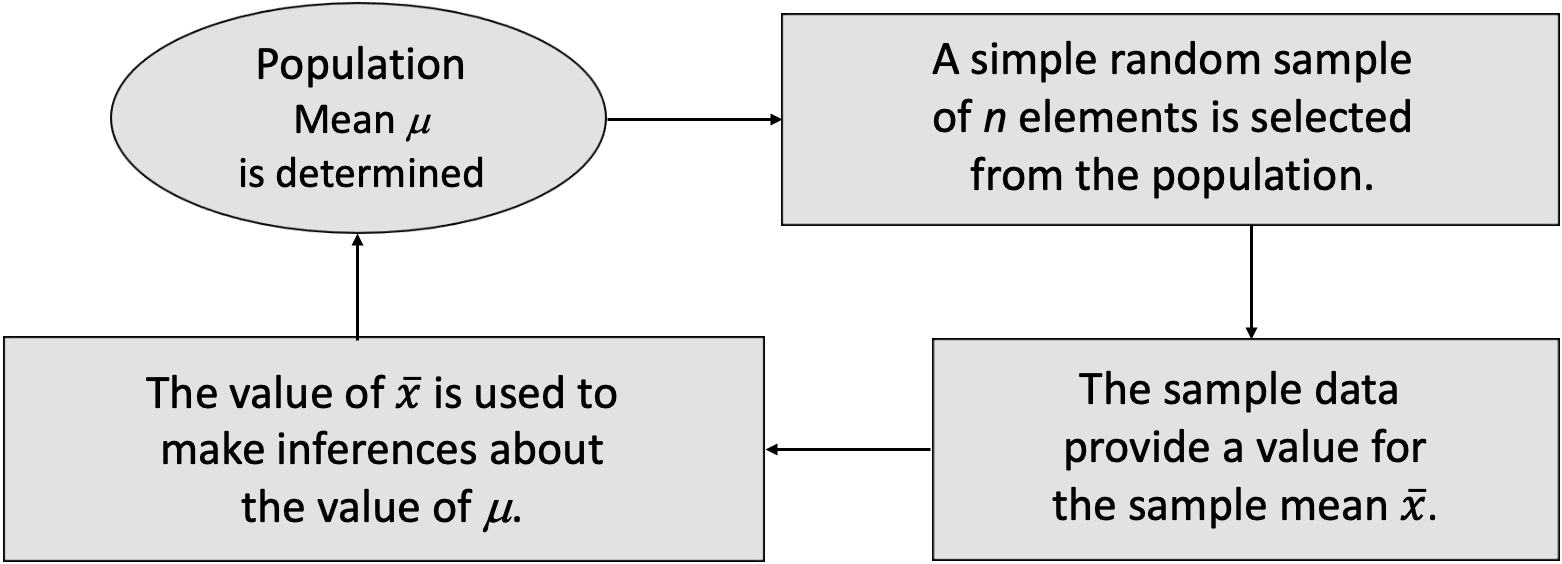
Sampling Distribution of x ̅   

•The sampling distribution of x ̅ is the probability distribution of all possible values of the sample mean x ̅.

•Expected Value of x ̅

•When the expected value of the point estimator equals the population parameter, we say the point estimator is unbiased.

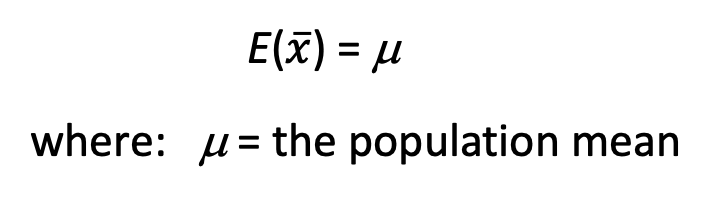
Sampling Distribution of x ̅   

•When the population has a normal distribution, the sampling distribution of x ̅ is normally distributed for any sample size.

•In most applications, the sampling distribution of x ̅ can be approximated by a normal distribution whenever the sample is size 30 or more.

In cases where the population is highly skewed or outliers are present, samples of size 50 may be needed

•The sampling distribution of x ̅ can be used to provide probability information about how close the sample mean x ̅ is to the population mean m .

Central Limit Theorem

•When the population from which we are selecting a random sample does not have a normal distribution, the central limit theorem is helpful in identifying the shape of the sampling distribution of x ̅.    

Relationship Between the Sample Size and the Distribution of X Bar

Example: St. Andrew’s College

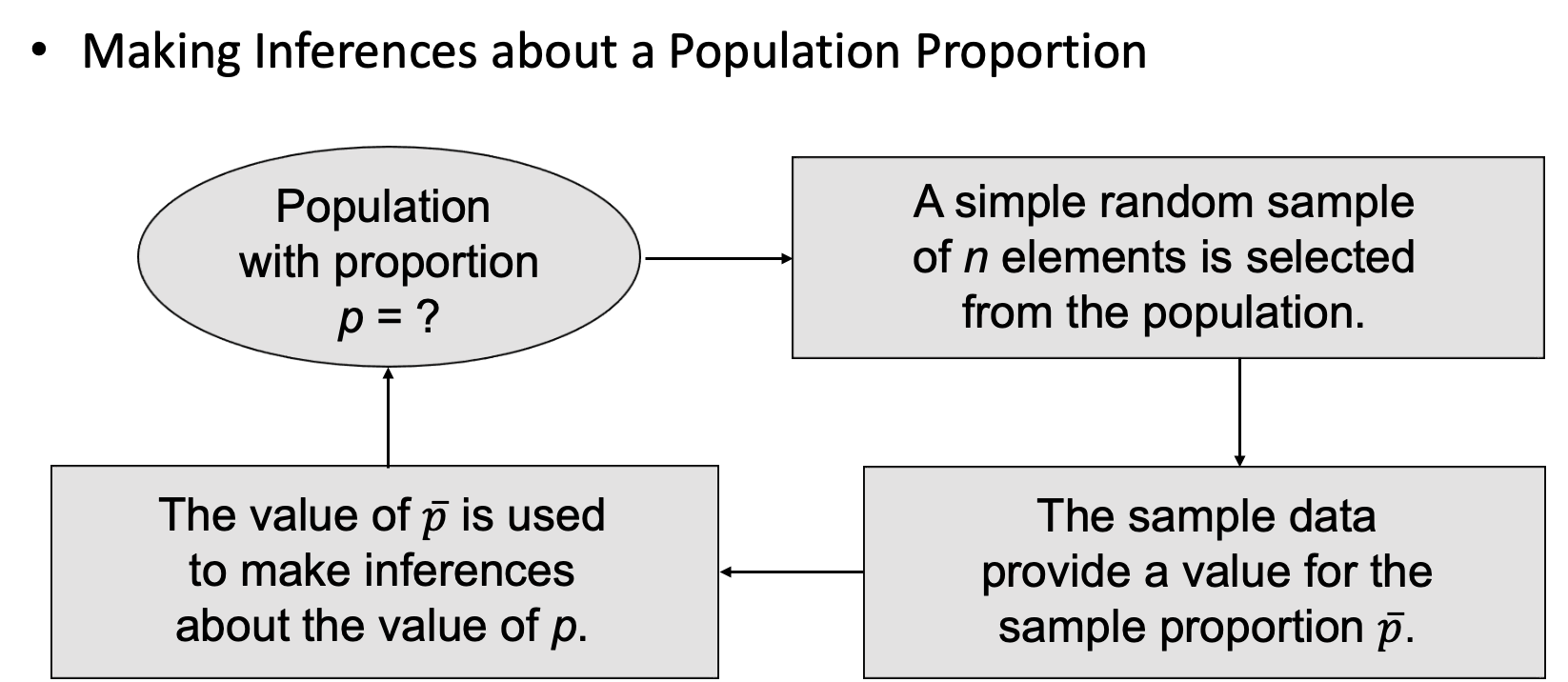
Sampling Distribution of P hat (Population proportion)

•The sampling distribution of p ̅  is the probability distribution of all possible values of the sample proportion p ̅.

Stratified Random Sampling

The population is first divided into groups of elements called strata

• Each element in the population belongs to one and only one stratum

• Best results are obtained when the elements within each straum are as much alike as possible (i.e. a homogenous group)

•A simple random sample is taken from each stratum.

•Formulas are available for combining the stratum sample results into one population parameter estimate.

•Advantage:  If strata are homogeneous, this method provides results that is as “precise” as simple random sampling but with a smaller total sample size.

Example:  The basis for forming the strata might be department, location, age, industry type, and so on

Cluster Sampling

•The population is first divided into separate groups of elements called clusters.

•Ideally, each cluster is a representative small-scale version of the population (i.e. heterogeneous group).

A simple random sample of the clusters is then taken

•All elements within each sampled (chosen) cluster form the sample.

•Example:   A primary application is area sampling, where clusters are city blocks or other well-defined areas.

•Advantage:  The close proximity of elements can be cost effective (i.e. many sample observations can be obtained in a short time).

Disadvantage:  This method generally requires a larger total sample size than simple or stratified random sampling

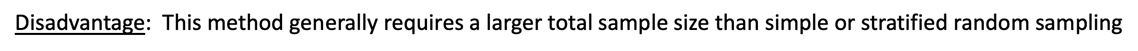
Systematic sampling

If a sample size of n is desired from a population containing N elements, we might sample one element for every N/n elements in the population

•We randomly select one of the first N/n elements from the population list.

•We then select every N/nth element that follows in the population list.

•This method has the properties of a simple random sample, especially if the list of the population elements is a random ordering.

•Advantage:  The sample usually will be easier to identify than it would be if simple random sampling were used.

•Example:  Selecting every 100^th listing in a telephone book after the first randomly selected listing.

Convenience Sampling

It is a nonprobability sampling technique.  Items are included in the sample without known probabilities of being selected

The sample is identified primarily by convenience

Example:  A professor conducting research might use student volunteers to constitute a sample

Advantage:  Sample selection and data collection are relatively easy

•Disadvantage:  It is impossible to determine how representative of the population the sample is.

Judgement Sampling

•The person most knowledgeable on the subject of the study selects elements of the population that he or she feels are most representative of the population.

•It is a nonprobability sampling technique.

•Example:  A reporter might sample three or four senators, judging them as reflecting the general opinion of the senate.

Advantage:  It is a relatively easy way of selecting a sample

Disadvantage:  The quality of the sample results depends on the judgment of the person selecting the sample

Recommendation