Kin 483-Ch.7 Correlation and Prediction

Exam 2

Correlation (definition)

Numerical coefficient that indicates the relationship between 2 variables

Attributes of r

• demonstrates a linear relationship

• positive relationship

• negative relationship

• always between -1.0 and 1

• value of 0 = no relationship

• (±)0.3: low

• (±)0.7: high

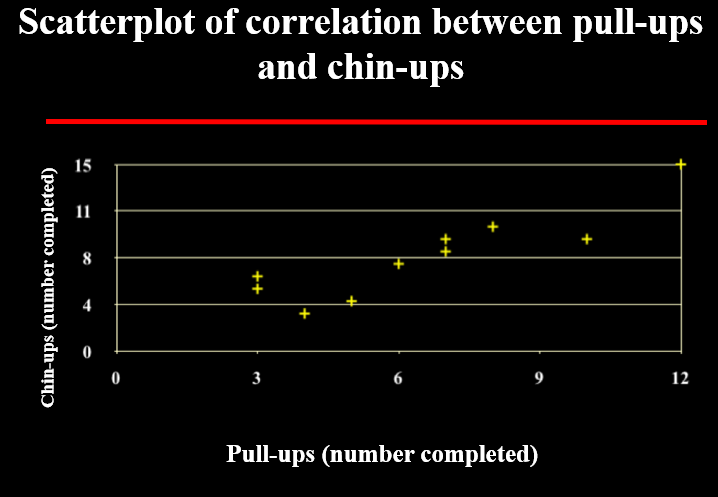
Positive relationship

• as one variable increases, the other variable also increases (and vise versa)

• direct relationship

  • ex: leg press and bench press weights both increase

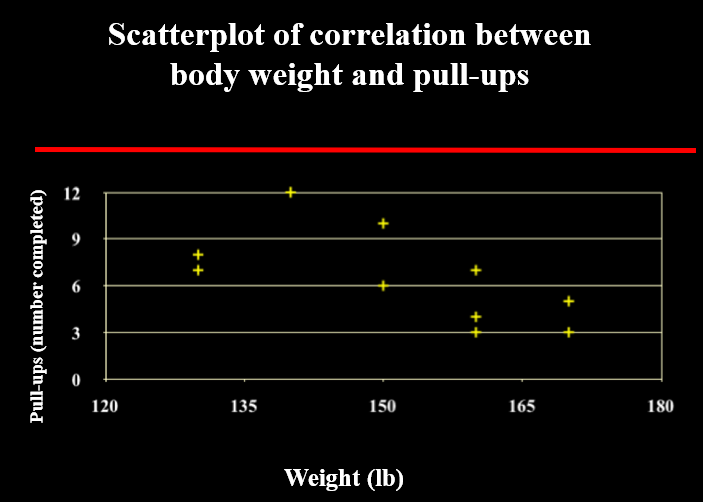
Negative relationship

• as one variable increases, the other variable decreases (and vise versa)

• indirect relationship

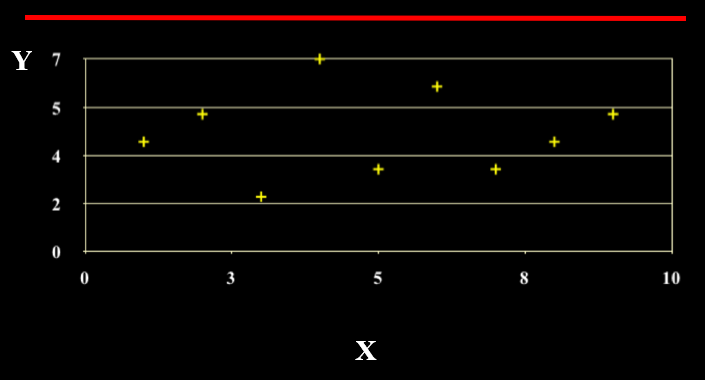
Scatterplot of zero correlation (r=0)

Correlation formula

SPSS and Correlation (Steps)

1. File —> Open —> Data (select data)

2. Analyze —> Correlate —> Bivariate

3. Choose variables you want to correlate

4. Correlation table formed!

Note:

• strong correlation: >0.7

• Significant two tail = p-value: statistical difference; accepted alpha in kinesiology is 0.05

• Strong relationship is statistically significant

SPSS and Scatterplot (Steps)

1. Insert data

2. Graphs —> Scatter

3. Simple

4. Define

5. Put variable 1 (ex: body weight) in the x-axis box

6. Put variable 2 (ex: chin ups) in the y-axis box

7. click ok

Coefficient of Determination

Represents the proportion of shared variance between the 2 measures in question (r²)

Example:

• Correlation between a distance run and VO2 max is r=0.9 (strong positive/direct relationship)

• r² = 0.81, percentage of shared variance betw. 2 variables is 81%

• performance in the distance run accounts for 81% of variation in VO2 max values

• 19% of the variance is unique variance in VO2 max that cannot be explained by the run test (error/residual variance)

Correlation issues

CORRELATION DOES NOT = CAUSATION!!!!

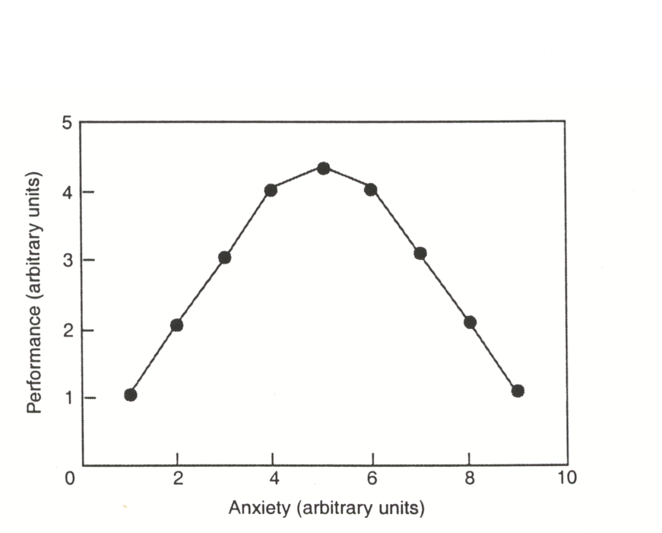
Limitations of r: Curvilinear or Linear

• in this case, the Pearson Product Moment correlation would give an r close to zero (no relationship)

• but isn’t there a relationship? this is where scatter plots come in

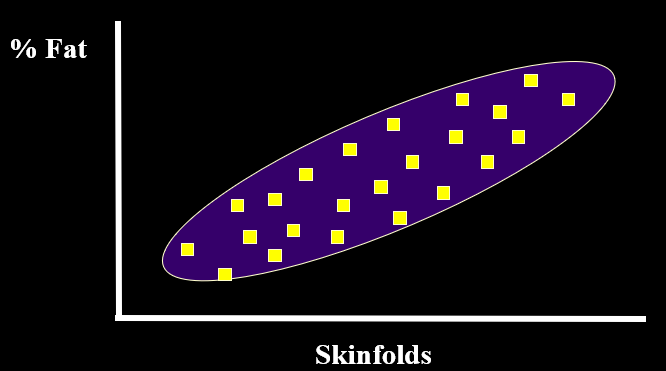
Correlation and Prediction

• illustrates the positive correlation between skinfold thickness and percent fat

• predict body fat % based on skin fold

Linear Regression (definition)

• We can make predictions using Simple Linear Regression

  • An outcome variable (dependent variable can be predicted from a single predictor aka independent variable)

  • If both the dependent and independent variables are correlated we can compute a prediction equation

SPSS and Linear Regression (steps)

1. Import data

2. Analyze —> Regression —> Linear

3. Assign dependent and independent variables

4. Ok

Note:

• First box: r value and r²

• Second box: regression, degrees of freedom, SIG (p-value)

• Third box: values to plug into y=mx+b

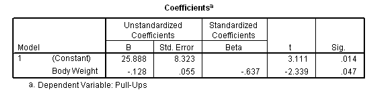
Prediction Formula

Y’=bX + c

Example: Predicted pull ups (Y’)=-0.128 * body weight (lbs) +25.88

Multiple Regression/Correlation

• a single dependent variable (Y)

• multiple independent variables

• Y’=m1X1 + m2X2 +m3X3 + …b

• an extension of simple correlation

3 Types of Multiple Regression

• Standard Multiple Regression: 1 equation with all independent variables included

• Hierarchical Multiple Regression: We override the computer and set up a hierarchical order for inclusion in variables; useful if some IV’s are easier to measure than others

• Stepwise Multiple Regression: computer provides multiple equations with different combinations of IV’s