Ch 16: Indexing

Indexing

• data structure technique to optimize the performance of a database by minimizing the number of disk accesses required when query is processed

• Basic algorithm to search – linear. However, complex search queries (especially with joins) impacts performance

• helps improve performance

Remember to create indices to match expected query workload

The key for the index

can be any attribute or set of attributes and  need not be the key for the relation on which the index is built.

Rule of thumb for indexing

Create an index on the attribute that is used frequently in the search

Index

a pointer to data in the table (takes a value for some field(s) and finds records with the  matching value quickly) has components search key and data reference.

Search Key

Field(s) on whose values the index is based

May be primary key or candidate key of the table (sorted order)

Data Reference

Holds the address of the disk block(or row) where the key value can be found

Access types(Aspects)

• Finding records with a specified attribute value (search key), or

• Finding records with attribute value based on a specified range

Access Time(Aspects)

•Time needed to find a particular data item or set of data items

Insertion Time(Aspects)

•Time to find the place to insert + time to insert a new data item + time to update the index structure

Deletion Time(Aspects)

•Time to find the data item to be deleted + time to delete the data + time to update the index structure

Space Overhead(Aspects)

•Space occupied by an index structure (vs. performance)

Sequential file organization (or Ordered index) (File Org Mechanism)

• Indices based on sorted ordering of the values

• Generally fast

• Basic / traditional structure that most DBs use

Hash file organization (or Hash index) (File Org Mechanism)

• Indices based on a uniform distribution of values across a range of buckets

• Hash function determines a value assigned to a bucket

Primary index (or clustered index)

• Search key defines the sequential order of the file

• Search key of a clustering index is often the primary key (but not necessarily so)

Secondary index (or unclustered index)

• Search key specifies an order different from the sequential order of the file

• Use an extra-level of indirection to implement a secondary index, containing pointers to all the records

Ordered Index

• Data structure created on the basis of the key of the table

• Ordered file with fixed, two fields(search key and data reference)

Unique to each record (i.e., 1:1 mapping)

Since primary keys are stored in sorted order, the performance of the search operation is quite efficient

Two types:

• Dense index

• Sparse index

Dense Index

• A record is created for every search key value

• Need more space to store index records

• Example: a search key is a primary key

• Support range queries

• Pointer points to the first data record with the search-value.

• The rest of the records are sorted on the same search key

• Primarily uses linear search

Dense Index Lookup

Given a search key K, the index is scanned:

• When K is found, the associated pointer to the data file recorded is followed and the block containing the record is read in main memory

When dense indexes are used for non-primary key, the minimum value is located first

• Consecutive blocks are loaded in main memory until a search key greater than the maximum value is found

The index is usually kept in main memory. Thus one disk I/O has to be performed during lookup

Since the index is sorted, a binary search can be used.

• If there are n search keys, at most log2n steps are required to locate a given search key

Query-answering using dense indices is efficient

Sparse Index

• Used when dense indices are too large

• One key-pointer pair per data block

• Can be used only if the relation is stored in sorted order of the search key

• Start with search-key value less than or equal to the desired search value, then linear search

• Primarily uses binary search

Differences between Dense vs Sparse Indexes

A primary index that is dense on an ordered table is redundant

Thus, a primary index on an ordered table is always sparse

• Dense indices are faster in general

• Sparse indices require less space and impose less maintenance for insertions and deletions

Try to have a sparse index with one entry per block

(Try to keep index size small)

Multi-level Indices

If an index is small enough to be kept entirely in main memory, the search time to find an entry is low

If index is too large to be kept in main memory, index blocks

must be fetched from disk when required. One search results in several disk-block reads

If no overflow blocks in the index → use binary search

If overflow blocks → use sequential search

Solution:

Use a sparse index on the index

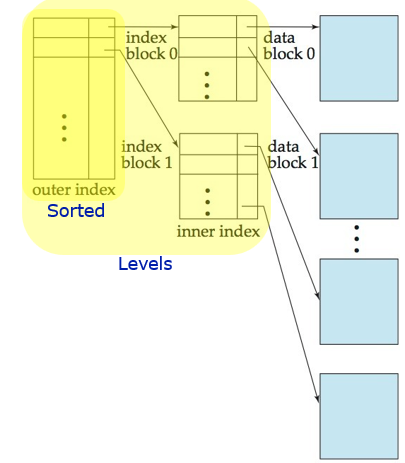
Two-Level Sparse Index

• Use binary search on outer index

• Scan index block until the correct record is found

• Scan block pointed to for desired record

• For very large files, add additional level of indexing to improve search performance

• Must update indices at all levels when perform insertion or deletion

Updating Indices(Insertion)

Find a place to insert

For dense index:

• Insert search key value if not present

For sparse index:

• No change unless a new block is created

• If the first search key value appears in the new block, insert the search key value into the index

Updating Indices(Deletion)

Find the record

If it is the last record, delete that search key value from index

For dense index:

• Delete the search key value

For sparse index:

• Delete the search key value

• Replace the key value’s entry index with the next search key value if not already present

Implementation of Update/Delete using B+ Trees

Reorganization(update/delete) is costly, so:

B+ Tree

• A tree-like file structure

• Links nodes with pointers

• Has exactly one root, bounded by leaves

• Has unique path from root to each leaf; all paths are equal length

• Store keys only at leaves, references in other/internal nodes

• Guides key search via the reference values, from root to leaves

• Balance – same length on every path from root to leaves

• Extensible – number of pointers (n) at any given node

B+ Tree Nodes

root, internal, or leaf nodes.

Each node is exactly one disk page (“page” and “node” are used interchangeably)

Contain n pointers and (n - 1) key values

Low n vs High n

Small value for n -- Tall and thin B+ tree

• Advantage: Good consistent performance

• Equal depth of tree → constant lookup time

• Disadvantage: High overhead when insert/delete

• Need to reorganize up and down the tree

Large value for n -- Short and wide B+ tree

• Advantage: Low overhead

• Disadvantage: Performance varies

Index-Sequential Files

Disadvantage:

• Performance degrades as sequential file grows because many overflow blocks are created

• Periodic reorganization of entire file is required

B+ Tree Index File

Advantage:

• Automatically recognize itself with small, local changes (when insert or delete data)

• Range queries on indexed attributes are fast

Disadvantage:

• Extra insertion deletion overhead, space overhead

B+ Tree indices are alternatives to index sequential files

B+ Trees are used extensively in all DBMS

Cost of Disk I/O Operations(w/o an index/full sequential scan)

Without an index, need sequential scanning

Estimated cost = # blocks scanned

Cost of I/O Operations(primary/clustered index)

Use clustered index, index and data are sorted the same way

Estimated cost = selectivity estimate x #blocks

Cost of I/O Operations(secondary/unclustered index)

Use unclustered index, index and data are sorted differently

Estimated cost = selectivity estimate x #tuples

Worse case: read a  different block every  time. Thus, choose  key(s) carefully

Using an unclustered index  in the wrong scenario can  lead to low performance. What could work better possibly?

Full sequential scan is a better option when

•Selectivity is high (many tuples match the selection), or

•Ratio between #tuples:#blocks is high(Ex: 10000 tuples and 100 blocks,

10000/100 is big, so the ratio is high.

Read-heavy DBs

can index a lot (if space allows)

Write-heavy DBs

index sparingly (take a balanced approach)  

Write-only DBs

one or no index