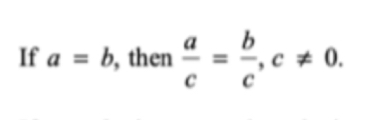Honors Geometry Vocabulary

Symmetry

a geometric characteristic of both nature and art.

Reflectional symetry

a design has reflectional symmetry if you can fold it along a line of symmetry so that all the points on one side of the line exactly coincide with all the points on the other side of the line.

Rotational symmetry

A design has rotational symmetry if it can be rotated around a central point by a certain angle and appear unchanged.

bilateral symmetry

an object with only one line of symmetry.

Segment

A part of a line that is bounded by two distinct endpoints.

Ray

A ray is bound by an endpoint on one side and extends infinitely in the other direction.

Oposite rays

Two collinear rays that extend infinitely oposite directions along a line.

Intersection

2 or mere geometric figures intersect when they have one or more points in common.

Ruler postulate

the points on a line can be matched one to one with real numbers. The real number that corresponds to a point is the coordinate of the point. The distance between points A and B, written as AB, is the absolute value of the difference of the coordinates of A and B.

Construction

a construction is a geometric drawing that uses a limited set of tools, usually a compass and a straightedge.

Congruent segments

line segments that have the same length are called congruent segments.

Segment addition postulate

when three points are collinear, you can say that one point is between the other two.

Segment addition postulate formula

AC = AB + BC

Polygon

a closed plane figure formed by three or more line segments called sides b

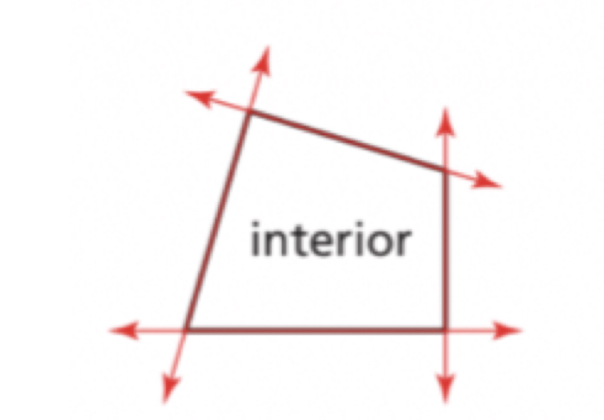
Convex polygon

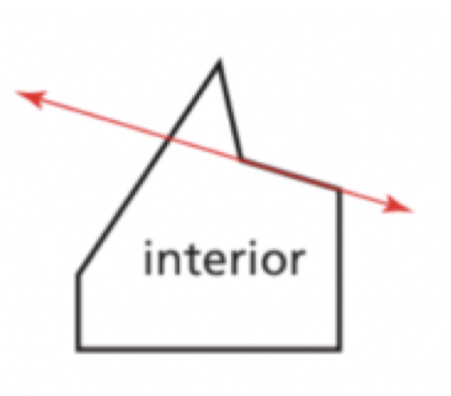
Concave polygon

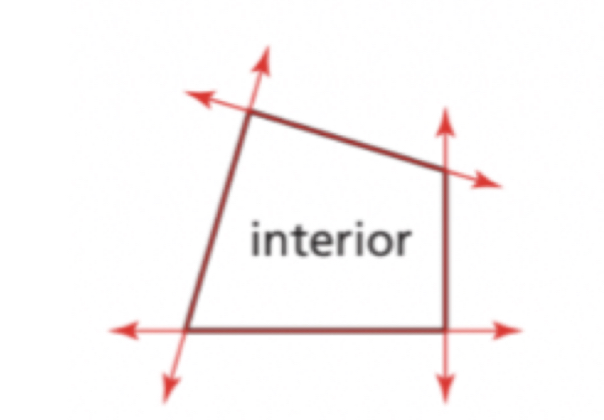
Convex

a polygon is convex when no line that contains a side of the polygon contains a point in the interior of the polygon.

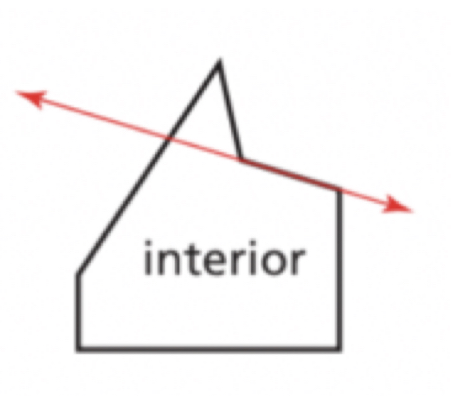
Concave

A polygon is concave when one or more line that contains a side of the polygon contains a point in the interior of the polygon.

Radical expression

an expresion that contains a radical.

Rationalizing the denominator

When a radical is in the denominator of a fraction, you can multiply the fraction by an appropriate form of 1 to eliminate the radical from the denominator.

Conjugates

are used to simplify radical expressions that contain a sum or difference involving square roots or radicals in the denominator.

Like radicals

radicals with the same index and radicand. These can be added and subtracted the same way like terms are combined by using the Distribution Property.

Midpoints

a point that decides the segment into 2 congruent segments

Segment bisector

A point, line, line segment, or plane that intersects the segment at its midpoint.

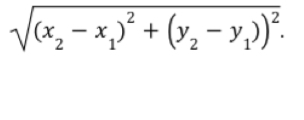
Distance formula

Midpoint Formula

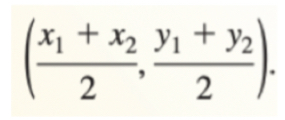
Angle

A set of points consisting of two different rays that have the same endpoint, called a vertex. The rays are the sides.

Interior of the angle

The region that contains all the points between the sides of the angle.

Exterior of the angle

The region that contains all the points outside the sides of the angle.

Protractor postulate

The measure of an angle is equal to the absolute value of the difference between the real numbers matched with the two rays of the angle on a protractor.

Acute angle

Angle measures greater than 0˚ and less than 90˚.

Right angle

Measures 90˚.

Obtuse angle

Measures greater than 90˚ and less than 180˚.

Strait angle

Measures 180˚.

Angle addition postulate

m<abc = m<abm + m<mbc

Angle bisector

A ray that divides an angle into two congruent angles.

Complementary angles

Two positive angles whose measures have a sum of 90˚.

Supplementary angles

Two positive angles whose measures have a sum of 180˚.

Adjacent angles

Two angles that share a common vertex and side, but have no common interior points.

Linear pair

Two supplementary adjacent angles.

Vertical angles

Two angles whose sides form two pairs of oposite rays.

What you can conclude from a diagram.

• all points shown are coplanar

• points on a line are collinear

• a point that appears to be between two points is between two points

• lines that apear to intersect at a point intersect at a point

• angles that appear adjacent are adjacent

• angles that appear to be straight angles are straight angles

• a point that appears to be in the interior of an angle is in the interior of the angle

Regular polygons

Polygons with equal side lengths and equal angle measures

Trapezoid

A quadrilateral with exactly one set of parallel lines

Kite

Quadrilateral with two pairs of consecutive congruent sides

Parallelogram

Quadrilateral with two pairs of parallel sides

Rhombus

Equilateral parallelogram

Rectangle

Equiangular parallelogram

Square

Regular quadrilateral

Circle

The set of points in a plane a given distance from a given point

Radius

Distance between a point in the circle and the center point

Chord

A line segment whose endpoints lie on the circle

Diameter

The longest chord in a circle

Tangent

A line that intersects a circle at exactly one point

Congruent circles

Two or more circles with the same radius

Concentric circles

Two or more coplanar circles that share a center point

A circle is ________ about a polygon if and only if it passes through each vertex of the polygon. (The polygon is _________ in the circle)

Circumscribed, inscribed

A circle is __________ in a polygon if and only if it touches each side of the polygon at exactly one point. (The polygon is __________ about the circle)

Inscribed, circumscribed

Arc of a circle

Two points on a circle and a continuous part of the circle between the two points.

Semicircle

An arc of a circle whose endpoints are the endpoints of a diameter. It is named with three points.

Minor arc

An arc of a circle that is smaller than a semicircle.

Major arc

An arc of a circle that is bigger than a semicircle

Cylinder

Solid consisting of two congruent, parallel circular bases and the segments with an endpoint on each circle that are parallel to the segment between the centers of the circles.

Prism

A polyhedron with two congruent, parallel bases connected by lateral faces that are parallelograms

Sphere

The set of all points in space a given distance from a given point

Cone

A solid consisting of a circular base, a point nit in the plane of the circle, and all points on line segments connecting that point to points on the circle

Pyramid

A polyhedron consisting of a polygon base and triangular lateral faces that share a common vertex

Hemisphere

Half a sphere

What you cannot conclude from a diagram.

• unmarked lines are congruent

• unmarked angles are congruent

• angles that look like right angles are right angles

Space

The set of all points. Including those in the third dimension

Rigid transformations

A motion that produces a congruent image to the original image

Translation

• A slide

• a rigid motion

Rotation

• A turn

• a rigid motion

Reflection

• a flip

• a rigid motion

Deductive reasoning

Uses the laws of logic to find a true conclusion from two true premises

Law of syllogism

Conditional statement

A logical statement that has two parts, a hypothesis p, and a conclusion q. The statement is written if p then q.

Negation

The opposite of the original statement. The symbol is ~

Converse

Exchange the hypothesis and conclusion of a conditional statement

Inverse

The negation of the hypothesis and the conclusion

Contra positive

The inverse of the converse

Equivalent statements

When two statements are both true or both false

Perpendicular lines

Two lines that intersect to form a right angle

Biconditional statement

A statement that contains the phrase “if and only if”

Truth table

Used to determine the conditions under which a conditional statement is true

Counterexample

A specific case for which the conjecture is false

Law of detachment

If the hypothesis of a true conditional statement is true, then the conclusion is also true

Inductive reasoning

A way to write a conjecture based on a pattern found in specific cases

Two point postulate

Through any two points, there exists exactly one line.

Line-point postulate

A line contains at least two points

Line intersection postulate

If two lines intersect, then their intersection is exactly one point

Three point postulate

Through any three noncollinear points, there exists exactly one plane

Plane-point postulate

A plane contains at least three noncollinear points

Plane-line postulate

If two points lie in a plane, then their intersection line containing them lies in the plane

Plane intersection postulate

If two planes intersect, then their intersection is a line.

Line perpendicular to a plane

A line is ___________________ if and only if the line intersects the plane in a point and is perpendicular to every line in the plane that intersects it at that point.

Additional property of equality

If a = b, then a + c = b+c

Subtraction property of equality

If a=b, then a - c = b - c

Multiplication property of equality

If a = b, then a • c = b • c, c ≠ 0

Division property of equality