Thermofluids - Fluids

Steady and Un-Steady flow

steady: A steady flow is one in which the conditions (velocity, pressure and cross- section) may differ from point to point but DO NOT change with time.

unsteady: If at any point in the fluid, the conditions change with time, the flow is described as unsteady.

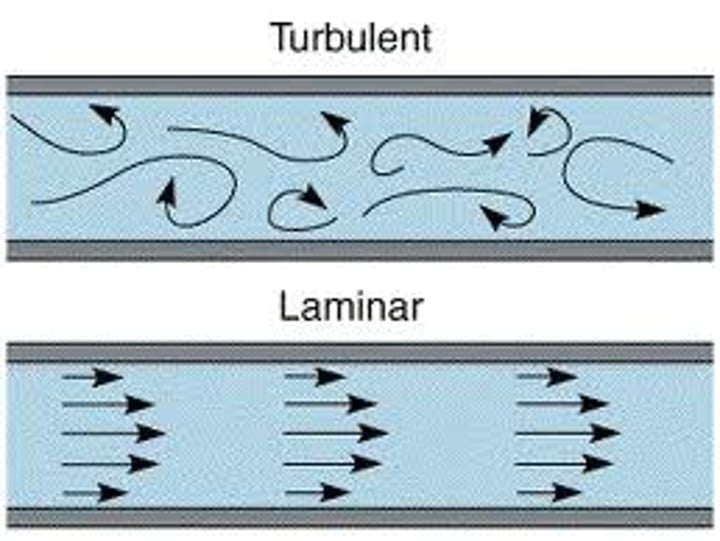
laminar and turbulent flow

Laminar flows are smooth and streamlined, whereas turbulent flows are irregular and chaotic. A low Reynolds number indicates laminar flow while a high Reynolds number indicates turbulent flow.

uniform and non-uniform flow

uniform: when the size and shape of cross section are constant along the length of channels under consideration

non-uniform: velocity is not constant at a given instant. A flow in which quantity of liquid flowing per second is not constant, is called unsteady flow.

compressible and incompressible flow

compressible flow: the density of the fluid does not remain constant.

incompressible: the density of the fluid remains constant

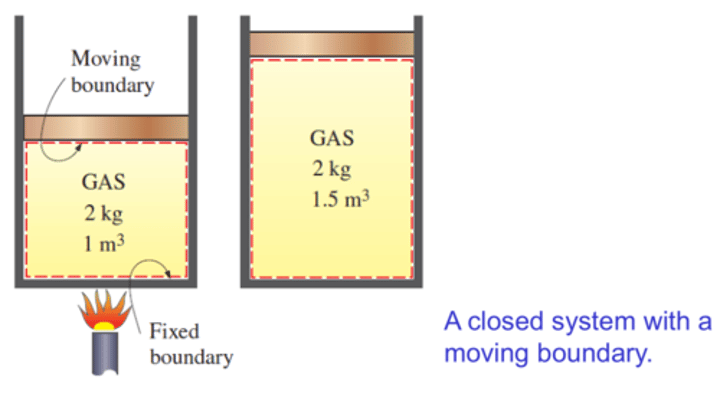
Control mass

a closed system that
contains a specific amount of mass.
Therefore mass can not pass across
the boundaries of a control mass.

Control volume

a selected region in space. It usually encloses
a region with flow in/out that we aim to study. Mass can cross
the boundaries of a control volume

extensive properties

depend on the size or extent of the system, e.g. total mass, total volume, total energy.

Intensive properties

are independent of the size of the system, but depend on the location in the system, e.g. temperature and pressure.

Shear Stress

The shear stress of a fluid can be defined as a unit area amount of force acting on the fluid parallel to a very small element of the surface. The greatest source of stress is the fluid viscosity.

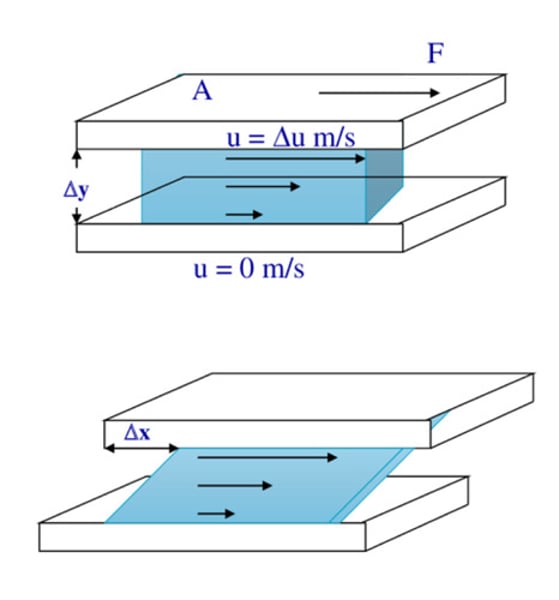
Shear stress formula

τ = μ*(du/dy)
where τ represents the shear stress, μ is the dynamic viscosity, du/dy is the velocity gradient perpendicular to the direction of shear.

Vicosity

a liquid's resistance to flow

Hydrostatic force

In a static fluid, pressure increases linearly with depth

Inside the water, pressure increases linearly with depth from Patm at the surface to Ptotal= Patm + ρgh at the base of the dam

Buoyant force

upward force a fluid exerts on an object

Fb = ρVg

Conservation of Mass

mass is conserved within a control volume for constant density fluids. total mass entering the control volume must equal the total mass exiting the control volume plus the mass accumulating within the control volume.

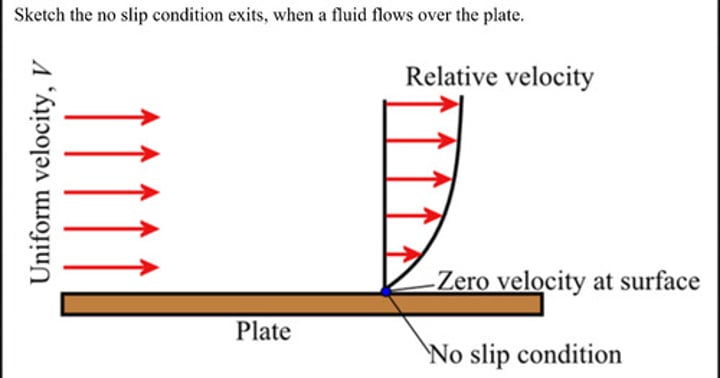
no-slip condition

a fluid that is in direct contact with a non-porous solid surface "sticks" to the surface. In other words, the fluid velocity (both tangential and normal) at the solid surface is zero.

mass flow rate (ṁ)

the amount of mass flowing through a cross section per unit time

ṁ = pVA
ṁ= m/t

volume flow rate

the volume of a fluid flowing through a cross section per unit time

V̇ = VA

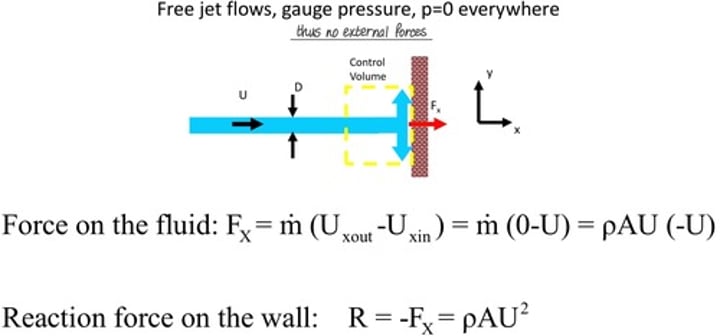
impact of a jet

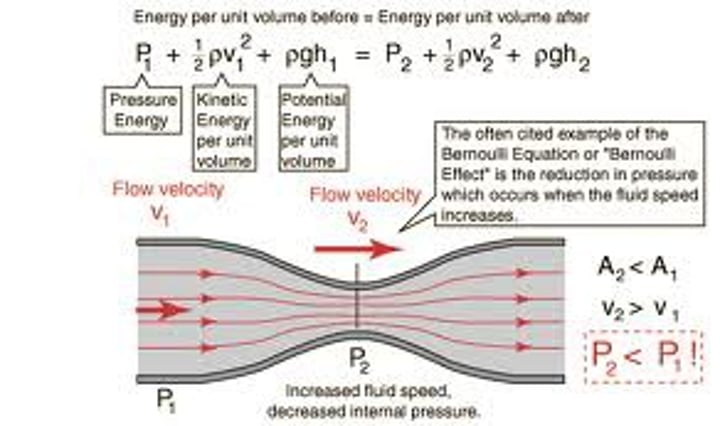
Bernoulli equation

energy equation along streamlines.
major assumptions:
1. Incompressible flow
2. There is no shaft work
3. There is one inlet and one outlet
4. The viscous friction is negligible
5. Negligible heat transfer

P1+1/2(ρv1^2)+ρgh1=P2+1/2(ρv2^2)+ρgh2

Reynolds number (Re)

Indicate whether fluid flow past a body or in a duct is steady or turbulent

Re = pVd/μ

Re < 2300 = Laminar flow
2300 < Re < 4000 = Transitional flow
Re > 4000 = Turbulent flow

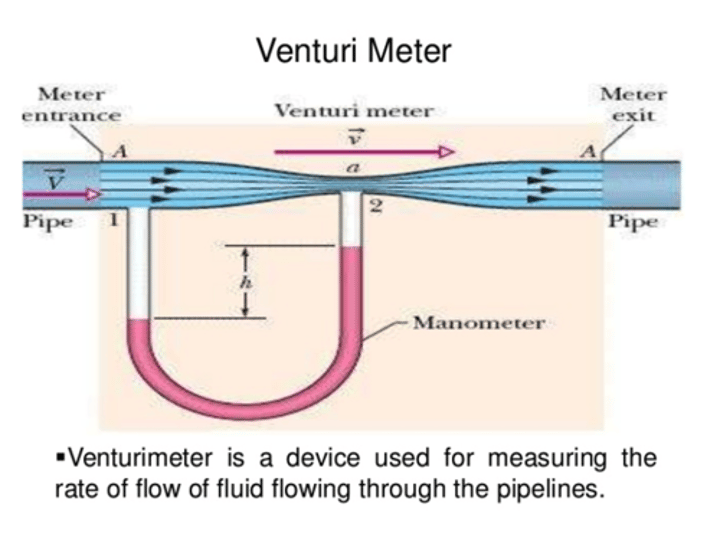
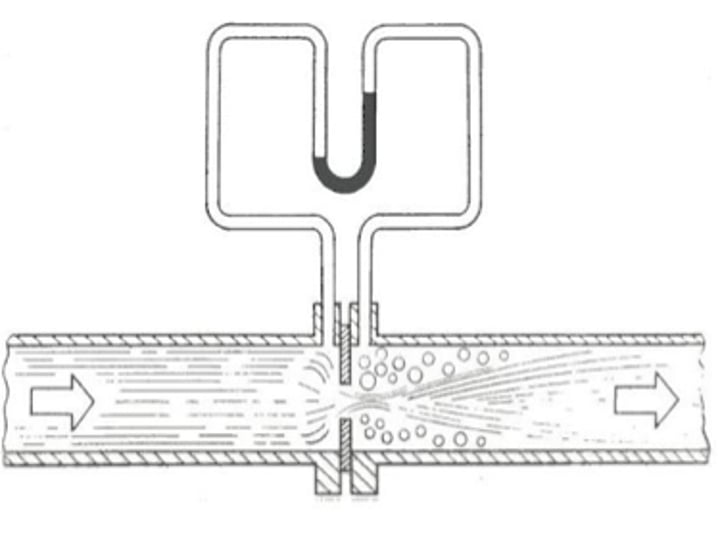
Venturimeter

Flow-measuring device used
for pipelines;
It consists of a tapered
convergent pipe section
followed by a slowly divergent
pipe section;
Pressure tappings at the meter
entry and the throat section.
These holes connect to a
manometer;
The downstream divergent
section is used to reconvert the
flow with minimal loss

Orifice Plate Meter

Orifice plate meter is less expensive and more compact but causes higher energy losses;
The pressure head loss is due to the turbulence generated as the jet diverges and is eventually transformed into heat.

Buckingham Π theorem

Step 1: List the parameters and count their total number n. Make sure that any listed independent
parameter is indeed independent of the others
Step 2: List the dimension of each parameter, and count the total number of primary dimensions j
(i.e. L, M, T, Θ) that construct the dimensions of parameters
Step 3: The expected number of Π's (i.e. the number of non-dimensional parameters) is k = n - j
Step 4: Choose j repeating parameters (from inputs) that will be used to construct each Π
Step 5: Generate the Π's one at a time by grouping the j repeating parameters with one of the remaining parameters, forcing the product to be dimensionless.

Boundary layer Development

Over a flat plate, initially the boundary layer is laminar
• As we move downstream, the boundary layer grows in size and at some point transition to turbulent takes place
• Over any solid surface, viscous forces are active up to a certain height δ away from the wall.
• That height δ is known as boundary layer thickness and the zone where viscous forces are important is boundary layer

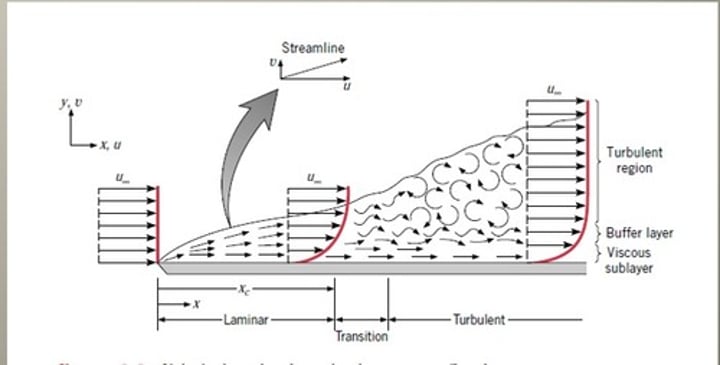
Re for Boundary layer

Reynolds number for flow across flat plate.

Re = pUx/μ

Drag (Fd) and Lift (Fl) coefficients

Drag
Fd = Cd ( 1/2(pAV^2) )

Lift
Fl = Cd ( 1/2(pAV^2) )

Pressure drag and viscous drag

viscous drag (friction drag)
cause: wall shear-stress distribution
flow physics: boundary layer around the object

Pressure drag
cause: pressure difference between the front and rear side of the object flow physics: boundary layer separation

Pressure drag vs viscous drag

Streamlining decreases the
pressure drag, but by making
the body longer so as to
promote a gradual increase in
pressure, the friction drag is
increased.
The optimum amount of
streamlining, then, is that for
which the sum of the friction
and pressure drag is a
minimum.

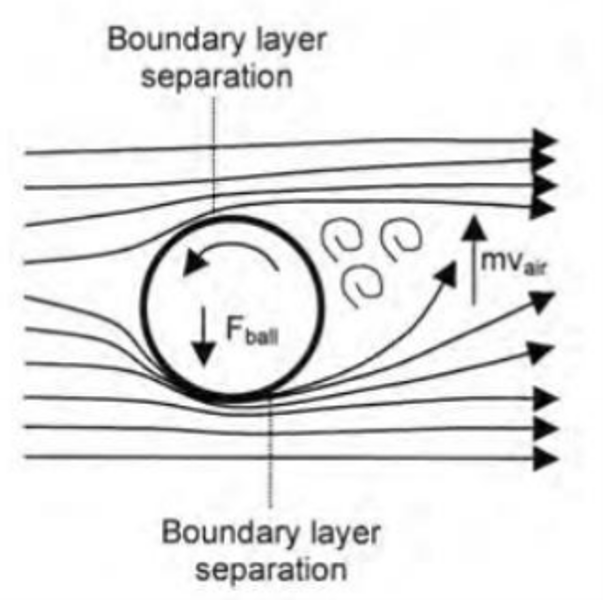
Boundary Layer Separation / Separation Point

Location of the separation point on a given curved surface will be
very different for laminar/turbulent boundary layer
Turbulent flow better withstands the adverse pressure gradient, with
the point of separation moving downstream

1D vs 2D vs 3D flow

1D flow occurs in a single dimension, typically represented by a straight line. 2D flow occurs in two dimensions, usually represented by a plane. 3D flow occurs in three dimensions, represented by a space or volume.

Gauge Pressure

the difference between the actual pressure and the atmospheric pressure

Pgauge = pgh - Patm