AP Pre-Calculus Concepts and Functions Unit 1-2

Sequence

A discrete set of points (not continuous) whose domain is whole numbers (0,1,2,3...)

Arithmetic Sequence

Terms have a common difference d and behave like linear functions.

Geometric Sequence

Terms have a common ratio r; to get ratio divide second term by first or divide third term by the second.

Exponential Functions

Functions of the form f(x) = ab^x where a > 0 and b > 1.

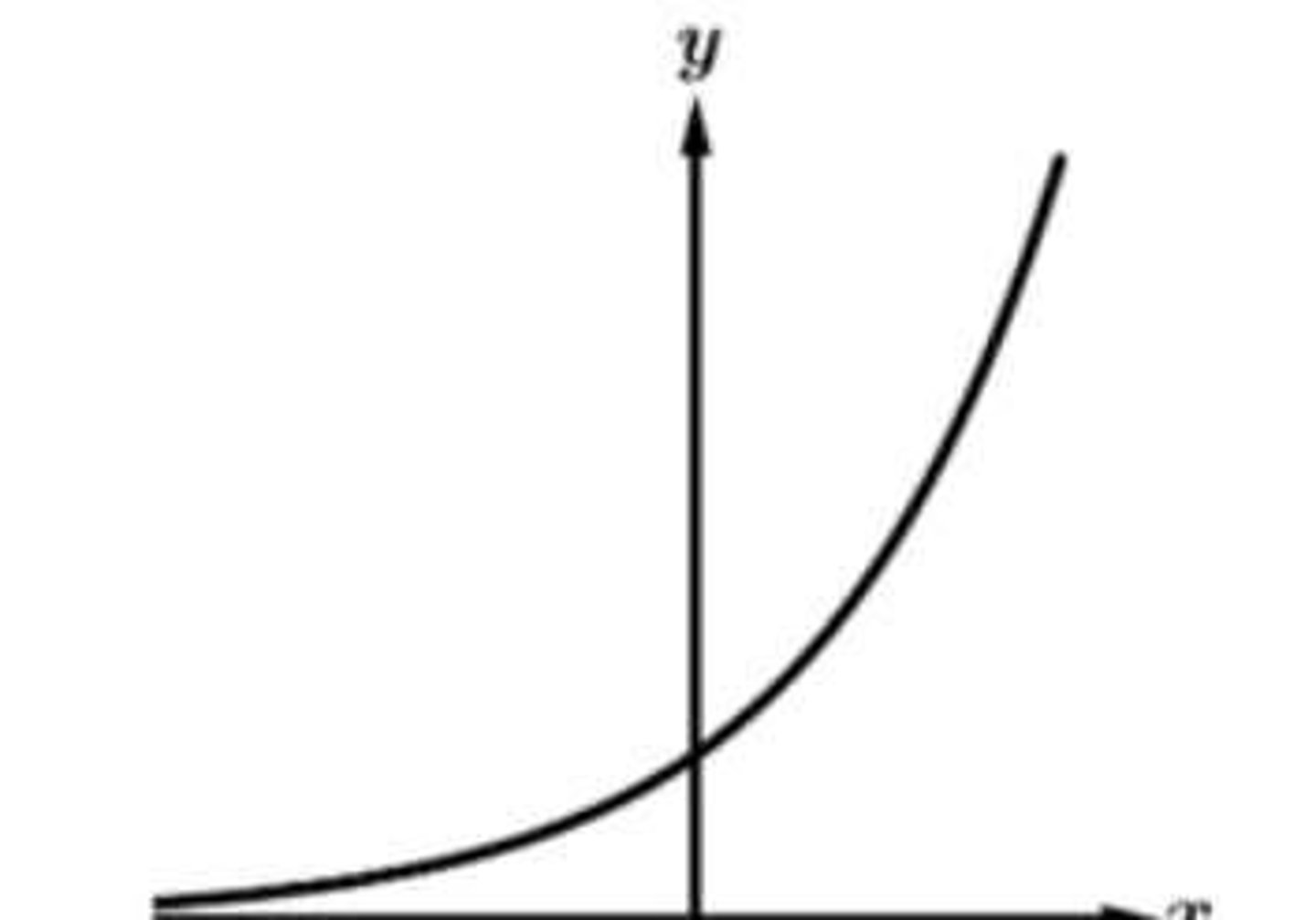
Exponential Growth

Always increasing or decreasing, with a horizontal asymptote y = 0 unless shifted vertically.

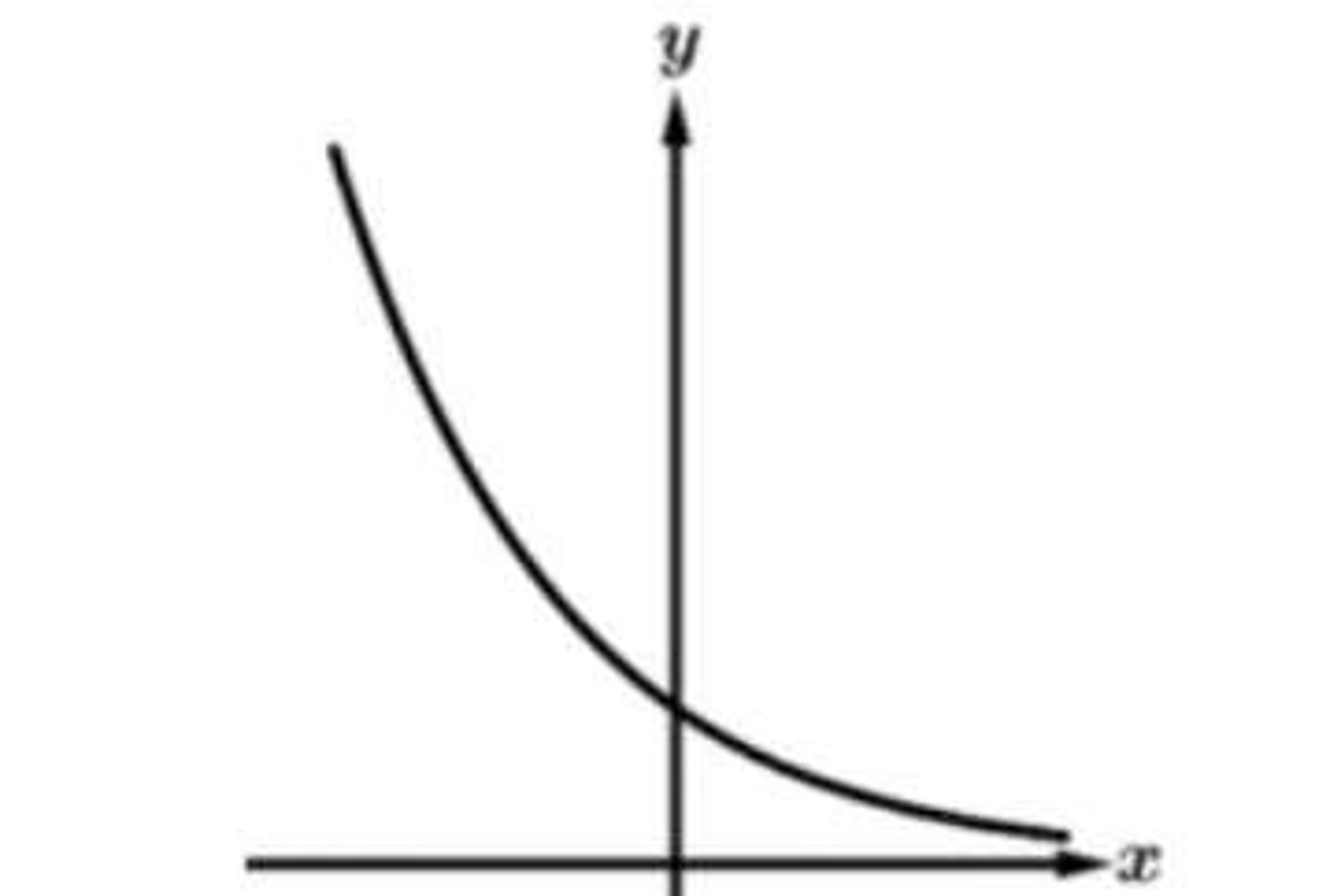
Exponential Decay

Functions of the form f(x) = ab^x where a > 0 and 0 < b < 1.

Exponent Rules

bm . bn = bm+n; (bm)n = bm.n; 1/bm = b-m; 1/bk = b-k.

Transformations of Exponential Functions

Reflections and translations will affect the graph.

Function Modeling

If the function has been vertically translated, you will not see the proportional difference; you will have to add/subtract a constant to see the proportional growth.

Residuals

Residual = Actual value - Predicted Value; if the residual is negative the predicted value is an over-estimate, if positive it is an under-estimate.

Composition of Functions

Combining two functions where the output of one function becomes the input of another.

Inverse Functions

Functions that reverse the effect of the original function.

Limit of Exponential Growth

lim f(x) = 0 as x → ∞.

Limit of Exponential Decay

lim f(x) = ∞ as x → 0.

Linear Function

A function with a constant rate of change.

Quadratic Function

A function with a constant second difference.

Exponential Function Characteristics

Inputs are linear, outputs are proportional.

Base of Exponential Growth

The base is larger than 1.

Base of Exponential Decay

The base is between 0 and 1.

Horizontal Translation

Every horizontal translation can be re-written as a vertical dilation.

Vertical Dilation

A change in the vertical stretch or compression of a graph.

Constant Rate of Change

The rate of change in a linear function.

Composite Function

f(g(x)) = (fog)(x)

Domain of g(x)

The domain for g(x) is x ≥ 0

Domain of f(g(x))

The domain for f(g(x)) is x ≥ 1

Composite Function Domain

The domain for the composite function is [0,1)U(1,∞)

Inverse Function Notation

Given a function f(x), its inverse is notated by f-¹(x)

Invertible Function

For a function to be invertible it must be one-to-one (pass the horizontal line test)

Inverse Function Graphs

Graphs of inverse functions are reflections over the line y = X

Domain and Range of Inverses

The domain and range of a function and its inverse are swapped.

Composition of Function and Inverse

The composition of a function and its inverse should equal x: ƒ (ƒ−¹(x)) = x

Finding Inverse Steps

1) Replace f(x) with y 2) Switch x and y 3) Solve for y

Logarithmic to Exponential Form

If log₁ c = a then bª = c

Base of Logarithm

If there is no base listed, the base is 10

Evaluating Logarithm

To evaluate a logarithm rewrite it in exponential form: Example log₂ 8 is rewritten as 2x = 8 which equals 3

Inverse of Exponential Functions

Logarithms are the inverse of exponential functions

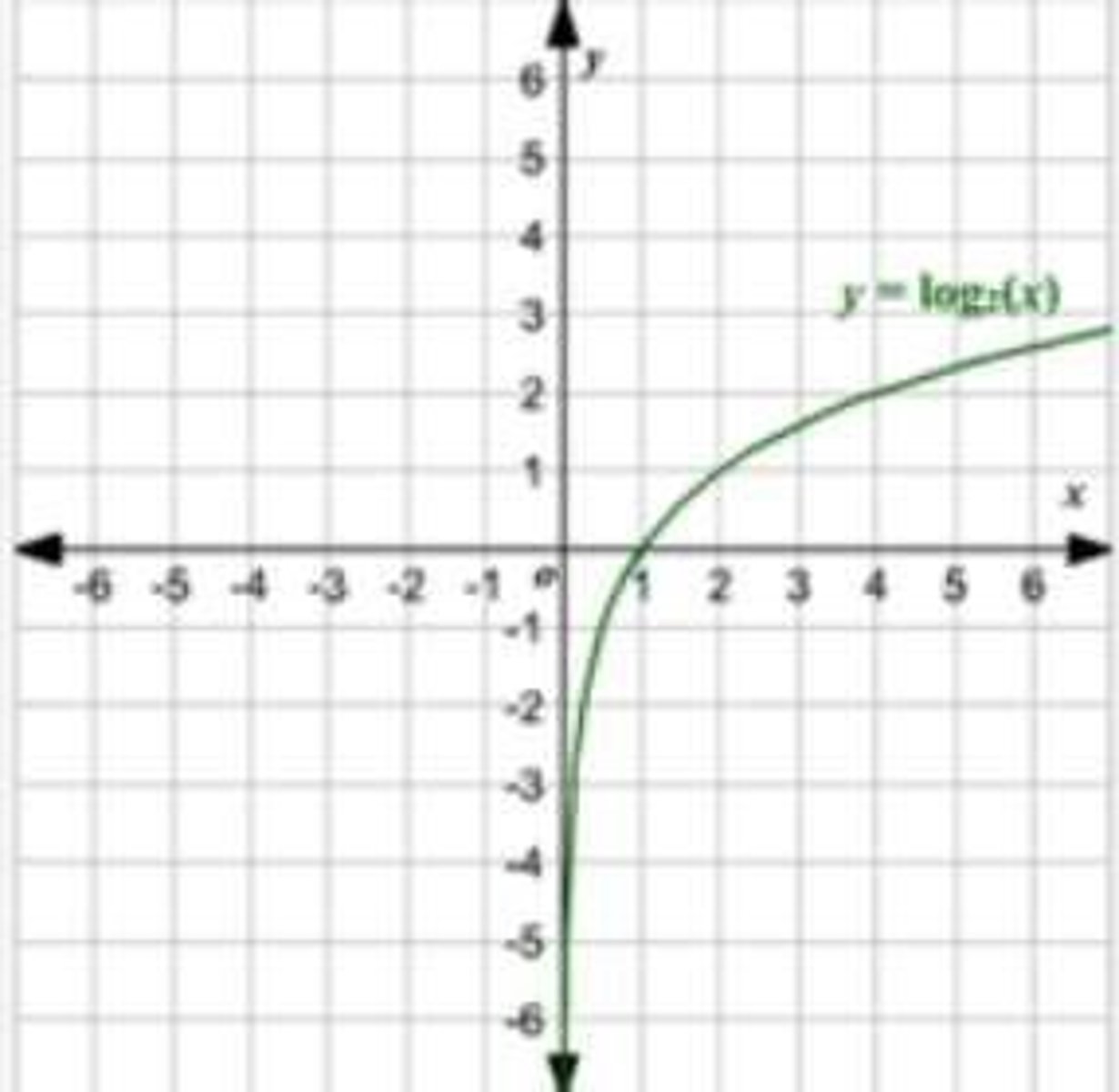
Composition of Functions

If f(x) = bx and g(x) = logb x then f(g(x)) = g(f(x)) = x

Domain of Exponential Functions

Domain of the exponential is the range of the logarithm.

Range of Exponential Functions

Range of the exponential is the domain of the logarithm.

Vertical Asymptote

Has a vertical asymptote x = 0

Logarithmic Data

Logarithmic data will have inputs that are proportional and outputs that are linear - Reverse of exponential data

Logarithmic Properties

logb (xy) = log₁ x + logb y

Change of Base Formula

Change of base = log₁x / loge

Solving Logarithmic Equations

Always check for extraneous solutions (Can't take the log of zero or a negative number)

Logarithmic Inequalities

Create a sign chart and determine if solution is in the domain of the given inequality

Exponential Function Linearization

Given f(x) = ab^x, the linearization of that function is logn y = logn b * x + logn a

Rate of Change

If the rate of change of a function is positive the graph is increasing. If the rate of change is negative the graph is decreasing. If the rate of change is increasing the function is concave up. If the rate of change is decreasing the function is concave down.

Average Rate of Change

The average rate of change visually is the slope of a secant line.

Instantaneous Rate of Change

The instantaneous rate of change visually is the slope of the tangent line.

Methods to Approximate Instantaneous Rate of Change

1. If given a table or equation pick two points close together and calculate slope. 2. If given a picture, draw a tangent line and approximate the slope of that line.

Rate of Change of Linear Function

The rate of change of a linear function is constant.

Rate of Change of Quadratic Function

The rate of change of a quadratic function is the second rate of change.

Point of Inflection

A point where the graph changes concavity.

Relative (local) Extrema

Extrema means maximums and minimums. Of all the relative extrema, the greatest y value is the absolute maximum and the least y value is the absolute minimum.

Absolute (global) Extrema

The absolute maximum is the greatest y value among all relative extrema, and the absolute minimum is the least y value.

Even Functions

Even functions are symmetric about the y-axis. Proof: f(-x) = f(x).

Odd Functions

Odd functions are symmetric about the origin. Proof: f(-x) = −ƒ(x).

Extrema on Closed Interval

On a closed interval, endpoints count as maximums and minimums.

Graph Changes from Increasing to Decreasing

The graph changes from increasing to decreasing at x = c.

Graph Changes from Decreasing to Increasing

The graph changes from decreasing to increasing at x = c.

Multiplicity of Zero

How the multiplicity of zero affects the graph.

Imaginary Solutions

Solutions that are not real numbers.

Degree of a Function

How to determine the degree of a function given a table.

Number of Solutions of a Polynomial

How to determine the number of solutions of a polynomial looking at the equation.

Conjugate

If 1 + i is a solution, so is its conjugate 1 - i.

Rate of Change

Keep finding the rate of change until it becomes constant; the degree will be how many times it takes for the rate of change to be constant.

Degree of Polynomial

The degree of the polynomial determines the number of zeros. Ex: A cubic function has three zeros.

Odd Multiplicity Zero

If a zero has an odd multiplicity, the graph will cross through the x-axis.

Even Multiplicity Zero

If the multiplicity of the zero is even, the graph will be tangent to the x-axis (bounce).

End Behavior of Polynomials

The behavior of the graph of a polynomial as x approaches positive or negative infinity.

Even Degree Polynomial

If a polynomial is of even degree, the ends of the graph will go in the same direction.

Rational Function End Behavior

The behavior of a rational function as x approaches positive or negative infinity.

Slant Asymptote

When the numerator is one degree higher than the denominator, there is a slant asymptote.

Limit Notation

lim f(x) = a as x approaches +∞.

Finding Zeros of Rational Functions

Set numerator equal to zero after factoring and simplifying (assuming there was no common factor that simplified).

Vertical Asymptote

x = a is a vertical asymptote.

Determining a Hole

Cancel out a common factor and the factor is either eliminated or remains in the numerator.

Vertical Asymptote Definition

After factoring and simplifying, the denominator equals zero.

Definition of a Hole

The limit from the left equals the limit from the right, but the function is not defined at the x-value.

Limit from the Left

lim_ f(x) as x approaches a from the left.

Limit from the Right

lim f(x) as x approaches a from the right.

Transformation of Functions

y = af(b(x + c)) + d.

Vertical Dilation

a = vertical dilation (affects y values).

Horizontal Dilation

b = horizontal dilation results in a dilation by a factor of (affects x values).

Horizontal Translation

c = horizontal translation (affects x values).

Vertical Translation

d = vertical translation (affects y values).

Calculator Skills

Approach the x value from the left and from the right.

Finding Max and Mins

Finding maximum and minimum values of a function.

Calculating Zeros

Finding the zeros of a function.