Electromagnetics Midterm 1 Flashcards

No curl is occurring if

the curl = 0

Divergence free curls are represented as

a constant

True or False: you cannot have curl without divergence

False

Negative divergence is when

the vector field is draining into a point

Positive curls are represented by

Curling towards the left (using the right hand rule, if your thumb points out at you, your fingers curl left in the positive direction

Positive divergence is when

the vector field is spread out from a point

Curl tells us

the direction/orientation of maximum possible circulation of the vector field

Curl takes in a _____ and spits out a _____

vector field, vector field

Divergence takes in a ____ and spits out a _____

vector field, scalar field

Gradient takes in a ____ and spits out a _____

scalar field, vector field

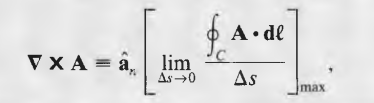
When dealing with curl, C is

the differential path that maximizes the circulation integral

Stokes’s theorem states that

The integral of the curl of a vector field across the surface of a vector field is equal to that of the flux integral of a vector dot producted with dl over the contour that bounds S in a right-handed sense

Electromagnetics is

the study of how electric charges and currents interact with each other

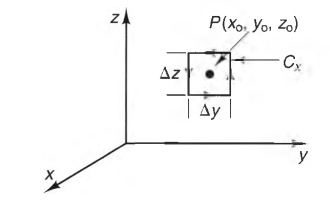
The position vector of a point is

defined as the directed distance from the origin to the point and is represented by the symbol r

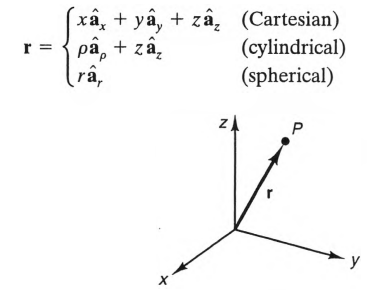
Position vector foreach coordinate systems (r = ? )

Cartesian: xa^x + ya^y + za^z

Cylindrical: pa^p + za^z

Spherical: ra^r

What is R?

the directed distance between two arbitrary points

The rate at which a scalar changes close to a point is

gradient of

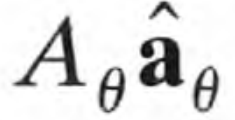
Define and contrast theta and base vector theta

Theta is a coordinate and scalar, and ace of theta is a base vector that points in increasing values of theta and has a magnitude of 1 and constant values of fi and r.

Vector analysis is

the branch of mathematics that was developed to describe quantities that are both directional in nature and distributed over regions of space

The definition of a physical quantity is

the description of the operational procedure used to measure it

Discrete quantities are

defined over regions of space or at single points, but not on a point-by-point basis throughout a region.

Field quantities are

defined on a point-by-point basis throughout a region of space

A scalar is

a quantity that can be specified by a single number and its associated unit

A vector is

a quantity that can be specified by a magnitude and a direction.

The directed distance Rab between the points a and b is

a vector whose magnitude equals the distance between these points and whose direction is parallel to the line directed from a to b

What does the dot product tell us?

Two vectors A and B are perpendicular (or orthogonal) if A • B = 0. Vectors are collinear it |A • B| = |A | |B|. Collinear vectors are parallel if A • B = |A| |B| and are antiparallel if A • B = - |A| |B |.

The position vector is

the directed distance of point P from the origin & is represented by symbol r

How many components does the position vector r of an arbitrary point P have when represented in the spherical coordinate system?

r has just one component in the spherical coordinate system

What does dv represent?

A small volume at a point in space

What does ds represent?

A small surface at a point in space

What does dl represent?

A small length of a line

What does dl represent?

“A small piece/stop of a path between P1 and P2” Also is a vector quantity

________ have coordinates

Coordinate systems

________ have components

r , the position vector

A certain vector field B( r ) is completely represented by the expression:

B( r ) = 4(a^r) + 2(a^theta) - 6(a^fi)

What is the expression for Br?

What is the value of theta?

“Br = 4

Theta is unknown”

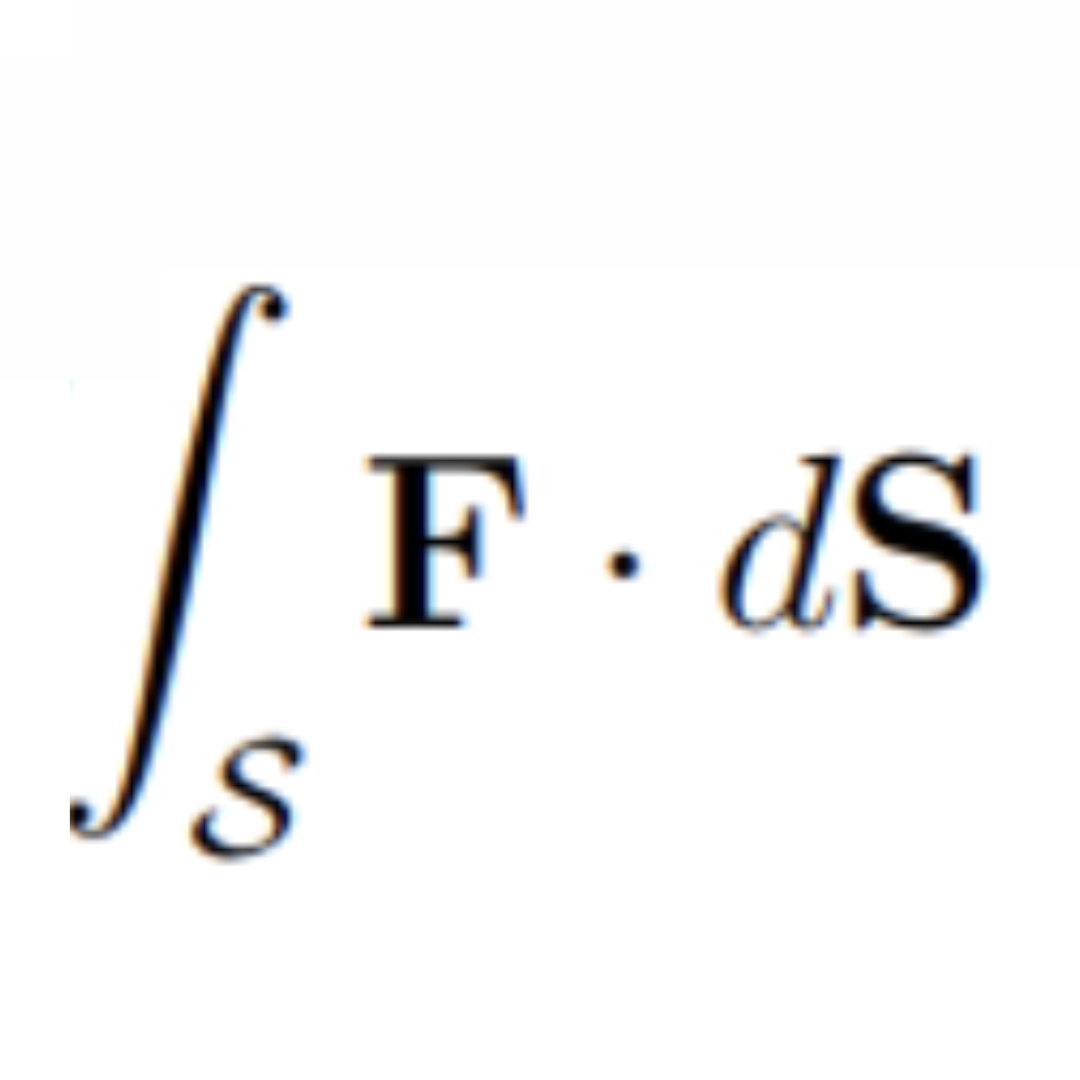
For the integral in the image, S is some surface, and F represents the air velocity (mag. and direction) over a region of space. How might the value of the integral be intepreted?

The integral is the rate of air flowing through S

The gradient has nothing to do with

A volume or a surface

The divergence of a ________ is a ___________

vector field, scalar field

A surface is closed if there is

an inside and an outside

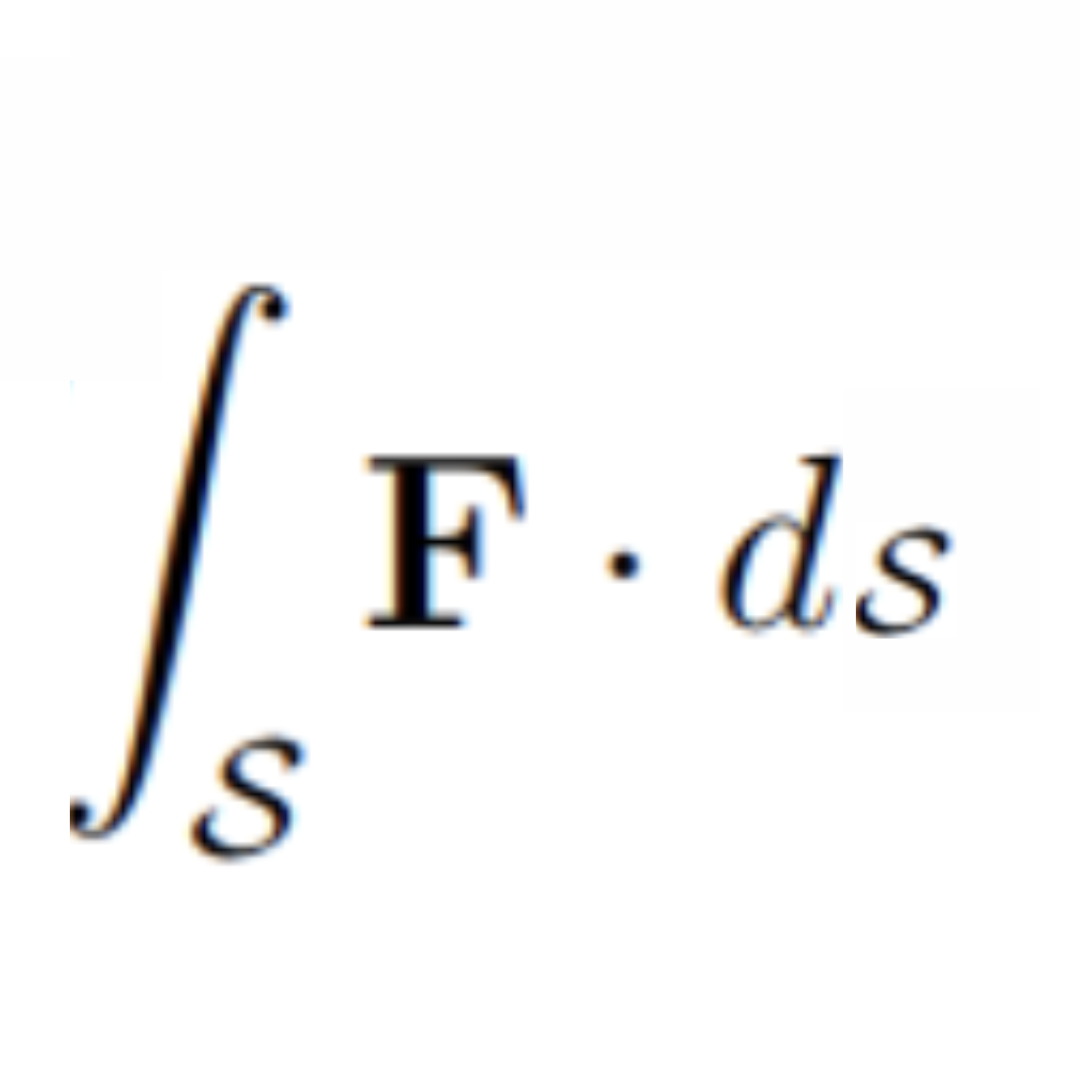
What is this integral trying to find?

We are trying to find the average of the force F across the surface, S, and we only care about area and NOT orientation

Solving for the “net leakage internally” is equivalent to solving for:

“The net leakage at the surface”

What does the cross product of two vectors tell us?

It tells us a vector that is perpendicular to that of the two other vectors

Divergence:

measures the tendency of a vector field to collect or disperse at a point

Thus, the gradient del f:

is a vector that points in the direction of maximum rate of increase of the function f