Unit 1: Limits and Continuity

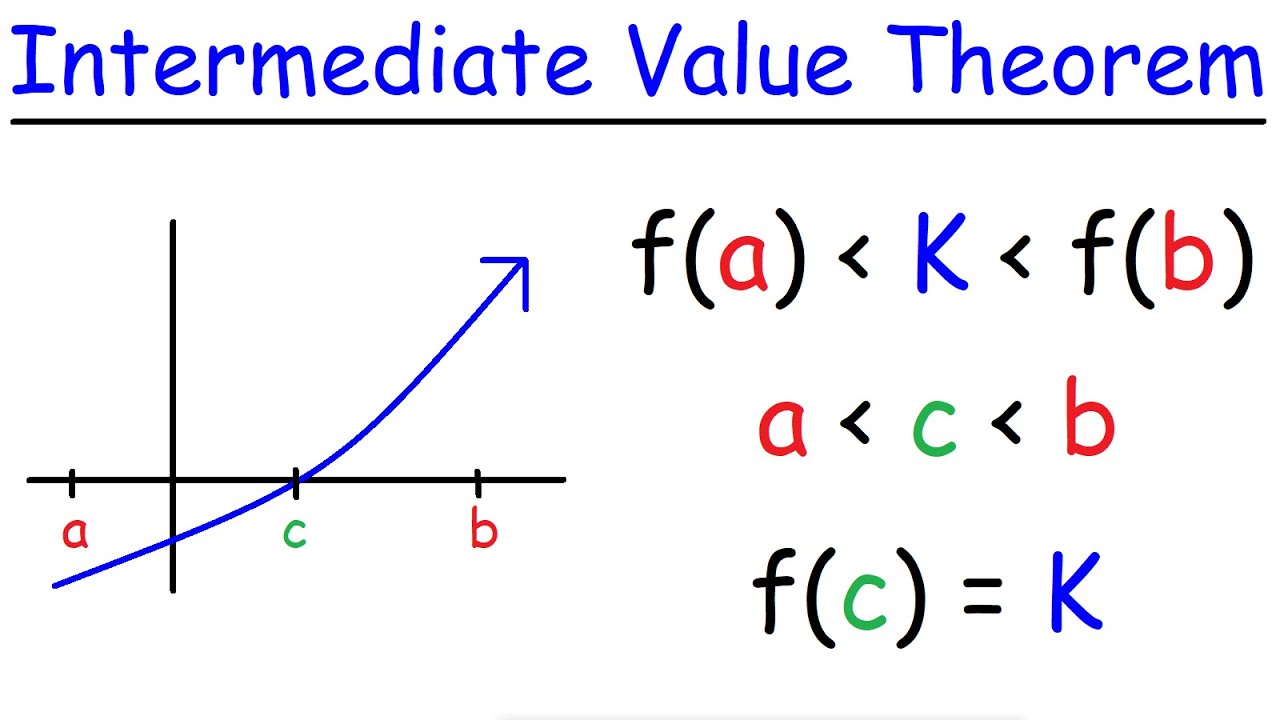
IVT Theorem

If f is a continuous function whose domain contains the interval [a, b], then it takes on any given value between f(a) and f(b) at some point within the interval.

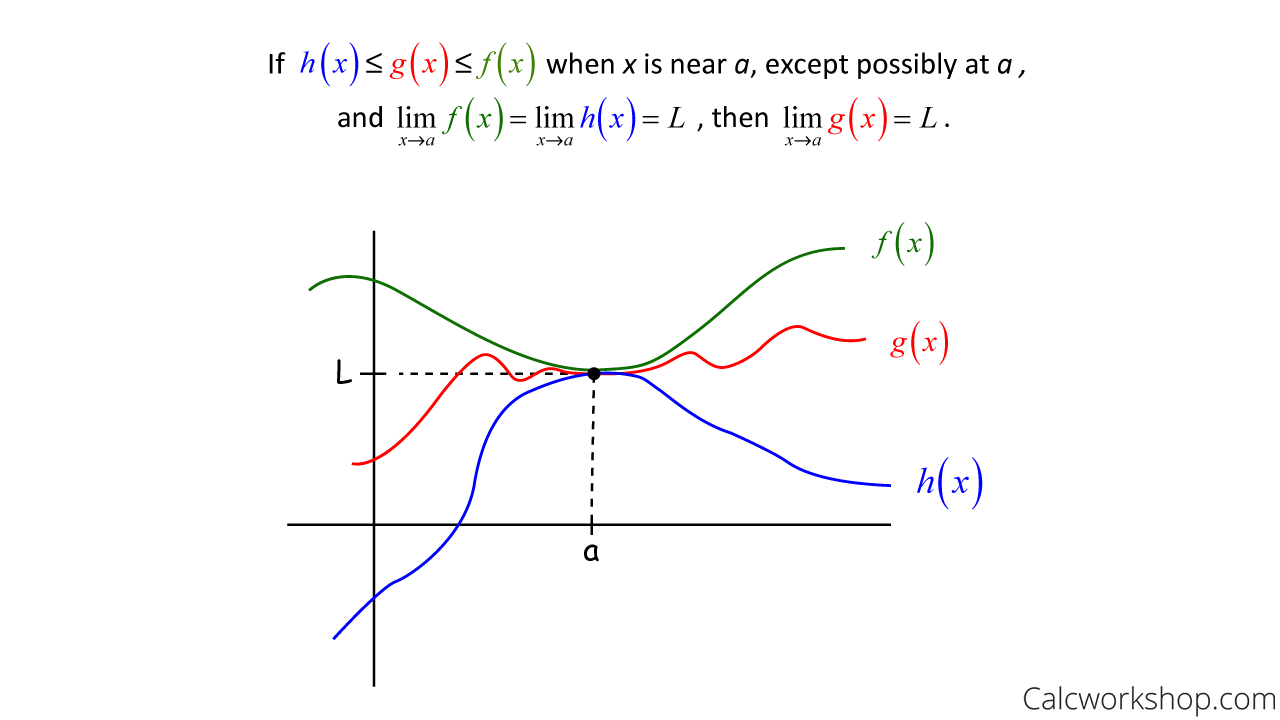
Squeeze Theorem

If f(x) ≤ g(x) ≤ h(x) for all x in an interval, and lim(x→c) f(x) = lim(x→c) h(x) = L, then lim(x→c) g(x) = L.

Continuity

1. f(c) exists

2. lim(x→c) f(x) exists

3. lim(x→c) f(x)=f(c)

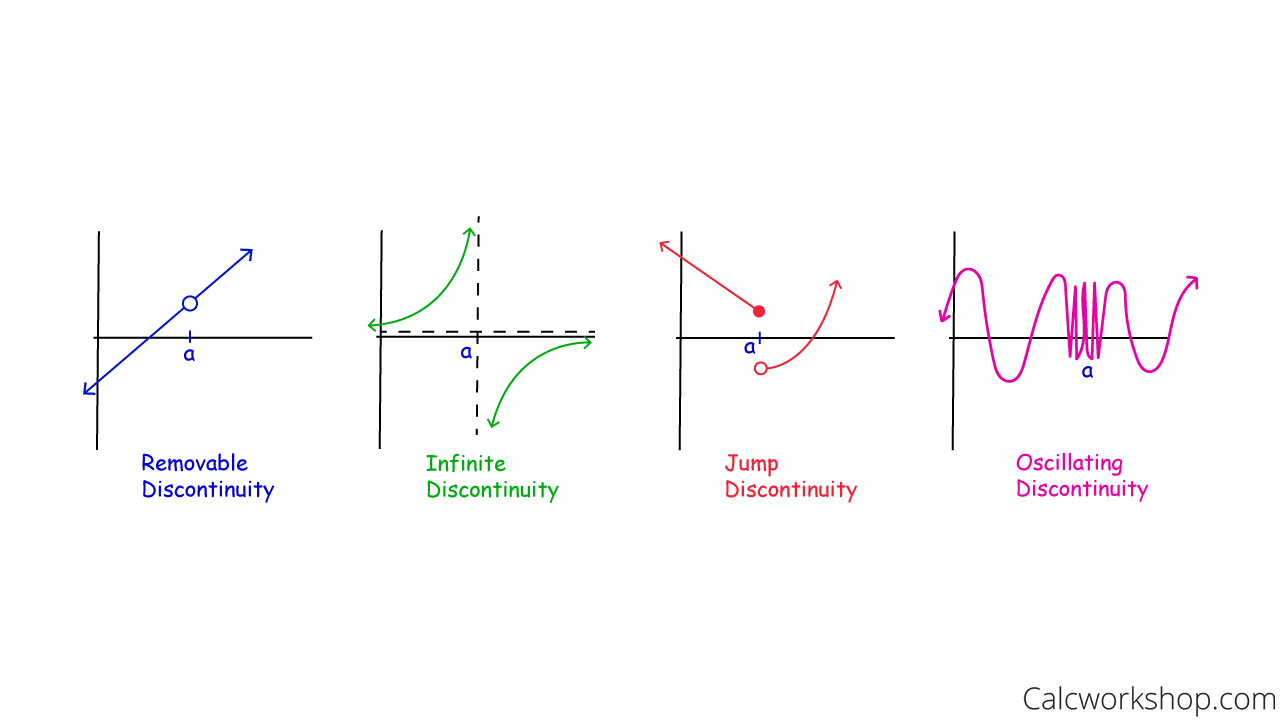
Types of Continuities

• Point Discontinuity is also called a Removable Discontinuity

• Jump, Infinite, and Oscillating Discontinuities are a Non-Removeable Discontinuity

lim(x→∞) m>n

lim=DNE, will be either +∞ or -∞

no H.A,

lim(x→∞) m=n

Limit and H.A. is the ratio of the leading co-effecients

y=a/b

lim(x→∞) m<n

Limit and H.A. are equal to 0

y=0

#/∞= ?

#/∞=0

∞/#= ?

∞/#= ∞

∞*∞= ?

∞*∞= ∞

Rate of Change

constant < lnx < x^n < e^x < x^x

Is a polynomial always continuous?

Yes